Тема 1.10. Сложное движение точки.

1.10.1. Абсолютное, относительное и переносное движение точки.

1.10.1. Теорема сложения скоростей.

1.10.1. В Теме 1.7. (Основные понятия кинематики) мы уже говорили, что всякое движение тела или точки есть движение относительное, т.е. его можно наблюдать и изучать лишь по отношению к другим физическим телам и связанным с ними системам отсчёта. В предыдущих темах мы рассматривали движение по отношению к так называемой «неподвижной» системе, за которую в технической практике принимают обычно систему отсчета, жестко связанную с Землей.

Движение точки по отношению к системе отсчета, принимаемой за неподвижную, называется абсолютным дви­жением.

В ряде случаев движение точки по отношению к не­подвижной системе отсчета бывает удобно рассматривать как движение сложное, состоящее из двух одновременных движений: движения точки по отношению к некоторой подвижной системе отсчета и движения точки вместе с подвижной системой отсчета по отношению к неподвижной.

Так, например, движение какой-либо точки М колеса автомобиля (рис. 1.10.1.), совершающееся по отношению к Земле по кривой, называемой циклоидой, можно считать состоящим из двух простых движений: движения точки по окружности по отношению к корпусу автомобиля и дви­жения этой точки вместе с поступательно движущимся корпусом автомобиля.

Движение точки по отношению к подвижной системе отсчета называется относительным движением.

Движение подвижной системы отсчета и всех неизмен­но связанных с ней точек по отношению к неподвижной системе отсчета называется переносным движением.

Чтобы определить переносное движение какой-либо точки в данный момент времени, надо мысленно прекра­тить относительное движение данной точки и определить ее движение вместе с подвижной системой отсчета по от­ношению к неподвижной системе отсчета. Аналогичным приемом бывает иногда удобно пользо­ваться и для выяснения относительного движения точки. Чтобы его определить, надо мысленно прекратить пере­носное движение точки.

В приведенном выше примере круговое движение точки М по отношению к движущемуся корпусу автомобиля есть, очевидно, относительное движение. Если эту точку мысленно неизменно связать с корпусом автомобиля, то ее движение вместе с ним будет переносным движением. Движение же точки М (по циклоиде) по отношению к Земле—абсолютное дви­жение.

Приведем для поясне­ния еще один при­мер. Движение человека по палубе движущегося по реке парохода есть дви­жение относительное. Дви­жение точки палубы паро­хода, в которой в дан­ный момент находится че­ловек, относительно бере­га реки—переносное дви­жение, а движение челове­ка относительно берега — абсолютное движение.

Условимся обозначать абсолютную скорость точки принятым ранее символом 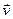, а относительную и перенос­ную скорости тем же символом, но с соответствующими подстрочными индексами: отн — для относительного дви­жения ( 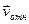) и пер—для переносного движения ( ).

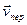Абсолютной скоростью 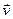данной точки называется ее скорость по отношению к неподвижной системе отсчета.

Относительной скоростью 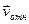данной точки называ­ется ее скорость по отношению к подвижной системе отсчета.

Переносной скоростью 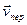какой-либо точки М называется абсолютная скорость той неизменно связанной с подвижной системой точки, с которой совпа­дает в этот момент данная точка М.

Так. как только при поступательном движении под­вижной системы отсчета скорости всех связанных с ней точек одинаковы, то лишь в этом случае переносная скорость движущейся точки не зависит от ее положения относительно подвижной системы отсчета и под ней в этом случае можно понимать скорость подвижной систе­мы отсчета относительно неподвижной.

1.10.2. Теорема сложения скоростей.Абсолютная скорость точки равна гео­метрической сумме ее переносной и относительной ско­ростей:

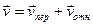
Так как при геометрическом сложении двух скоростей точки ее ре­зультирующая скорость изображается диагональю параллелограмма, по­строенного на составляющих скоростях как на сторонах, то данную теорему называют часто правилом параллелограмма.

Если модули переносной 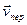и относительной 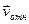скоростей точки и угол 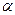между их направлениями из­вестны, то модуль абсолютной скорости находится на основании теоремы косинусов (совершенно так же, как и при сложении двух сил, приложенных к одной точке):

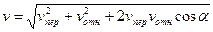
Вопросы для самопроверки.

1. Дайте определение абсолютного, относительного и переносного движения точки.

2. Что называется абсолютной, относительной, переносной скоростью точки?

3. Сформулируйте теорему о скорости точки в сложном движении.