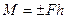Тема 1.3. Момент силы относительно точки. Пара сил.
1.3.1. Момент силы относительно произвольной точки. Теорема Вариньона.
1.3.2. Пара сил. Момент пары сил.
1.3.3. Свойства пары сил. Условие равновесия пар.
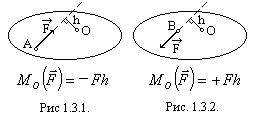 1.3.1. Сила, действующая на тело, может не только смещать его, но и поворачивать вокруг какой-нибудь точки. Пусть сила
1.3.1. Сила, действующая на тело, может не только смещать его, но и поворачивать вокруг какой-нибудь точки. Пусть сила 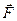 , приложенная в точке А, стремится повернуть тело вокруг точки О (рис. 1.3.1.). Поскольку силу можно переносить по линии её действия, то вращательный эффект этой силы не будет зависеть от того, в какой точке эта сила приложена, а будет зависеть от значения самой силы и от расстояния
, приложенная в точке А, стремится повернуть тело вокруг точки О (рис. 1.3.1.). Поскольку силу можно переносить по линии её действия, то вращательный эффект этой силы не будет зависеть от того, в какой точке эта сила приложена, а будет зависеть от значения самой силы и от расстояния 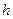 от точки О до линии действия силы. Расстояние
от точки О до линии действия силы. Расстояние 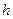 называется плечом силы
называется плечом силы 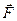 .
.
Моментом силы 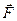 относительно произвольной точки (центра) О называется величина, равная произведению модуля силы
относительно произвольной точки (центра) О называется величина, равная произведению модуля силы 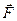 на её плечо
на её плечо 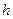 относительно точки О и взятая с соответствующим знаком:
относительно точки О и взятая с соответствующим знаком:
|
(1.3.1.)
Условимся считать, что момент имеет знак «плюс», если сила стремится повернуть тело вокруг центра О против часовой стрелки (рис. 1.3.2.), а знак «минус» - если по ходу часовой стрелки (рис. 1.3.1.).
Момент силы имеет, очевидно размерность силы, умноженной на длину:
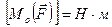 .
.
Момент силы характеризуется следующими свойствами:
1) при переносе точки приложения силы вдоль её линии действия момент силы не изменяется;
2) момент силы относительно данного центра равен нулю тогда и только тогда, когда сила равна нулю или плечо равно нулю (линия действия силы проходит через центр);
3) если плоская система сил 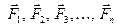 имеет равнодействующую
имеет равнодействующую 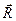 , то момент равнодействующей относительно любой точки плоскости действия сил равен алгебраической сумме моментов составляющих сил относительно той же точки (теорема Вариньона):
, то момент равнодействующей относительно любой точки плоскости действия сил равен алгебраической сумме моментов составляющих сил относительно той же точки (теорема Вариньона):

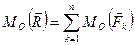 . (1.3.2.)
. (1.3.2.)
1.3.2. 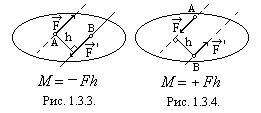 Особое место среди параллельных сил занимают две силы, равные по величине, но направленные в противоположные стороны (рис. 1.3.3.). Особенность заключается в том, что такая система сил не имеет равнодействующей (не может быть уравновешена одной силой ) и не находится в равновесии. Такая система двух параллельных сил
Особое место среди параллельных сил занимают две силы, равные по величине, но направленные в противоположные стороны (рис. 1.3.3.). Особенность заключается в том, что такая система сил не имеет равнодействующей (не может быть уравновешена одной силой ) и не находится в равновесии. Такая система двух параллельных сил 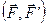 , равных по модулю и противоположных по направлению (
, равных по модулю и противоположных по направлению ( 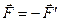 ) , называется парой сил или просто парой..
) , называется парой сил или просто парой..
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Расстояние 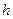 между линиями действия сил пары называется плечом пары.
между линиями действия сил пары называется плечом пары.
Пара сил, действуя на твёрдое тело, стремится сообщить телу вращательное движение, если этому не препятствуют наложенные на тело связи. Вращательный эффект пары зависит от модуля её сил и длины плеча, на котором действуют эти силы. Для характеристики этого эффекта вводится понятие момента пары, численное значение которого равно произведению модуля одной из сил пары на её плечо:
|
(1.3.3.)
Момент пары будем считать положительным, когда пара стремится повернуть тело против часовой стрелки (рис. 1.3.4.), а отрицательным -по ходу часовой стрелки (рис. 1.3.3.).
Момент пары сил имеет единицу силы, умноженной на длину:
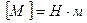 .
.
Действие пары на тело зависит от: 1) абсолютного значения момента пары, 2) положения в пространстве плоскости действия пары, 3) направления вращения пары в плоскости её действия.
1.3.3. Свойства пар характеризуются следующими тремя теоремами.
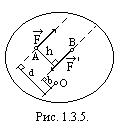 Теорема 1.Алгебраическаявеличина момента пары равна сумме алгебраических величин моментов сил, составляющих пару, относительно любой точки, лежащей в плоскости действия данной пары сил (рис. 1.3.5.):
Теорема 1.Алгебраическаявеличина момента пары равна сумме алгебраических величин моментов сил, составляющих пару, относительно любой точки, лежащей в плоскости действия данной пары сил (рис. 1.3.5.):
.
Теорема 2.Всякую пару, не изменяя её действия на абсолютно твёрдое тело, можно заменить другой парой, расположенной как угодно в той же плоскости и имеющей одинаковую с данной парой алгебраическую величину момента.
Следствия 1. Данную пару можно переносить куда угодно в плоскости действия пары, не изменяя оказываемого ею на тело действия.
2.У данной пары, не изменяя оказываемого на тело действия, можно произвольно менять модули сил или длину плеча, сохраняя неизменным момент.
Необходимо отметить, что перенос пары в её плоскости действия применим лишь для абсолютно твёрдого тела и используется при решении задач теоретической механики. Мы можем пользоваться этим свойством пары при решении задач на равновесие внешних сил, приложенных и к деформируемому телу, так как это равновесие не нарушается от того, что такое тело станет абсолютно твёрдым (принцип отвердевания, см. п. 1.1.3.) Но деформация тела и возникающие в результате её в теле внутренние силы, противодействующие этой деформации, зависят от места расположения пары, и потому в задачах сопротивления материалов всегда указывают сечение тела, на которое действует пара.
Поскольку в теоретической механике действие пары на тело вполне определяется её моментом, то в задачах обычно задают момент пары, а не модуль сил пары и плечо. При этом часто пару сил изображают стрелкой, показывающей направление вращения, не изображая ни сил пары, ни её плеча, а только указывая момент.
Теорема 3.Несколько пар, лежащих в одной плоскости, можно заменить одной результирующей парой, момент которой равен алгебраической сумме моментов составляющих пар.
Из теоремы 3 следует, что для равновесия пар , расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов всех данных пар равнялась нулю, т.е. условием равновесия пар является равенство
.
Вопросы для самопроверки.
1. Как определяется момент силы относительно точки?
2. Изменится ли момент силы, если силу перенести вдоль линии её действия?
3. В каком случае силы различной величины дают относительно одного и того же центра равные по величине моменты?
4. Что такое момент пары? Чем измеряется момент пары?
5. Какие пары называются эквивалентными?
6. Как найти пару, уравновешивающую данную плоскую систему пар?
Дата добавления: 2015-09-02; просмотров: 2333;

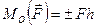 .
.