Вычисление коэффициента линейной корреляции
| № группы | Уровень успеваемости | Уровень удовлетво–ренности | (x- 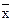 ) )
| (y– 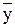 ) )
| (x– 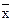 )(y– )(y– 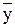 ) )
| (x– 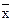 )2 )2
| (y– 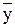 )2 )2
| ||||
| 4,04 | 2,3 | 0,22 | 0,27 | 0,0594 | 0,0484 | 0,0729 | |||||
| 4,03 | 2,33 | 0,21 | 0,27 | 0,0567 | 0,0441 | 0,0729 | |||||
| 3,57 | 1,75 | –0,25 | –0,28 | 0,0700 | 0,0625 | 0,0784 | |||||
| 3,64 | 1,80 | –0,18 | –0,23 | 0,0410 | 0,0324 | 0,0529 | |||||
| Итого | 15,28 | 8,15 | – | – | 0,2271 | 0,1874 | 0,2771 | ||||
| В среднем | 3,82 | 2,03 | – | – | – | – | – |
Подставим полученные данные в формулу вычисления коэффициента линейной корреляции:
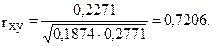
Квадрат линейного коэффициента корреляции – коэффициент детерминации – выражает объясняемую вариацию между признаками.
Существуют и другие коэффициенты парной корреляции, выбор которых зависит от того, в какой шкале измерены признаки.
Коэффициенты парной статистической взаимосвязи могут быть использованы и в том случае, когда признаки представлены в разных шкалах измерения. Признак в шкале более высокого уровня измерения рассматривается при этом как признак в шкале более низкого уровня измерения, соответствующий другому признаку (шкалы высокого уровня – количественные; среднего – шкалы порядка, ранговые шкалы; низкого – номинальные). Но при этом теряется определенная информация. Поэтому целесообразнее использовать статистические критерии различия групп объектов по признаку. Критерием значимости в этом случае является степень, в которой группы объектов, выделенные по одному признаку, например х, различаются по другому, например у.
Если х – номинальный дихотомический признак (пол, партийность), а у количественный (например, время, уделяемое тому или иному занятию), для оценки значимости может быть использован t-критерий. Чем больше (по абсолютной величине) значение t-критерия, тем более тесная взаимосвязь между признаками. Признак х можно считать значимым, если различия между двумя группами объектов по признаку у являются статистически значимыми. Проверка гипотезы и статистической значимости осуществляется на основе статистических таблиц. Если признак имеет больше двух значений, можно использовать F-критерий. Если у – порядковый, а х – номинальный, могут быть применены статистические критерии различия между группами объектов по порядковому признаку. Если у – номинальный, а х – количественный или порядковый, для оценки значимости х критерии t, F используются с переменой мест x и y [6].
Применение коэффициентов корреляции возможно только при условии однородности исследуемой совокупности.
Известным недостатком коэффициентов статистической взаимосвязи между парами признаков является то, что эта взаимосвязь может быть результатом некоторых других скрытых признаков. Поэтому использование коэффициентов парной статистической взаимосвязи требует определенной осторожности.
Недостаток корреляционного анализа позволяет преодолеть метод факторного анализа. Исследуемая совокупность характеризуется большим количеством признаков. Переход от некоторого числа легко измеряемых признаков изучаемого явления к относительному числу стоящих за ними скрытых, внешне ненаблюдаемых факторов или комбинаций признаков, – главная задача факторного анализа.
Факторный анализ обычно выполняется в 4 этапа.
Первыйэтап. Вычисляется корреляционная матрица для всех признаков, включенных в факторный анализ. Признаки должны быть однородными, относиться к одному и тому же изучаемому явлению. Если корреляция между двумя признаками слабая, маловероятно, что они образуют общий фактор.
Второй этап. Определяется число факторов, описывающих данные, и метод их вычисления.
Третий этап. Ротация, фокусирование преобразованных факторов для удобного их интерпретирования.
Четвертый этап. Выделяются факторные нагрузки для каждого отдельного признака в выделившейся группе признаков.
Любой признак можно представить в виде суммы некоторых других признаков, умноженных на свой коэффициент. Эти признаки принято называть факторами, а коэффициенты – факторными нагрузками. Содержательной интерпретации подвергается матрица факторных нагрузок. Те из них, которые относятся к одному фактору, располагаются в порядке убывания абсолютных значений. Рассматриваются нагрузки, имеющие максимальные абсолютные значения факторных нагрузок. Далее выявляется общее содержание этой группы параметров (общее свойство), которое, по мнению исследователя, объединяет признаки в одну группу. Это свойство или группа свойств называется фактором.
При проведении факторного анализа основных жизненных ценностей у молодежи в 1989 г. учащимся техникумов был представлен список из следующих ценностей:
1. Творчество
2. Учеба
3. Любовь
4. Фирменные вещи
5. Деньги
6. Уважение к старшим
7. Подражание Западу
8. Стремление создать семью
9. Рок-музыка
10. Карьера
11. Секс
12. Интеллект
После проведения его были выделены 3 основных фактора (см. табл. 5.8).
Таблица 5.8
Дата добавления: 2015-09-11; просмотров: 990;
