Обработка информации
Полученную в ходе сбора социологическую информацию следует упорядочить и формализовать, т. е. выразить языком цифр, коэффициентов. Группировка, подсчет описательных характеристик, коэффициентов корреляции – простейшие математико–статистические методы обработки информации. Для обработки небольших массивов информации (от нескольких десятков до 100 анкет) можно использовать ручной метод (для этого нужно четко знать процесс расчета всех показателей). При больших объемах выборки и при проведении cложных статистических анализов социологической информации обработка ведется на ЭВМ с использованием специальных программ.
Мощным средством текстового анализа является программный продукт “WINMAXpro”, который дает возможность комбинировать процедуры качественного и количественного анализа. При помощи его можно проводить анализ стенограмм качественных интервью, полевых заметок, писем и документов, ответов на открытые вопросы, протоколов наблюдений, экспертных интервью. Он позволяет интерпретировать, систематизировать, совершенствовать, объяснять отдельные абзацы текста, искать характерное содержимое текста, а также сравнивать различные тексты, стандартизировать их или объединять общее различных текстов в новый текст. Принцип работы этого пакета основан на разбивке текста на отдельные сегменты и последующем присваивании им определенных кодов.
Один из самых распространенных пакетов обработки статистической информации – пакет SPSS/PC+, разработанный в США. Данные можно вводить непосредственно с помощью этого пакета или использовать специальную программу DATA ENTRY, которая частично контролирует ввод информации в ЭВМ, что позволяет избежать многих ошибок, например, таких, как выход за диапазон вариантов ответов. Пакет SPSS удобен и прост в работе. Для работы с ним можно использовать “меню” или при помощи специального программного языка писать программы обработки. Этот программный продукт обладает большим набором возможностей. Помимо проведения простейшей обработки социологической информации он позволяет проводить такие сложные методы анализа, как регрессионный, дисперсионный, факторный, кластерный. На выходе получаются легко читаемые информативные таблицы, которые при необходимости можно представить в графическом виде.
Перед вводом данных в машину все варианты ответов должны быть закодированы, ответы на открытые вопросы выписаны, при необходимости сгруппированы и также закодированы.
Для кодирования открытых вопросов составляется кодификатор, с помощью которого полученные от респондентов ответы объединяются в некие смысловые категории и им присваиваются символы (числа). Кодификатор представляет из себя перечень всех (либо сгруппированных по какому-либо основанию) ответов респондентов, каждому из которых присваивается соответствующий номер. При кодировании открытых вопросов необходимо, чтобы категории были исчерпывающими; одинаковые ответы должны входить в одну категорию; в соответствии с постановкой вопроса должна соблюдаться качественная однородность выделенных категорий.
Перед началом обработки собранной социологической информации в соответствии с целями, задачами и гипотезами исследования составляется логическая программа этой обработки.
Логическая программа – это задание, которое дает социолог программисту. Программа определяет направление, диапазон и глубину анализа первичных данных. В компетенцию социолога входит то, как будет обсчитываться массив, каким видам анализа должна быть подвергнута полученная информация. И именно в логической программе отражается весь набор и последовательность необходимых операций. Наиболее часто в практике социологических исследований встречаются следующие задачи: расчет по одному, двум и более признакам, объединение нескольких признаков в целях выделения типологических групп и др.
Пример логической программы.
1. Рассчитать линейное распределение ответов на вопросы анкеты по всему массиву.
2. Сформировать массивы по следующим признакам: пол, возраст, социальное положение. Внутри каждого массива рассчитать линейное распределение ответов на вопросы анкеты.
3. Построить таблицы сопряженности следующих признаков:
- 2х15; 5х15,21
- Рассчитать коэффициенты парной корреляции.
4. Осуществить факторный анализ по признакам 3–10.
Первым шагом обработки является подсчет частот появления каждого варианта признака (линейного распределения ответов на вопросы анкеты) и упорядочивание полученных данных в таблице одномерного распределения. Для подсчета частот вручную применяется метод графической записи, при котором каждый десяток изображается в виде прямоугольника с диагоналями. Сначала отмечаются вершины прямоугольника, потом стороны, потом диагонали. Соответствие между числами и фрагментами изображения следующее:

Подсчитанные частоты переводятся в процентное отношение. Выражение частот в процентном отношении дает возможность определить меру оценки или отношения респондентов к явлению или процессу, обозначенному признаком, лежащим в основе того или иного вопроса анкеты. Кроме того, это позволяет сравнивать вариационные ряды с различным числом наблюдений. Формула выражения частот в процентном отношении:
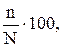 (5.1)
(5.1)
где N – общее число респондентов (объем выборки), n – число респондентов из состава данной группы, характеризующихся сходным отношением к предмету исследования.
Варианты ответов на вопросы, которые заданы в номинальных шкалах, желательно упорядочить в возрастающем или убывающем порядке, т. е. ранжировать их по частотам (например, рейтинги лидеров партий, рейтинги партий и т. д.). Другие шкалы упорядочиваются по значениям признака (вариантам ответов), что дает возможность визуально определить его минимальное и максимальное значение, оценить среднее значение (например, определить минимальное, максимальное число членов семьи, значение среднего числа членов семьи).
В некоторых случаях, когда число вариантов признака достаточно велико или значения признака вообще могут не повторяться, строятся интервальные ряды. Интервал указывает определенные пределы значений варьирующегося признака и обозначается нижней и верхней границами интервала. Например, если в анкете возраст указывался точным числом, полученная таблица линейного распределения станет очень объемной. Поэтому возрастную шкалу следует разбить на интервалы.
Приведем пример (см.5.1).
Таблица 5.1
Линейное распределение вариантов ответов на вопрос “Нравится ли Вам специальность, по которой Вы учитесь?”
| Варианты ответов | Коды ответов | Частота | Процент от всего массива | Действи-тельный процент | Накопленный процент | ||||
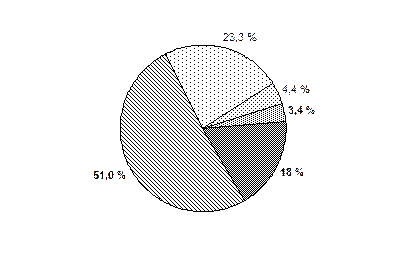
| Нравится | 51,0 | 62,1 | 62,1 | ||||||
| Скорее нравится | 23,3 | 28,4 | 90,5 | ||||||
| Скорее не нравится | 4,4 | 5,4 | 95,9 | ||||||
| Не нравится | 3,4 | 4,1 | 100,0 | ||||||
| Трудно сказать | 18,0 | - | |||||||
| Всего | 100,0 | 100,0 |
При обработке исходной социологической информации нужно обратить внимание на тот факт, что иногда респонденты отказываются отвечать на поставленные вопросы или затрудняются дать ответ. Это нужно учитывать при дальнейшей обработке: при расчете средних величин, вариации, корреляции признаков анкеты, при проведении более сложного анализа (факторного, кластерного и т. д.). Пятая колонка таблицы – это проценты, вычисленные от числа респондентов, давших определенный ответ на вопрос анкеты. Шестая колонка таблицы – накопленный процент.
Чтобы сделать более наглядным распределение значений признаков и взаимосвязь между ними, удобно прибегать к графическому представлению социологической информации. Наиболее распространенными видами графического изображения являются полигон распределения, который применяется для изображения дискретных рядов распределения; гистограмма распределения – для изображения интервальных рядов; различные виды диаграмм (сравнительные, структурные, диаграммы динамики) [81, 103-130].
Пример структурной диаграммы (по данным табл. 5.1):
|
Для анализа и сравнительной характеристики различных распределений применяются обобщающие показатели вариационного ряда. В качестве показателей центра распределения (среднего значения признака) используются средняя арифметическая (взвешенная), мода и медиана. Средняя арифметическая взвешенная вычисляется по формуле:
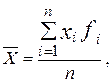 (5.2)
(5.2)
где xi – значения вариантов, fi – частота их появления, n – объем выборки.
Средняя величина рассчитывается не только для количественных признаков (средний возраст, средняя заработная плата и т. д.), но и для качественных признаков, выраженных в порядковых шкалах, путем приписывания им количественных индексов.
Индекс удовлетворенности или значимости рассчитывается по формуле:
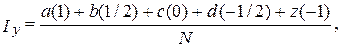 (5.3)
(5.3)
где Iу – индекс удовлетворенности, a, b, c, d, z – количество респондентов, избравших данный ответ, причем с – число респондентов, затруднившихся ответить, N – общее число респондентов. 1, 1/2, 0, -1/2, -1 – баллы, присвоенные вариантам ответов на вопрос (1 – положительный ответ, -1 – отрицательный). Если индекс равен +1, можно говорить о полной удовлетворенности,
-1 – полной неудовлетворенности.
Рассчитаем индекс значимости на примере данных, представленных в таблице 5.1.
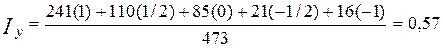 .
.
Индекс значимости довольно высокий. Можно судить о том, что удовлетворенность выбранной специальностью довольно высокая.
Оценка удовлетворенности может быть вычислена в баллах. В этом случае каждому из вариантов ответов приписывается определенный вес. Положительному ответу приписывается высший балл, отрицательному – низший. Затем исчисляется средняя арифметическая взвешенная.
В том случае, если альтернативный тип вопроса состоит из трех делений с равными интервалами, можно рассчитать индекс контрастности. Исчисление индекса осуществляется по формуле:
 (5.4)
(5.4)
где Iк – индекс контрастности, a, b – веса полярных ответов в процентах, 100 – постоянная величина, применяемая для удобства расчета.
Например, ответы на вопрос “Устраивают ли Вас взаимоотношения в Вашем коллективе?” распределились следующим образом:
Устраивают 80,7 %
Не устраивают 6,4 %
Трудно сказать 12,9 %
.
Индекс контрастности в этом случае будет равен:
 .
.
Поскольку значение индекса изменяется в пределах от –1 (полная неудовлетворенность) до +1 (полная удовлетворенность), можно сказать, что удовлетворенность взаимоотношениями очень высокая.
Индексы и баллы лучше всего использовать в сравнении.
Медиана делит вариационный ряд на две части, равные по числу вариантов. Если число нечетно, медиана соответствует варианту, стоящему в середине ранжированного ряда (N=n+1/2). При четном числе вариантов медиана – среднее между вариантами, стоящими на n/2 и (n+2)/2 месте. Например, для ряда 1,3,4,5,8 медиана равна 4, а для ряда 1,3,4,5,7,8 медиана равна 4,5. Мода – это наиболее часто встречающееся значение признака.
Средняя величина дает обобщающую характеристику всей совокупности изучаемого признака. Однако колеблемость, изменяемость, вариация величин самого признака в разных рядах распределения при равных средних взвешенных может значительно различаться. Например, средний балл успеваемости в параллельных классах может быть равным, хотя при этом в одном классе может быть много отличников и двоечников, а в другом – успеваемость учащихся сравнительно равномерная.
Для измерения вариации признака используются различные абсолютные и относительные показатели. К абсолютным показателям относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение.
Размах вариации R представляет собой разность между минимальным и максимальным значениями признака.
R=xmax – x min . (5.5)
Среднее линейное отклонение вычисляется по формуле:
 . (5.6)
. (5.6)
Дисперсия s2 – средняя из квадратов отклонения вариантов значения признака от их средней величины.
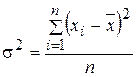 . (5.7)
. (5.7)
Среднее квадратичное отклонение есть корень квадратный их дисперсии:
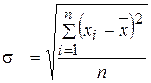 . (5.8)
. (5.8)
Чем больше дисперсия (соответственно среднее квадратичное отклонение), тем больше рассеивание значений признака вокруг своего среднего. Дисперсия и среднеквадратичное отклонение входят в большинство теорем теории вероятностей, служащих фундаментом математической статистики. Дисперсия может быть разложена на составные элементы, которые позволяют оценить влияние различных факторов на вариацию признака.
Приведем пример расчета абсолютных показателей. При опросе 30 школьников, употребляющих спиртные напитки, получено следующее распределение ответов:
| Сколько Вам было лет, когда Вы впервые попробовали спиртные напитки? | Частота | % | ||
| 10 лет | 10,0 | |||
| 11 лет | 6,7 | |||
| 12 лет | 23,3 | |||
| 13 лет | 30,0 | |||
| 14 лет | 23,3 | |||
| 15 лет | 6,7 | |||
| Всего | 100,0 |
Вариационный размах R=15–10=5 показывает, в каких пределах колеблются ответы опрошенных школьников. В среднем школьники впервые попробовали спиртные напитки около 13 лет (средняя взвешенная равна 12,7). Этот возраст также встречается чаще всего в ответах (мода равна 13). Вычислим дисперсию:
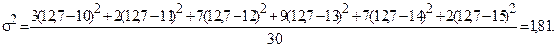 Среднеквадратичное отклонение s равно 1,35.
Среднеквадратичное отклонение s равно 1,35.
 Наиболее часто применяемый показатель относительной колеблемости признака – коэффициент вариации CV=σ/ . Он служит для сравнения величин рассеивания вокруг средней двух вариационных рядов. Большее рассеивание имеет тот из рядов, у которого коэффициент вариации больше. Коэффициент вариации используется также для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %.
Наиболее часто применяемый показатель относительной колеблемости признака – коэффициент вариации CV=σ/ . Он служит для сравнения величин рассеивания вокруг средней двух вариационных рядов. Большее рассеивание имеет тот из рядов, у которого коэффициент вариации больше. Коэффициент вариации используется также для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %.
Для нашего примера:
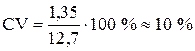
Вариация одного признака находится в тесной связи и взаимодействии с вариацией других признаков. При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков – результативных. Зависимость между признаками может быть функциональной и статистической. При функциональной зависимости изменение одного признака ведет к немедленному изменению значения другого. Статистическая зависимость – это зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В таком случае статистическую зависимость называют корреляционной.
Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов. Значения факторного признака располагают в возрастающем порядке и затем прослеживают изменение величины результирующего признака. Однако при наличии большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, анализ таких рядов довольно затруднителен. Поэтому чаще всего социологические данные представляются в виде двухмерных таблиц сопряженности (корреляционных таблиц).
Поясним устройство таблицы сопряженности.
В первой строке таблицы указываются наблюдаемые значения первого признака, а в первом столбце – наблюдаемые значения второго признака. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений. В последнем столбце записываются суммы частот строк, а в последней строке – суммы частот столбцов (эти частоты называются маргинальными частотами), в нижнем правом углу – сумма всех частот. Одновременно с абсолютными частотами записывается и процентное отношение. Процентное отношение вычисляется по вертикали и по горизонтали. Данные на пересечении строк и столбцов дают нам информацию о взаимосвязи двух признаков.
Таблица 5.2
| Чувствуете ли Вы себя в безопасности на улицах города? | Пол | В целом по массиву | ||||
| Мужской | Женский | |||||
| Да, чувствую себя в безопасности | 37,5 5,9 | 5 62,5 10,2 | 8 100,0 8,0 | |||
| Скорее да, чем нет | 84,2 31,4 | 3 15,8 6,1 | 19 100,0 19,0 | |||
| Трудно сказать | 54,5 11,8 | 5 45,5 10,2 | 11 100,0 11,0 | |||
| Скорее нет, чем да | 45,0 17,6 | 11 55,0 22,4 | 20 100,0 20,0 | |||
| Нет, не чувствую себя в безопасности | 40,5 33,3 | 25 59,5 51,0 | 42 100,0 42,0 | |||
| В целом по массиву | 51,0 | 49 49,0 | 100 100,0 |
При просмотре такой таблицы, если читать по горизонтали, видно, что среди тех, кто чувствует себя в полной безопасности на улицах города, 37,5 % мужчин и 62,5 % женщин, среди тех, кто ответил “скорее да, чем нет”, 84,2 % мужчин и 15,8 % женщин и т. д. Для оценки того, как себя чувствуют на улицах города только мужчины или только женщины, таблицу следует читать по вертикали.
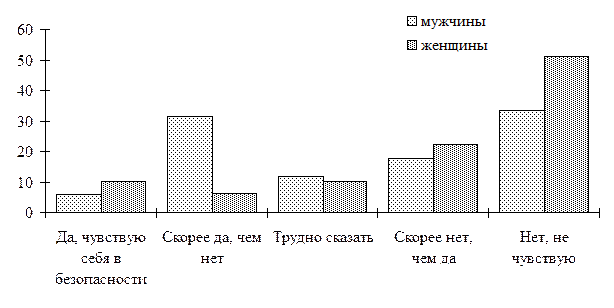
Графическое представление корреляционной таблицы.
Статистический показатель, используемый для проверки гипотезы о том, что признаки в столбце и строке таблицы независимы, – критерий согласия Пирсона l2 “хи-квадрат”.
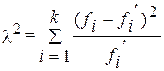 . (5.9)
. (5.9)
где fi – эмпирические частоты (т. е. частоты вариантов ответов на вопрос анкеты),
fi’ – ожидаемые (теоретические) частоты (теоретическая частота в ячейке таблицы равна произведению маргинальных частот – сумм частот по строке и столбцу– деленному на общее число наблюдений). Рассчитаем теоретические частоты для нашего примера.
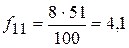

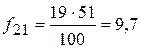
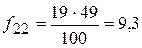
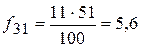
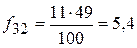
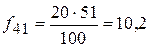
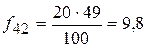
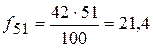
 .
.
Так как значение l2 зависит от числа строк и столбцов таблицы, необходимо определить число степеней свободы таблицы. Число степеней свободы – это число ячеек таблицы, которое можно заполнить произвольно при фиксированных маргинальных значениях: df= (r–1) (c–1). В нашем примере число строк (r) равно 5, а число столбцов (с) равно 2. Следовательно, число степеней свободы
df=(r–1)(c–1)=4. По таблицам математической статистики устанавливается вероятность появления рассчитанного значения, соответствующего данному числу степеней свободы в предположении независимости признаков, либо табличное значение критерия, соответствующего уровню значимости 0,05 или 0,01. Если l2расч<l2табл, то гипотеза о независимости признаков не опровергается.
Таблица 5.3
Дата добавления: 2015-09-11; просмотров: 1079;
