Расчет критерия согласия Пирсона
| fi | f'i | fi – f'i | (fi – f'i)2 | (fi – f'i)2/ fi | ||||
| 4,1 | –1,1 | 1,21 | 0,30 | |||||
| 3,9 | 1,1 | 1,21 | 0,31 | |||||
| 9,7 | 6,3 | 39,69 | 4,09 | |||||
| 9,3 | –6,3 | 39,69 | 4,27 | |||||
| 5,6 | 0,4 | 0,16 | 0,03 | |||||
| 5,4 | –0,4 | 0,16 | 0,03 | |||||
| 10,2 | –1,2 | 1,44 | 0,14 | |||||
| 9,8 | 1,2 | 1,44 | 0,15 | |||||
| 21,4 | –4,4 | 19,36 | 0,90 | |||||
| 20,6 | 4,4 | 19,36 | 0,94 | |||||
| å=11,16 |
l2=11,16.
При числе степеней свободы 4 и уровне значимости 0,05 находим табличное значение l2табл =9,5. Так как l2расч>l2табл, гипотеза о независимости признаков в строке и столбце таблицы отвергается.
Критерий “хи-квадрат” вычисляется для подтверждения гипотезы о независимости признаков, но он не характеризует тесноту связи. Для определения тесноты связи можно использовать коэффициенты сопряженности Пирсона и Крамера. Они рассчитываются для таблиц размером схk, если признаки измерены в шкале наименований.
1. Коэффициент сопряженности Пирсона
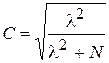 . (5.10)
. (5.10)
Коэффициент может принимать значения только от 0 до 1 (0 – отсутствие сопряженности, 1 – полная сопряженность). Однако этот коэффициент не может принимать значения, равные 1, максимальное возможное значение зависит от числа строк и столбцов. Например, для таблиц 4х4 максимальное значение коэффициента 0,87.
Для нашего примера
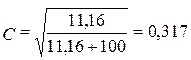 .
.
2. Коэффициент сопряженности Крамера
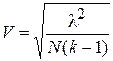 , (5.11)
, (5.11)
где k – минимальное число из числа строк и столбцов.
Для нашего примера
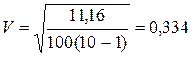 .
.
Оценка значимости полученных коэффициентов производится по критерию l2.
Для случая дихотомических (таблицы 2х2) признаков (например, пола, партийного положения, семейного положения, шкалы “да – нет”) мера связи между двумя признаками оценивается с помощью коэффициента ассоциации Пирсона.
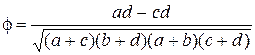 , (5.12)
, (5.12)
где а, b, c, d – эмпирические частоты в ячейках таблицы.
Рассчитаем этот коэффициент на примере корреляционной табл. 5.4.
Таблица 5.4
| Достаточно ли представлены, на Ваш взгляд, женщины Вашего населенного пункта в органах власти и управления? | Пол | В целом по массиву | |
| Мужской | Женский | ||
| Да | a | b | 13 (a+b) |
| Нет | c | d | 48 (c+d) |
| В целом по массиву | (a+c) | (b+d) |
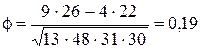
Значимость полученного коэффициента также производится по критерию l2.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют коэффициенты ранговой корреляции Спирмена и Кендала. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, что их значения можно упорядочить или проранжировать по степени убывания или возрастания признака. Ранг – это порядковый номер значений признака, расположенных в порядке убывания или возрастания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называют связными. Коэффициент ранговой корреляции Спирмена в случае несвязных рангов вычисляется по формуле:
 , (5,13)
, (5,13)
где di – разности рангов, l – число пар рангов. Коэффициент изменяется от –1 до +1. При l > 30 значимость коэффициента проверяется на основе t-критерия Стьюдента. Расчетное значение критерия:
 . (5.14)
. (5.14)
Значение коэффициента считается значимым, если tрасч>tкр.
При l £ 30 значимость коэффициента при заданном уровне значимости и определенном объеме выборочных данных проверяется по таблице.
Вычисления коэффициента Спирмена для связных рангов более громоздки. Поэтому на практике для связных и несвязных рангов удобнее использовать формулу для несвязных рангов. Вычисление коэффициента приведено в табл. 5.5:
Таблица 5.5
Сравнение основных жизненных ценностей студентов
в 1987 и 1991 гг.
| Жизненные ценности | Ранг | Ранг | ||||||
| 1. Иметь верных друзей | 91,1 | 81,5 | ||||||
| 2. Любовь | 68,7 | 55,6 | ||||||
| 3. Интересная профессия | 71,0 | 41,1 | ||||||
| 4. Учеба | 38,9 | 9,6 | ||||||
| 5. Уважение к старшим | 39,0 | 5,7 | ||||||
| 6. Сила | 20,7 | 30,9 | ||||||
| 7. Деньги | 27,0 | 43,6 | ||||||
| 8. Интеллект | 35,8 | 17,5 | 6,5 | |||||
| 9. Творчество | 20,2 | 4,8 | ||||||
| 10. Стремление создать семью | 41,2 | 14,3 | ||||||
| 11. Мода | 30,2 | 13,6 | ||||||
| 12. Музыка | 16,0 | 16,0 | ||||||
| 13. “Фирменные” вещи | 14,2 | 17,5 | 6,5 | |||||
| 14. Карьера | 11,0 | 16,5 | ||||||
| 15. Секс | 5,4 | 14,0 |
В нашем примере 8-я и 13-я позиции делят между собой шестое и седьмое места. Поэтому им соответственно приписываем ранг (6+7)/2, т. е. 6,5.
Используя данные, построим рабочую таблицу.
Таблица 5.6
Расчет коэффициента ранговой корреляции Спирмена.
| Номер признака | Ранг | Разность пар рангов | Квадрат разности рангов | |||||
| переменной | I | II | di | di2 | ||||
| –2 | ||||||||
| –8 | ||||||||
| –10 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| –5 | ||||||||
| –7 | ||||||||
| –5 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| å=383,5 |
Подставляем данные в формулу:
 .
.
Из таблицы критических значений Спирмена находим, что при l=15 и уровне значимости 0,05 rs должен быть не ниже 0,517. В нашем случае он равен 0,315, следовательно, между жизненными ценностями молодежи в 1987 и 1991 гг. нет значимой связи.
Для установления связи между количественными признаками (например, возрастом, зарплатой, количеством членов семьи) используется линейный коэффициент корреляции Пирсона (определение формы связи признаков можно осуществить путем построения графика взаимного изменения в декартовой системе координат).
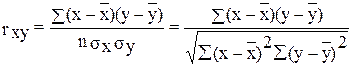 , (5.15)
, (5.15)
где x – факторный признак, y – результативный признак.
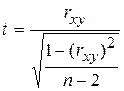 . (5.16)
. (5.16)
Для оценки существенности коэффициента корреляции используется критерий t (при n<50).
Полученное значение критерия сравнивается при заданном числе степеней свободы (df=n–2) и уровне значимости с табличным значением (табл. распределения Стьюдента). Если вычисленное значение критерия больше табличного, гипотеза о независимости признаков отвергается.
Проверку гипотезы об отсутствии связи можно сделать и без вычислений, пользуясь таблицей, составленной Р. Фишером. В этой таблице показывается величина коэффициента корреляции, которая может считаться существенной при данном количестве наблюдений. При пользовании таблицей величину коэффициента корреляции следует искать для числа степеней свободы, равного n–2. Чтобы считаться существенным при заданном уровне значимости, он должен быть не ниже табличного значения.
Линейный коэффициент корреляции может принимать любые значения в пределах от –1 до +1. Чем ближе коэффициент к 1 по абсолютной величине, тем теснее связь между признаками. Знак при коэффициенте линейной корреляции указывает на направление связи: при прямой зависимости коэффициент положительный, при противоположной – отрицательный, 0 – отсутствие линейной зависимости между признаками.
Предположим, что задача исследования состоит в определении степени зависимости уровня успеваемости студентов от уровня их удовлетворенности избранной специальностью. В качестве исходных данных взяты (в баллах) уровень успеваемости по студенческим группам и уровень удовлетворенности выбранной специальностью.
Таблица 5.7
Дата добавления: 2015-09-11; просмотров: 2033;
