Алгоритм теплового расчета

Использование при тепловых расчетах тяговых двигателей эквивалентных тепловых схем замещения с большим числом элементов приводит к необходимости решения систем дифференциальных или алгебраических уравнений большой размерности. Решение таких систем возможно только с применением численных методов.

Для решения системы дифференциальных уравнений используется метод Рунге-Кутта 4-го порядка. В методе Рунге-Кутта

решение получается в виде дискретного набора превышений температуры отдельных элементов электрической машины через некоторые промежутки времени, называемые шагом h. Шаг изменения времени может быть переменным или постоянным. Так как процесс изменения превышения температуры от времени в электрической машине описывается гладкой кривой, целесообразно использовать постоянный шаг, т.е. определить превышение температуры через одинаковые промежутки времени.

Для получения единственного решения метод Рунге-Кутта требует задания начальных условий. При тепловом расчете электрической машины в качестве начальных условий должны быть заданы превышения температуры в узлах тепловой схемы замещения, которые перед началом расчета могут быть положены равными нулю.

Согласно методу Рунге-Кутта превышение температуры в последующий момент времени определяется по формуле:

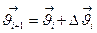
где 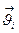- превышение температура в данный момент времени;

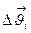- поправка к превышению температуры.

Стрелка над превышением температуры означает множество значений, равное числу уравнений системы.

Поправка 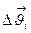вычисляется по формуле

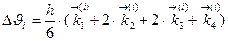
где 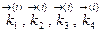- правые части системы дифференциальных уравнений вида (6.2), вычисляемые в 4-х различных точках на каждом шаге решения;

i – номер шага решения.

Вычисление 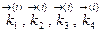производиться по следующим формулам

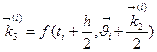
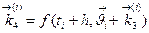
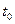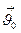На первом шаге решения индекс i принимает нулевое значение, т.е. используется начальные значения и . Вычисления проводятся для каждого дифференциального уравнения и на каждом шаге решения в заданном диапазоне изменения времени. Учет изменения коэффициента теплопроводности от температуры можно производить на каждом шаге решения или через определенное количество шагов.

Погрешность метода Рунге-Кутта зависит от величины шага h и ее оценка аналитически затруднительна. Поэтому на практике получают решения с шагом h, 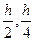и т.д. и на основании их анализа выбирают величину шага.

Для решения системы линейных алгебраических уравнений используется метод Гаусса. Прямоугольная матрица коэффициентов в этом методе при прямом ходе преобразуется в две треугольные, верхнюю – не нулевую и нижнюю, состоящую из нулей. При обратном ходе верхняя треугольная матрица используется для получения решения.

Блок-схема программы теплового расчета представлена на рис.4.

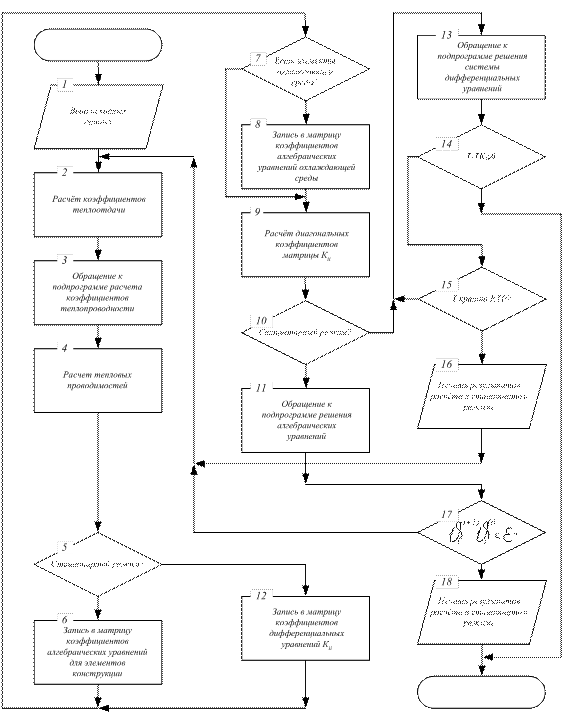
Рис.4. Блок-схема программы теплового расчёта