Математическое описание тепловой схемы замещения

Для получения математической модели в методе эквивалентных схем замещения используется уравнение теплового баланса (закон сохранения энергии).

Для однородного тела уравнение теплового баланса записывается следующим образом:

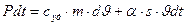
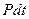- потери, выделяемые в элементе за время ;

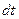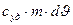- идёт на нагревание элемента;

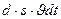-передаётся охлаждающему воздуху;

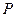-потери в элементе;

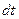-промежуток времени;

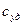-удельная теплоёмкость элемента;

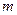-масса элемента;

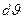-превышение температуры элемента;

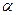-коэффициент теплоотдачи с обдуваемой поверхности;

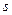- площадь обдуваемой поверхности;

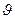-температура превышение температуры.

Так как элементы схемы замещения связаны между собой, то уравнение теплового баланса для i – го элемента имеет вид:

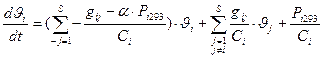, (3)

где S – общее число элементов, на которое разбита электрическая машина, включая и элементы охлаждающего воздуха;

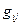- тепловая проводимость между i-м и j-м элементами;

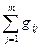- сумма тепловых проводимостей между i-м элементом конструкции и всеми остальными элементами, имеющими с ним тепловую связь;

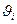- превышение температуры рассматриваемого элемента;

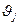- превышение температуры элементов, имеющих связи с рассматриваемым элементом;

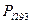- потери в i-м элементе при температуре 293К;

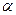- температурный коэффициент сопротивления (для меди );

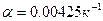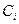- теплоемкость i-го элемента.

Теплоемкость элемента вычисляется по формуле:

,

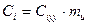где 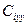- удельная теплоемкость i-го элемента;

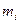- масса i-го элемента.

Обычно, при разбиении электрической машины на элементы, изоляцию не выделяют отдельным элементом, а объединяют ее с элементом меди обмотки. В этом случаи эквивалентная теплоемкость элемента вычисляется по формуле:

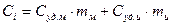
где 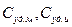- соответственно, удельные теплоемкости меди и изоляции;

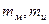- соответственно, масса меди и изоляции i-го элемента.

При расчете нестационарных тепловых процессов в электрической машине необходимо решать систему обыкновенных дифференциальных уравнений вида (3).

Для стационарного теплового процесса уравнение (3) принимает вид:

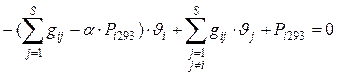(4)

Уравнение вида (3) является обыкновенным дифференциальным уравнением с постоянными коэффициентами, вида (4) линейным алгебраическим уравнением.

При решении систем уравнений вида (3) или (4) необходимо учитывать подогрев охлаждающего воздуха. Охлаждающий воздух, так же как и элементы конструкции, разбивается на элементы, которые вводятся в схему замещения.

Уравнение связи элемента воздуха с элементами конструкции получается из уравнения теплового баланса.

Для i-гo элемента охлаждающего воздуха можно записать:

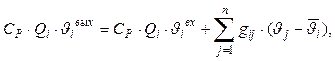(5)

где 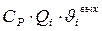- количество тепла, уносимого воздушным потоком из i-гo элемента;

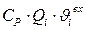- количество тепла, поступившего с воздухом из предыдущего (i-l)-гo элемента;

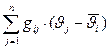- количество тепла, полученное от элементов в конструкции;

n - количество элементов конструкции;

С_Р - удельная теплоемкость охлаждающей среды;

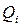- расход воздуха через i-й элемент охлаждающей среды;

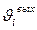- превышение температуры на выходе i-гo элемента;

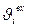- превышение температуры на входе i-гo элемента;

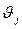- превышение температуры элементов конструкции, имеющих связь с i-м элементом охлаждающего воздуха;

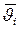- среднее превышение температуры охлаждающего воздуха:

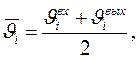(6)

На основании (5) и (6) можно записать:

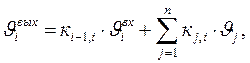(7)

к_i-1,i - коэффициент связи между i и (i-l)-м элементами охлаждающей среды,

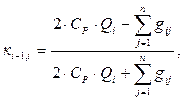
к_i,j - коэффициент связи между j-м элементом конструкции и i-м элементом охлаждающей среды

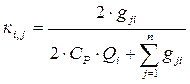
Уравнение (7) является линейным алгебраическим уравнением.

На основании (3), (4) и (7) можно утверждать, что тепловая схема замещения в переходных режимах описывается системой обыкновенных дифференциальных уравнений для элементов конструкции и системой линейных алгебраических уравнений для элементов охлаждающего воздуха. В стационарных тепловых режимах тепловая схема замещения описывается системой линейных алгебраических уравнений для элементов конструкции и элементов охлаждающего воздуха.