Выборочные функции линейной и квадратичной регрессии

Случайные величины X и Y называются связанными линейной корреляцией, если обе функции регрессии для этих величин линейны, т.е.

и .

Получим с помощью метода наименьших квадратов в этом случае явный вид выборочных функции линейной регрессии. Для выборки объема 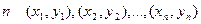величин X и Y сумма квадратов отклонений имеет вид 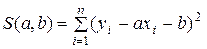. Отсюда, используя (1), получим систему из двух уравнений с двумя неизвестными

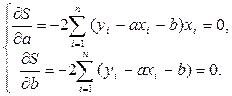
Преобразуем эту систему и получим систему 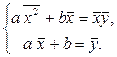Решим ее по правилу Крамера.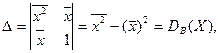 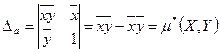. Поэтому 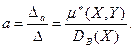Здесь число 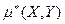называется выборочным корреляционным моментом для выборки величин X и Y.

Обозначим 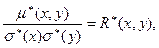где Здесь 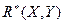называется выборочным коэффициентом корреляции величин X и Y. Тогда

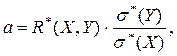
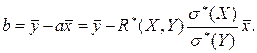
Окончательно получим, что выборочная функция линейной регрессии Y на X имеет вид

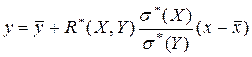(2)

Аналогично получается выборочная функция линейной регрессии X на Y

(3)

Если выборочная функция регрессии имеет вид (квадратичная регрессия), то , а неизвестные параметры 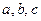определяются из системы уравнений:

Выводы. По данной теме нами были рассмотрены основные понятиякорреляционного анализа, виды зависимостей между случайными величинами, функции регрессии, Выборочные функции регрессии и их нахождение методом наименьших квадратов. В частности, рассматривались линейная и параболическая функции регрессии.