Математичний додаток
9.1 Вектори та математичні дії з векторами
Величини, для визначення яких достатньо знати лише їх числове значення, називаються скалярами.
Величини, що характеризуються числовим значенням і напрямком називаються векторами. Числове значення вектора називається його модулем (числовою величиною): 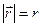 – модуль вектора.
– модуль вектора.
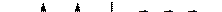 Вектори, які напрямлені уздовж паралельних прямих, називаються колінеарними. Колінеарні вектори можуть бути паралельними і антипаралельними.
Вектори, які напрямлені уздовж паралельних прямих, називаються колінеарними. Колінеарні вектори можуть бути паралельними і антипаралельними.
Вектори, які паралельні до однієї площини, називаються компланарними.
Однакові за модулем колінеарні вектори, напрямлені в один бік , вважаються рівними; рівні за модулем антипаралельні вектори вважаються такими, що мають різні знаки (див. рис. 55).
9.1.1 Елементарні дії з векторами
Вектори можна додавати та віднімати. При цьому пам’ятаємо, що паралельне перенесення вектора не змінює його (ні модуль, ні напрямок).
а). Додавання векторів.
Вектори можна додавати за правилом паралелограма. Сума двох векторів 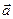 і
і 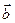 (рис. 56, а) є діагоналлю
(рис. 56, а) є діагоналлю 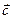 паралелограма, сторонами якого є вектори
паралелограма, сторонами якого є вектори 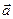 і
і 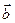 (рис. 56, б), при цьому початки векторів суміщають.
(рис. 56, б), при цьому початки векторів суміщають.
 |
Іншим способом додавання векторів є побудова, при якій вектор
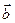 переносять паралельно самому собі таким чином, щоб його початок співпав із кінцем вектора
переносять паралельно самому собі таким чином, щоб його початок співпав із кінцем вектора 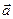 . При цьому сумарний вектор
. При цьому сумарний вектор 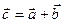 з’єднує початок вектора
з’єднує початок вектора 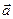 з кінцем перенесеного вектора
з кінцем перенесеного вектора 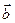 (рис. 56, в)Останній метод побудови сумарного вектора більш зручний у задачах, в яких потрібно знайти суму трьох і більше векторів (рис. 56, г).
(рис. 56, в)Останній метод побудови сумарного вектора більш зручний у задачах, в яких потрібно знайти суму трьох і більше векторів (рис. 56, г).
 б). Різниця векторів.
б). Різниця векторів.
Різницею двох векторів 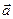 і
і 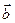 є вектор
є вектор 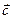 , який у сумі з вектором
, який у сумі з вектором 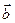 дає вектор
дає вектор 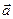 :
:
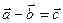 ,
, 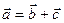 (9.1)
(9.1)
 |
в). Радіус-вектор.
Радіус-вектором точки називають вектор, який проведено з початку координат у дану точку. Радіус-вектор однозначно визначає положення точки у просторі.
г). Розкладання радіус-вектора на складові (рис. 58).
Кожен вектор 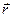 можна розкласти на складові, сума яких дає вектор
можна розкласти на складові, сума яких дає вектор 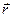 . На рисунку
. На рисунку 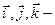 орти, вектори, довжина яких дорівнює 1=
орти, вектори, довжина яких дорівнює 1= 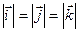 , а напрямки співпадають відповідно з осями
, а напрямки співпадають відповідно з осями 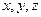 .
.

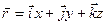
 (9.2)
(9.2)
д). Проекція вектора на вісь (рис. 59).
Розглянемо вектор 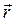 , що лежить у площині
, що лежить у площині 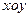 . Проекція вектора
. Проекція вектора 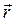 на вісь
на вісь 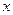 – відрізок між проекціями точок, що відповідають координатам початку і кінця вектора на вісь
– відрізок між проекціями точок, що відповідають координатам початку і кінця вектора на вісь 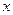 .
.
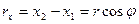 (9.3)
(9.3)
Подібно: 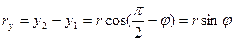
 е). Множення вектора на скаляр.
е). Множення вектора на скаляр.
У результаті множення вектора 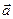 на скаляр
на скаляр 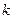 одержується вектор
одержується вектор 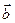 , модуль якого у
, модуль якого у 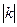 разів більший за модуль
разів більший за модуль 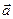 , а напрям визначається знаком
, а напрям визначається знаком 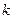 :
:
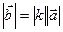 , тому
, тому 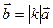 при
при 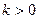 та
та 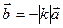 при
при 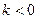 .
.
Ділення вектора на скаляр 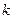 рівнозначне множенню цього вектора на
рівнозначне множенню цього вектора на 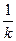 .
.
9.1.2 Скалярний добуток двох векторів
Скалярним добутком двох векторів 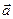 і
і 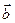 називається скаляр, чисельно рівний добутку модулів цих векторів на косинус кута
називається скаляр, чисельно рівний добутку модулів цих векторів на косинус кута 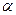 між ними (рис. 60).
між ними (рис. 60).
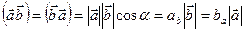 (9.4)
(9.4)
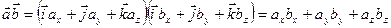 , (9.5)
, (9.5)
 |
оскільки
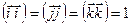 (
( 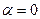 ), а
), а 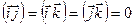 (
( 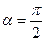 )
)
9.1.3 Векторний добуток двох векторів.
Векторним добутком двох векторів 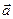 і
і 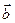 називається вектор
називається вектор 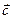 (див. рис. 61), який має наступні властивості:
(див. рис. 61), який має наступні властивості:
а) модуль вектора 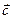 дорівнює добутку модулів векторів
дорівнює добутку модулів векторів 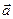 і
і 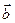 на синус кута між ними;
на синус кута між ними;
 б) вектор
б) вектор 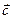 перпендикулярний до площини, у якій лежать вектори
перпендикулярний до площини, у якій лежать вектори 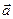 і
і 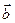 , причому його напрямок визначається правилом правого гвинта: якщо дивитися у напрямку
, причому його напрямок визначається правилом правого гвинта: якщо дивитися у напрямку 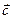 , то поворот, здійснений від першого множника до другого , повинен здійснюватись по найкоротшому шляху за ходом годинникової стрілки.
, то поворот, здійснений від першого множника до другого , повинен здійснюватись по найкоротшому шляху за ходом годинникової стрілки.
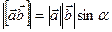 (9.6)
(9.6)
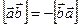 (9.7)
(9.7)
Простою геометричною інтерпретацією векторного добутку є наступне (див. рис. 62): векторний добуток двох векторів чисельно дорівнює площі паралелограма, побудованого на векторах 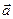 і
і 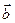 :
:
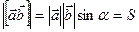 (9.8)
(9.8)
Вираз для векторного запису векторного добутку двох векторів у проекціях на осі 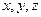 має наступний вигляд:
має наступний вигляд:
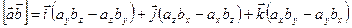 (9.9)
(9.9)
 |
Вираз (9.9) отримується шляхом розрахунку наступного визначника:
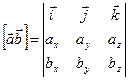
9.1.4 Подвійний векторний добуток трьох векторів
Він дається виразом:
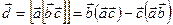 . (9.10)
. (9.10)
Геометрично вектор 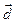 перпендикулярний до площини, в якій лежать вектори
перпендикулярний до площини, в якій лежать вектори 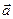 та
та 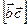 .
.
9.2 Поняття функції багатьох змінних. Частинні похідні. Повний диференціал. Градієнт скалярної функції багатьох змінних
В багатьох задачах фізики маємо справу із змінними величинами, значення яких повністю визначаються певним набором інших змінних величин. Наприклад, швидкість матеріальної точки при її русі під дією сили залежить від координат і часу: 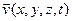 , а при розгляді нестаціонарного руху рідини швидкість частинок рідини також була функцією координати
, а при розгляді нестаціонарного руху рідини швидкість частинок рідини також була функцією координати 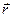 і часу
і часу 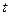 . Подібні функціональні залежності, в яких деяка змінна величина є функцією певної кількості незалежних змінних величин, називають функціями багатьох змінних.
. Подібні функціональні залежності, в яких деяка змінна величина є функцією певної кількості незалежних змінних величин, називають функціями багатьох змінних.
Розглянемо функцію 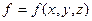 , визначену в деякому околі точки
, визначену в деякому околі точки 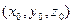 . Зафіксуємо змінні
. Зафіксуємо змінні 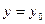 та
та 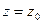 . В результаті отримаємо функцію
. В результаті отримаємо функцію 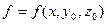 , залежну від однієї змінної. Якщо ця функція має похідну за змінною
, залежну від однієї змінної. Якщо ця функція має похідну за змінною 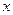 , то цю похідну назвемо частинною похідною функції
, то цю похідну назвемо частинною похідною функції 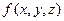 :
:
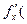
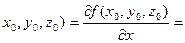
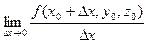
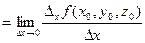 .
.
Величину 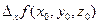 називають частинним приростом функції
називають частинним приростом функції 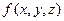 за зміною
за зміною 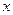 у точці
у точці 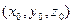 . Подібно можна знайти
. Подібно можна знайти 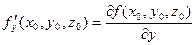 та
та 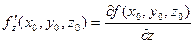 . Отриманий результат справедливий не лише для точки
. Отриманий результат справедливий не лише для точки 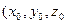 ), але і для довільної точки
), але і для довільної точки 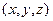 . Пам’ятаємо лише, що частинну похідну беруть згідно з правилами диференціювання функції однієї змінної.
. Пам’ятаємо лише, що частинну похідну беруть згідно з правилами диференціювання функції однієї змінної.
Приріст функції 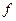 , обумовлений змінами
, обумовлений змінами 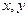 та
та 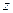 на
на 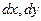 та
та 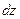 може бути записаний у вигляді
може бути записаний у вигляді
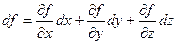 (9.11)
(9.11)
Вираз (9.11) є повним диференціалом функції 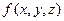 . Відзначимо, що повний диференціал може мати лише диференційована функція в точці
. Відзначимо, що повний диференціал може мати лише диференційована функція в точці 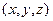 . Вираз (9.11) дає лінійні стосовно
. Вираз (9.11) дає лінійні стосовно 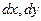 та
та 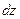 прирости функції
прирости функції 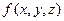 .
.
Якщо сукупність змінних 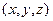 вважати складовими деякого вектора
вважати складовими деякого вектора 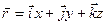 , то у тривимірному просторі повний диференціал
, то у тривимірному просторі повний диференціал 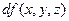 можна виразити як скалярний добуток вектора
можна виразити як скалярний добуток вектора 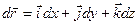 на вектор
на вектор 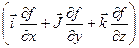 :
:
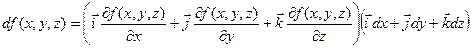 (9.12)
(9.12)
Таким чином
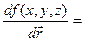
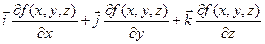 =
= 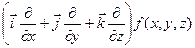 ,
,
або: 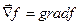 (9.13)
(9.13)
Тут диференціальний оператор Набла:
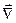 =
= 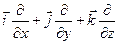 . (9.14)
. (9.14)
Вираз (9. 13) показує операцію знаходження градієнта 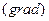 функції
функції 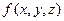 .Напрямок вектора
.Напрямок вектора 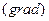
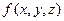 дає напрямок найшвидшої зміни функції
дає напрямок найшвидшої зміни функції 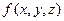 .
. 
9.3 Комплексні числа та їх використання при розгляді коливних і хвильових процесів
Положення точки на площині задаємо комплексним числом
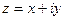 (9.15)
(9.15)
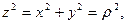
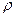 – модуль комплексного числа,
– модуль комплексного числа,
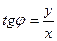
 Якщо використати формулу Ейлера
Якщо використати формулу Ейлера
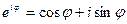 , (9. 16)
, (9. 16)
то
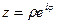
Нехай 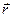 – радіус-вектор матеріальної точки, що обертається по колу з кутовою швидкістю
– радіус-вектор матеріальної точки, що обертається по колу з кутовою швидкістю 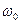 , тоді
, тоді
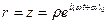 ,
,
де 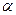 початкова фаза руху.
початкова фаза руху.
Якщо взяти дійсну частину виразу, отримаємо рівняння гармонійних коливань по осі 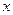 :
:
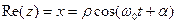 (9. 17)
(9. 17)
Для опису коливань по осі 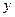 шукаємо уявну частину виразу
шукаємо уявну частину виразу
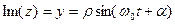 (9. 18)
(9. 18)
Вирази типу (9.17) зручно використовувати для опису коливних та хвильових процесів. Зокрема, вираз:
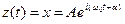 (9. 19)
(9. 19)
є рівнянням гармонійного коливання, а вираз
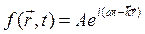 (9.20)
(9.20)
є рівнянням плоскої хвилі.
Використання комплексних чисел для опису коливних та хвильових процесів дозволяє у ряді задач спростити і скоротити розрахунки. Покажемо це на прикладі вимушених коливань.
Виходимо із рівняння руху (7.50) для вимушених коливань, в якому вираз для вимушуючої сили 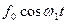 замінимо виразом
замінимо виразом 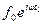 :
:
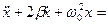
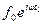 (9. 21)
(9. 21)
Розв’язок рівняння для встановлених коливань шукаємо у вигляді
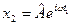 , (9.22)
, (9.22)
де 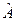 – деяка стаціонарна незалежна від часу амплітуда у вигляді комплексного числа. Підстановка виразу (9.22) у рівняння (9.21) дає наступний результат:
– деяка стаціонарна незалежна від часу амплітуда у вигляді комплексного числа. Підстановка виразу (9.22) у рівняння (9.21) дає наступний результат:
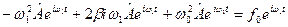 .
.
Скоротивши вираз на 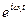 для
для 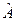 отримаємо:
отримаємо:
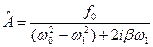 (9. 23)
(9. 23)
Перетворимо знаменник у виразі (9.23), використавши формулу Ейлера, до вигляду:
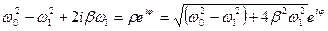 ,
,
де 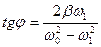 .
.
Тому 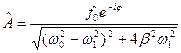 .
.
Кінцево розв’язок рівняння (9. 21) набуває вигляду:
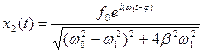 (9.24 )
(9.24 )
З (9.24) видно, що вимушене коливання за фазою відстає від вимушуючої сили на кут 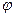 . Отриманий результат ідентичний виразу (7.53).
. Отриманий результат ідентичний виразу (7.53).
[1] Доведемо, що 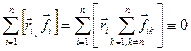 .
.
Згідно з третім законом Ньютона 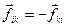 , а тому для доведення записаної вище рівності достатньо показати, що
, а тому для доведення записаної вище рівності достатньо показати, що 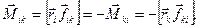 . Запишемо
. Запишемо 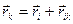 , де
, де 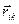 –вектор, що з’єднує точки
–вектор, що з’єднує точки 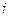 та
та 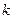 , тоді:
, тоді:
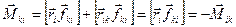 , бо
, бо 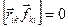 , внаслідок колінеарності векторів
, внаслідок колінеарності векторів 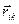 та
та 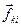 .
.
[2] Дане твердження випливає з того, що кут 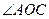 малий (
малий ( 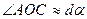 ), а тому
), а тому 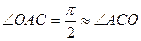 і трикутник
і трикутник 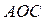 рівнобедрений з рівними сторонами
рівнобедрений з рівними сторонами 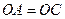 .
.
[3] Відзначимо, що середні значення функції  та
та 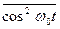 за період рівні 1/2:
за період рівні 1/2: 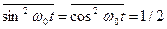 .
.
[4] 
[5] Адіабатичний процес – процес, що відбувається без обміну теплом із зовнішнім середовищем. Ідеальних адіабатичних процесів в природі немає. Адіабатичними процесами можуть вважатись лише швидкозмінні процеси (в даному випадку пружні деформації в хвилі).
Дата добавления: 2015-09-11; просмотров: 940;
