Перелік лабораторних робіт з механіки

1. Визначення густини тіл правильної геометричної форми (№101)

2. Вивчення обертального руху на маятнику Обербека (№111)

3. Дослідження залежності моменту інерції дволанкової системи від її геометричних розмірів (№113)

4. Дослідна перевірка закону збереження моменту імпульсу (№114)

5. Визначення прискорення вільного падіння за допомогою фізичного маятника (№115)

6. Дослідна перевірка теореми Гюйгенса-Штейнера (№116)

7. Дослідження коливань маятника з рухомою точкою підвісу (№117)

8. Дослідження процесу пружної деформації розтягу дротини (№118)

9. Визначення модуля зсуву динамічним методом (№120)

10. Дослідження процесу пружної деформації кручення (№120а)

11. Перевірка теореми Гюйгенса-Штейнера за допомогою трифілярного підвісу (№121)

12. Вивчення коливних процесів (№122)

13. Дослідження прецесії гіроскопа та визначення його моменту інерції (№123)

14. Визначення швидкості польоту кулі балістичним методом (№124)

15. Визначення швидкості звуку в повітрі методом стоячої хвилі (№125)

16. Дослідження коливної системи з двома ступенями вільності (№126)

17. Визначення коефіцієнта тертя кочення (№127)

18. Дослідна перевірка рівняння Бернуллі (№128)

19. Визначення швидкості польоту кулі за допомогою крутильно-балістичного маятника (№129)

20. Визначення швидкості звуку і модуля Юнга в твердих тілах (№130)

ЗРАЗОК

оформлення звіту про виконану роботу

1. Титульна сторінка:

Львівський національний університет імені Івана Франка

Кафедра фізичної і біомедичної електроніки

ЗВІТ

про виконання лабораторної роботи № ...

................(назва роботи).............................

студента..………

Факультет……..

Група....……….

Викладач……….

2. На наступних сторінках потрібно висвітлити:

завдання,

перелік обладнання,

рисунок установки,

робочу формулу з розшифруванням величин, які є в ній,

робочі таблиці,

формули для обчислення похибок,

кінцевий результат,

висновки.

Вступ. Основні поняття класичної механіки

Класична механіка вивчає рух макроскопічних тіл з малими швидкостями v ( v<<c,де с – швидкість поширення світла у вакуумі). Мета класичної механіки – описати рух тіла: в будь-який момент часу вміти знайти положення тіла в просторі, його швидкість та прискорення. Класична механіка складається з таких трьох основних розділів:

1. Кінематика – вивчає закономірності руху тіл не вдаючись в аналіз причин, що викликали цей рух.

2. Динаміка – вивчає закономірності руху тіл, як результат дії на них інших тіл та силових полів.

3. Статика – вивчає умови рівноваги тіл. Закони статики є частковим випадком законів динаміки.

Виявити механічний рух тіла можна лише спостерігаючи зміну положення тіла відносно інших тіл. Під час розгляду механічних явищ користуємось поняттям системи відліку, відносно якої відбувається переміщення тіла. Найчастіше використовують прямокутну (декартову) або одну з полярних (полярна плоска, циліндрична або сферична) систем відліку.

За даного розгляду основними об’єктами дослідження є матеріальна точка та абсолютно тверде тіло.

Матеріальною точкою називають тіло масою m, розмірами якого в умовах даної задачі можна нехтувати.

Макроскопічне тіло, деформаціями якого в умовах даної задачі можна нехтувати, називають абсолютно твердим тілом.

1 Основи кінематики

1.1 Кінематика матеріальної точки

Положення матеріальної точки в просторі задаємо її координатами (x, y, z – в декартовій системі координат) або її радіус-вектором .Радіус-вектор –цевектор, що з’єднує початок системи координат з даною матеріальною точкою. Вектор , як і координати (x, y, z), однозначно описує положення точки в просторі, бо

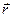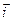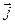= x + y + 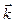z, (1.1)

де 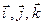– орти, вектори одиничної довжини за напрямками x, y, z відповідно.

Лінію, вздовж якої здійснює переміщення матеріальна точка в просторі, називають траєкторією. В залежності від вигляду траєкторії розглядають рух прямолінійний та криволінійний. Приріст радіус-вектора матеріальної точки – вектор переміщення 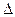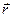(Рис.1). Довжину ділянки траєкторії, що відповідає даному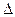 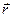називають шляхом S. За прямолінійного або нескінчено малого криволінійного переміщення 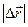= S .

Швидкість 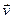– векторна величина: 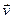= 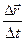, фізичний сенс якої полягає в тому, що вона дорівнює приросту радіуса-вектора за одиницю часу. Розрізняють швидкість миттєву 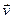= 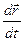, середню на деякій ділянці шляху <v>= 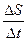(остання є величиною скалярною).

Рух називають рівномірним, якщо модуль швидкості сталий 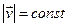, в іншому випадку, рух буде змінним.

Зокрема, криволінійний рух є змінним, бо навіть при 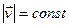, напрямок 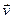неперервно змінюється.

Зміну швидкості з часом характеризує прискорення 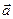, що має сенс зміни вектора 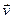за одиницю часу: 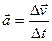, зокрема, миттєве прискорення .

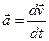Криволінійний рух характеризуємо повним прискоренням 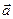, що має дві взаємно перпендикулярні складові: тангенціальне прискорення 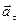(описує зміну модуля вектора 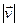і колінеарне напрямку руху) та нормальне 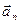( 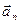перпендикулярне до 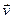і визначає зміну напрямку руху):

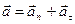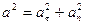, (1.2)

Для аналітичного опису криволінійних траєкторій, окремі ділянки цих кривих часто апроксимують відрізками прямих або дугами кіл (чи відрізками парабол або гіпербол). За умови апроксимації дугами кіл використовують закономірності руху матеріальної точки по колу. Ці закономірності наступні. Під час руху по колу роль шляху відіграє кут повороту радіус-вектора j, роль швидкості – кутова швидкість 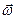, а роль прискорення – кутове прискорення .

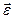За напрямок вектора 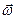беремо напрямок одиничного вектора нормалі до площини, в якій відбувається рух (побудованого за правилом правого гвинта): 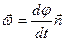, або 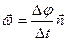. Відповідно для кутового прискорення отримаємо: 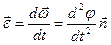. Очевидно, що під час руху по колу вектори 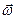і 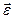паралельні (коли 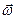зростає з часом) або антипаралельні, (коли обертовий рух сповільнений).

З лінійними швидкістю 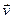та прискоренням 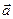матеріальної точки величини 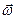і 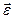пов’язані наступними співвідношеннями:

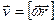, або 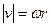(під час руху по колу, 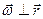). Відповідно

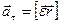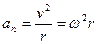, (1.3)

і повне прискорення:

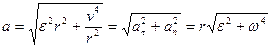, (1.4)

Для характеристики обертального руху використовують також період обертання T – час здійснення одного повного оберту та частоту обертання n – кількість обертів, які виконує тіло за одиницю часу. Згадані величини звичайно використовують під час рівномірного руху по колу, а їх взаємозв’язок з кутовою швидкістю наступний:

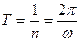(1.5)

Таким чином, характеризувати прямолінійний та обертальний рухи матеріальної точки можна виразами наступного вигляду:

	Рух по прямій	Рух по колу
Рівномірний рух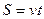
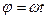
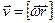
Рівнозмінний рух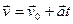
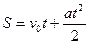
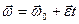
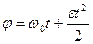
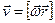
Змінний рух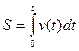

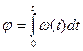
1.2 Елементи кінематики абсолютно твердого тіла

Рух макроскопічного тіла можна розглядати як сукупність рухів окремих його частинок. Тому найпростішим є розгляд руху абсолютно твердого тіла, оскільки в такому тілі відсутні взаємні переміщення частинок тіла. Найпростішим випадком руху абсолютно твердого тіла є поступальний рух (аналог прямолінійного руху матеріальної точки), під час якого будь яка пряма ліня, яка з’єднує довільні точки тіла залишається паралельною сама до себе. Рух тіла називається плоским, якщо кожна точка тіла рухається в одній з паралельних площин. Обертальним рухом твердого тіла – називають такий рух, під час якого траєкторії всіх часток тіла є колами з центрами, розміщеними на одній прямій.

В загальному випадку рух тіла може бути достатньо складним, а тому для спрощення розгляду його намагаються представити як суперпозицію поступального та обертового рухів. За цих умов миттєву швидкість руху 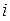-тої матеріальної точки тіла можна записати у вигляді суми двох складових

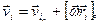(1.5)

де 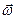- кутова швидкість обертання, 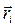- координата 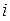- тої точки відносно центра обертання.

Даний підхід не дає однозначної картини. Зокрема, кочення однорідного диска можна представити як у вигляді суми поступального (з швидкістю 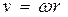) і обертального (з кутовою швидкістю 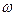) рухів, так і у вигляді лише обертання відносно так званої миттєвої осі, що лежить у тоці дотику диска до поверхнї, по якій він котиться.

Рух абсолютно твердого тіла часто характеризують числом його ступенів вільності, тобто кількістю незалежних координат, що повністю описують його рух. В загальному випадку число ступенів вільності абсолютно твердого тіла не може перевищувати 6 (три поступальні ступені вільності, яким відповідають координати x, y, z та три обертові, яким відповідають кутові швидкост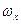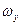і , і 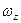відносно трьох взаємно перпендикулярних осей).