Коливання фізичного маятника
Фізичний маятник – тверде тіло, що коливається під дією сили земного тяжіння довкруги горизонтальної осі О, що не проходить через центр мас тіла С. На виведене з рівноваги (відхилене на кут 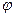 ) тіло діє складова сили тяжіння
) тіло діє складова сили тяжіння 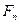 , що створює момент сили, який намагається повернути тіло в положення рівноваги. В даному випадку відсутня сила пружності, однак внесок згаданої складової сили тяжіння подібний за своєю дією пружній силі (квазіпружна сила):
, що створює момент сили, який намагається повернути тіло в положення рівноваги. В даному випадку відсутня сила пружності, однак внесок згаданої складової сили тяжіння подібний за своєю дією пружній силі (квазіпружна сила):

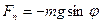
Момент сили створений 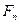 перпендикулярний до площини рисунка і викликає рух за напрямком руху годинникової стрілки:
перпендикулярний до площини рисунка і викликає рух за напрямком руху годинникової стрілки:
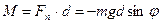
де 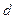 - відстань від точки підвісу О до центра мас С.
- відстань від точки підвісу О до центра мас С.
Рівняння руху маятника можна записати у вигляді аналогічному (2.10а):
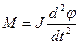
де 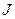 - момент інерції тіла відносно точки О.
- момент інерції тіла відносно точки О.
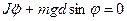 (7.20)
(7.20)
Для малих коливань, коли 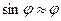 , вираз можна звести до вигляду:
, вираз можна звести до вигляду:
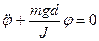 ,
,
або:
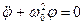 (7.21)
(7.21)
Розв’язком рівняння (7.21) є функція:
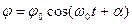 (7.22)
(7.22)
в якій 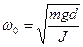 , а період коливань
, а період коливань
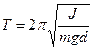 (7.23)
(7.23)
Вираз (7.23) можна звести до вигляду аналогічному виразу (7.18), ввівши позначення 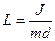 :
:
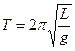 (7.24)
(7.24)
Тут 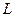 - зведена довжина фізичного маятника, рівна довжині такого математичного маятника, період коливання якого рівний періоду коливання даного фізичного маятника.
- зведена довжина фізичного маятника, рівна довжині такого математичного маятника, період коливання якого рівний періоду коливання даного фізичного маятника.
Особливістю фізичного маятника є те, що на продовженні осі ОС існує точка О', яка ставши новим місцем підвісу осі обертання забезпечує період коливання рівний періоду коливання відносно осі О. Такий фізичний маятник називають оборотним.
7.4 Додавання коливань
У багатьох випадках тіла приймають одночасно участь в декількох коливних рухах. Тому цікавими є задачі, присвячені розрахунку аналітичних виразів, що описують сумарні коливання. Розглянемо деякі типові задачі такого розрахунку.
7.4.1 Додавання коливань однакового напрямку
а) Додавання коливань однакової частоти
Для розв’язку даної задачі звичайно використовують метод вектора амплітуди (метод векторних діаграм). Суть методу полягає в наступному. Довільне гармонійне коливання 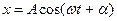 зображаємо графічно з допомогою вектора амплітуди.
зображаємо графічно з допомогою вектора амплітуди.
 З точки О (див. рис. 38) проведемо вектор А довжиною рівною амплітуді під кутом
З точки О (див. рис. 38) проведемо вектор А довжиною рівною амплітуді під кутом 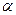 до осі
до осі 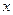 . При обертанні вектора проти напрямку руху годинникової стрілки з кутовою швидкістю
. При обертанні вектора проти напрямку руху годинникової стрілки з кутовою швидкістю 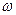 в будь-який момент часу
в будь-який момент часу 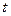 проекція вектора на вісь
проекція вектора на вісь 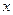 дасть миттєве значення
дасть миттєве значення 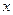 , характерне коливанню
, характерне коливанню 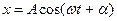 .
.
Якщо необхідно додати декілька коливань, ( 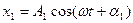 ;
; 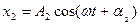 ;
; 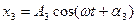 і т. д.), то для цього достатньо додати їх вектори амплітуди і знайти вектор амплітуди сумарного коливання. Проілюструємо це з допомогою додавання двох коливань (див. рис. 39).
і т. д.), то для цього достатньо додати їх вектори амплітуди і знайти вектор амплітуди сумарного коливання. Проілюструємо це з допомогою додавання двох коливань (див. рис. 39).
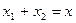
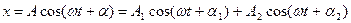
Амплітуду сумарного коливання знаходимо за теоремою косинусів, а 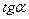 - з розгляду прямокутного трикутника.
- з розгляду прямокутного трикутника.
При додаванні більшого числа коливань зручно користуватись геометричною побудовою сумарного вектора амплітуди і графічного визначення сумарних 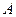 та
та 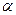 .
.
 |
б) Додавання коливань з близькими частотами. Биття
Розглянемо додавання двох гармонійних коливань однакової амплітуди ( 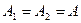 ) з частотами
) з частотами 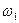 і
і 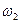 :
:
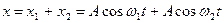
Елементарний аналітичний розрахунок для сумарного коливання дає наступний вираз:
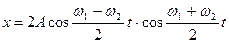 (7.25)
(7.25)
 |
Отриманий вираз описує коливання частотою
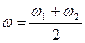 , амплітуда якого
, амплітуда якого 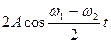 повільно змінюється з частотою
повільно змінюється з частотою 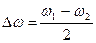 меншою за
меншою за 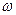 .
.
Якщо частоти коливань 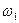 і
і 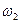 близькі між собою, то виникає явище, яке називають биттям. В цьому випадку частота
близькі між собою, то виникає явище, яке називають биттям. В цьому випадку частота 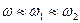 , а
, а 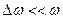 . В результаті виникає коливання з пульсуючою амплітудою (див. рис. 40).
. В результаті виникає коливання з пульсуючою амплітудою (див. рис. 40).
7.4.2 Додавання взаємно перпендикулярних коливань
Розглянемо рух матеріальної точки, яка одночасно приймає участь у декількох коливних рухах в різних напрямках. Найпростішою задачею даного плану є задача додавання двох взаємно перпендикулярних коливань однакової частоти 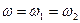 .
.
Нехай матеріальна точка одночасно виконує коливання: 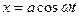 і
і 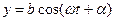 ,
, 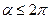 . Знайдемо рівняння траєкторії результуючого руху. Для цього з обох рівнянь виключимо час
. Знайдемо рівняння траєкторії результуючого руху. Для цього з обох рівнянь виключимо час 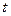 і знайдемо взаємозв’язок між
і знайдемо взаємозв’язок між 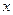 і
і 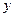 .
.
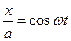 ;
; 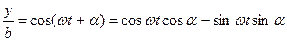 (7.26)
(7.26)
Врахуємо, що 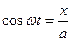 , а
, а 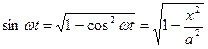 і підставимо їх у вираз
і підставимо їх у вираз
( 7.26):
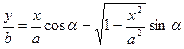
Після перетворення останнього виразу отримаємо:
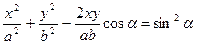 (7.27)
(7.27)
Вираз (7.27) є рівнянням еліпса, орієнтованого довільно відносно осей 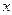 та
та 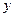 . Дослідимо форму траєкторії в декількох часткових випадках:
. Дослідимо форму траєкторії в декількох часткових випадках:
а) При 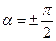 , рівняння (7.27) набуває вигляду:
, рівняння (7.27) набуває вигляду:
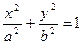 (7.28)
(7.28)
Вираз (7.28) є рівнянням еліпса, півосі якого співпадають з осями 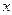 і
і 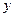 . Див. рис. 41.
. Див. рис. 41.
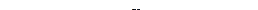 Коли математичний маятник одночасно виконує коливання в напрямках
Коли математичний маятник одночасно виконує коливання в напрямках 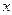 і
і 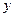 , то матеріальна точка, що є складовою маятника рухається траєкторією, зображеною на рис. 41. У випадку рівності амплітуд
, то матеріальна точка, що є складовою маятника рухається траєкторією, зображеною на рис. 41. У випадку рівності амплітуд 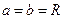 , еліптична траєкторія руху вироджується в коло.
, еліптична траєкторія руху вироджується в коло.
б) При 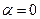 ;
; 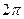 вираз (7.27)набуває вигляду:
вираз (7.27)набуває вигляду:
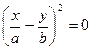 (7.29)
(7.29)
З цього виразу отримаємо 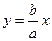 (див. рис. 42).
(див. рис. 42).
Тіло рухається по прямій з кутовим коефіцієнтом 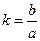 . Максимальне відхилення точки в напрямку цієї прямої
. Максимальне відхилення точки в напрямку цієї прямої 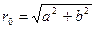 .
.
 Рівняння коливання вздовж прямої
Рівняння коливання вздовж прямої 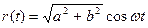 .
.
в) При 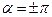 вираз (7.27) набуває вигляду:
вираз (7.27) набуває вигляду:
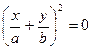 (7.30)
(7.30)
або 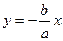 (див. рис. 43).
(див. рис. 43).
 Результуючим рухом буде коливний рух по прямій з кутовим коефіцієнтом
Результуючим рухом буде коливний рух по прямій з кутовим коефіцієнтом 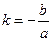 .
.
При 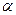 відмінних від 0,
відмінних від 0, 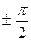 ;
; 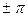 та
та 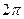 траєкторія руху буде еліпс, орієнтація якого відносно
траєкторія руху буде еліпс, орієнтація якого відносно 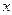 і
і 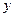 визначається кутом
визначається кутом 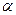 .
.
При додаванні взаємно перпендикулярних коливань з різними частотами  результуючими траєкторіями є криві складних форм, які називають фігурами Лісажу. Вигляд цих кривих суттєво залежить як від співвідношення між частотами коливань так і від початкової різниці фаз коливань.
результуючими траєкторіями є криві складних форм, які називають фігурами Лісажу. Вигляд цих кривих суттєво залежить як від співвідношення між частотами коливань так і від початкової різниці фаз коливань.
Відносно прості фігури Лісажу отримуються при додаванні коливань, частоти яких кратні. Для прикладу на рис. 44 показані фігури Лісажу, що отримуються при додаванні коливань з різними відношеннями частот і різною різницею початкових фаз коливань.
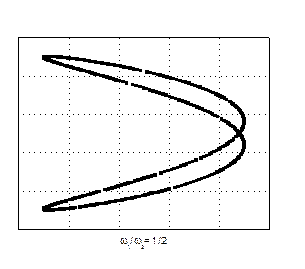
| 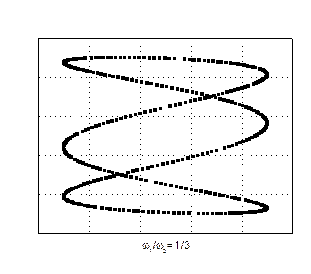
|
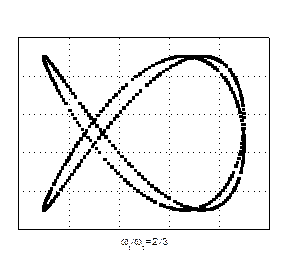
| 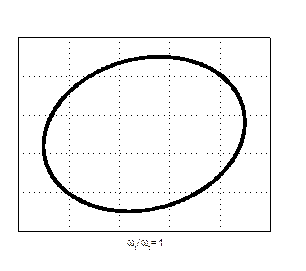
|
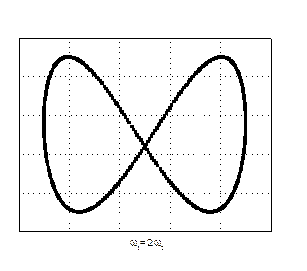
| 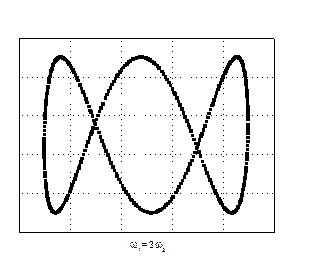
|
|
7.5 Коливання при наявності сил опору середовища. Згасаючі коливання та їх характеристики
В реальних коливних системах завжди діють сили тертя і опору середовища. Тому мають місце втрати енергії на подолання цих сил, а також на збудження коливань у навколишньому середовищі. Усе це призводить до зменшення енергії коливань, що проявляється у зменшенні амплітуди коливань, оскільки енергія коливання пропорційна квадрату амплітуди: 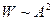 . Коливання, які відбуваються при поступовій втраті їх енергії називаються згасальними.
. Коливання, які відбуваються при поступовій втраті їх енергії називаються згасальними.
При розгляді коливних процесів у попередніх параграфах використовувались припущення про невеликі відхилення систем від положення рівноваги. Тому при аналізі впливу сил тертя на коливні процеси з достатньою достовірністю можна вважати, що дані процеси відбуваються з малими швидкостями і величина сили опору (тертя) пропорційна швидкості:
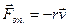 (7.31)
(7.31)
З урахуванням сили тертя рівняння руху одномірної коливної системи може бути записане:
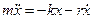 , (7.32)
, (7.32)
або
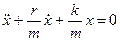
Введемо позначення 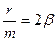 та
та 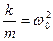 і запишемо рівняння руху:
і запишемо рівняння руху:
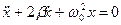 (7.33)
(7.33)
Розв’язок рівняння (7.33) шукаємо у вигляді:
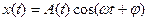 (7.34)
(7.34)
Вважаємо, що вплив сил тертя призводить до зменшення амплітуди коливань з часом: 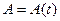 . Підставимо шуканий розв’язок (7.34) у рівняння (7.33) і отримаємо[4]:
. Підставимо шуканий розв’язок (7.34) у рівняння (7.33) і отримаємо[4]:
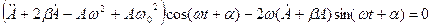 (7.35)
(7.35)
Вираз (7.35) тотожно дорівнює нулю, коли коефіцієнти при 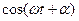 та
та 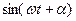 дорівнюють нулю. Тому:
дорівнюють нулю. Тому:
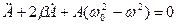 (7.36)
(7.36)
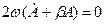 (7.37)
(7.37)
Оскільки 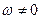 , то розв’язок рівняння (7.37) зводиться до наступного:
, то розв’язок рівняння (7.37) зводиться до наступного:
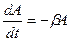 ,
,
або 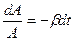 .
.
Проінтегруємо останній вираз і отримаємо:
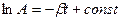 , або
, або 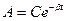 .
.
Постійну інтегрування знаходимо з початкової умови. Нехай при 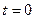 амплітуда коливань дорівнює
амплітуда коливань дорівнює 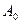 , тоді
, тоді 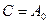 і
і
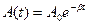 (7.39)
(7.39)
З виразу (7.39) видно, що амплітуда коливань при наявності опору середовища зменшується за експоненціальним законом.
Підставимо (7.39) у рівняння (7.36) і отримаємо:
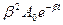 +(
+( 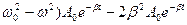 =0
=0
Скоротивши вираз на 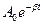 , знайдемо невідому величину
, знайдемо невідому величину 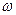 :
:
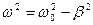 ,
,
або 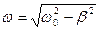 (7.40)
(7.40)
Кінцево розв’язок рівняння (7.33) набуває вигляду (рис. 45):
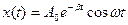 (7.41)
(7.41)
 |
Таким чином, частота коливань системи при наявності опору середовища менша за частоту коливань системи без втрат. Це зменшення частоти тим більше, чим більший коефіцієнт, що характеризує опір середовища: 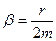 і
і 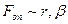 . Зокрема, при значних силах тертя, коли
. Зокрема, при значних силах тертя, коли 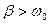 , з виразу (7.40) одержується уявне значення
, з виразу (7.40) одержується уявне значення 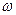 . Це свідчить про те, що у системі відсутні періодичні коливні рухи і є лише неперіодичне повернення системи до положення рівноваги (рис. 46).
. Це свідчить про те, що у системі відсутні періодичні коливні рухи і є лише неперіодичне повернення системи до положення рівноваги (рис. 46).
Характеристики згасальних коливань.
1. Коефіцієнт згасання 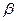 – величина обернена часу
– величина обернена часу 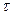 , протягом якого амплітуда коливання зменшиться в
, протягом якого амплітуда коливання зменшиться в 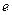 разів:
разів:
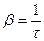 (7.42)
(7.42)
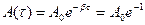
2. Декремент згасання 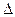 – відношення двох послідовних амплітуд:
– відношення двох послідовних амплітуд:
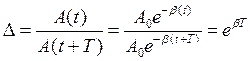 (7.43)
(7.43)
3. Логарифмічний декремент згасання:
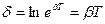
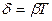 (7.44)
(7.44)
Величина обернена до 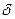 дорівнює кількості коливань, протягом яких амплітуда коливань зменшиться в
дорівнює кількості коливань, протягом яких амплітуда коливань зменшиться в 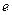 разів:
разів:
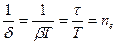 (7.45)
(7.45)
4. Добротність коливної системи:
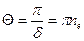 , (7.46)
, (7.46)
яка характеризує енергетичні втрати системи за один період.
Відомо, що енергія коливної системи пропорційна квадрату амплітуди. Тому закон зменшення енергії коливань можна записати:
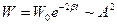 , (7.47)
, (7.47)
де 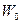 – енергія коливання при
– енергія коливання при 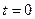 . Швидкість наростання енергії з часом дорівнює
. Швидкість наростання енергії з часом дорівнює 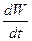 , а
, а 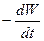 – швидкість спадання енергії коливань:
– швидкість спадання енергії коливань: 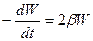 .
.
Якщо згасання коливань мале, то зміна енергії коливань за період 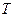 приблизно дорівнює:
приблизно дорівнює:
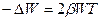 ,
,
або 
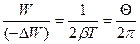 (7.48)
(7.48)
Тобто при незначному згасанні 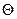 з точністю до множника
з точністю до множника 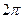 дорівнює відношенню енергії коливної системи в даний момент до втрати енергії за один період.
дорівнює відношенню енергії коливної системи в даний момент до втрати енергії за один період.
7.6 Вимушені коливання
Всяке реальне вільне коливання з часом згасає. Для підтримання коливань протягом тривалого часу необхідно постійно поповнювати енергію коливної системи. Це можна здійснити шляхом дії на систему зовнішньої періодичної сили.
Якщо на систему крім пружної сили 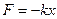 та сили опору
та сили опору 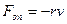 діє зовнішня періодична вимушуючи сила
діє зовнішня періодична вимушуючи сила 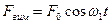 , то коливання в системі, що існують протягом тривалого часу, називають вимушеними.
, то коливання в системі, що існують протягом тривалого часу, називають вимушеними.
Рівняння руху одномірної коливної системи в даному випадку можна записати в наступному вигляді:
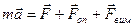 ,
,
або
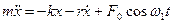 (7.49)
(7.49)
Введемо позначення 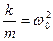 ;
; 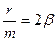 ,
, 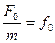 і кінцево отримаємо рівняння руху системи:
і кінцево отримаємо рівняння руху системи:
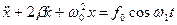 (7.50)
(7.50)
Рівняння типу (7.50) називають неоднорідним нелінійним диференціальним рівнянням другого порядку. Загальний розв’язок такого рівняння складається з загального розв’язку відповідного однорідного рівняння (7.33) і часткового розв’язку неоднорідного рівняння (7.50). Загальний розв’язок однорідного рівняння (тобто рівняння, в якому права сторона дорівнює нулю) дається виразом (7.41): 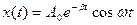 . Ці власні коливання системи виникають у початковий проміжок часу дії вимушуючої сили, однак при тривалій дії вимушуючої сили (
. Ці власні коливання системи виникають у початковий проміжок часу дії вимушуючої сили, однак при тривалій дії вимушуючої сили ( 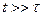 , де
, де 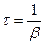 ) власні коливання практично згасають.
) власні коливання практично згасають.
На початку своєї дії вимушуюча сила перевищує силу тертя, а тому робота цієї сили сприяє збільшенню кінетичної енергії коливань та їх амплітуди. Із зростанням енергії коливань поступово збільшується сила тертя (величина сили тертя пропорційна швидкості) і кінцево настає стабілізація вимушених коливань, при якій дія сили тертя зрівноважується вимушуючою силою і коливання стають стабільними. Процес встановлення вимушених коливань схематично показано на рис. 47.
 Знайдемо амплітуду
Знайдемо амплітуду 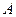 встановлених (стабільних) вимушених коливань та їх зсув фази по відношенню до фази вимушуючого коливання. Вважаємо, що вимушене коливання відстає за фазою від вимушуючої сили на кут
встановлених (стабільних) вимушених коливань та їх зсув фази по відношенню до фази вимушуючого коливання. Вважаємо, що вимушене коливання відстає за фазою від вимушуючої сили на кут 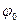 . Частковий розв’язок неоднорідного рівняння шукаємо у вигляді:
. Частковий розв’язок неоднорідного рівняння шукаємо у вигляді:
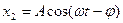 (7.51)
(7.51)
Підставимо цей розв’язок у рівняння руху (7.50) і розв’яжемо рівняння, використавши метод векторних діаграм:
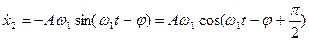
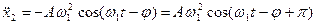
Після підстановки 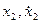 та
та 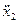 у (7.50) отримаємо:
у (7.50) отримаємо:
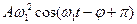 +
+ 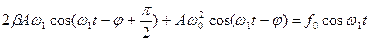
Таким чином, гармонійна функція 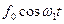 може бути виражена як сума трьох гармонійних коливань, які можна зобразити як три вектори, повернуті один відносно одного на кут
може бути виражена як сума трьох гармонійних коливань, які можна зобразити як три вектори, повернуті один відносно одного на кут 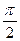 . Вектор амплітуди вимушуючої сили
. Вектор амплітуди вимушуючої сили 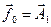 дорівнює векторній сумі векторів:
дорівнює векторній сумі векторів:
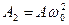 (зсунутий по фазі відносно
(зсунутий по фазі відносно 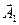 на кут –
на кут – 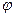 )
)
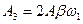 (випереджає
(випереджає 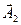 на кут
на кут 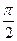 ) і
) і
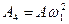 (випереджає
(випереджає 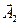 на кут p ).
на кут p ).
 |
У прямокутному трикутнику ОВД вектор
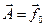 є гіпотенузою:
є гіпотенузою:
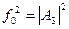 +
+ 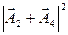
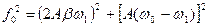
З цього виразу амплітуда вимушених коливань:
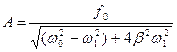 (7.51)
(7.51)
і 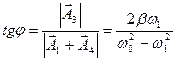 (7.52)
(7.52)
Таким чином, рівняння вимушених коливань має наступний вигляд
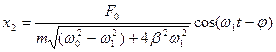 , (7.53)
, (7.53)
в якому відставання за фазою вимушених коливань 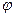 дається (7.52).
дається (7.52).
Проаналізуємо більш детально залежність виразу (7.53) від кругової частоти вимушуючої сили 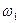 .
.
1. При 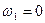 на систему діє стаціонарна сила
на систему діє стаціонарна сила 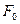 .
.
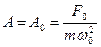 .
.
Зміщення системи під дією стаціонарної сили відповідає статичній деформації
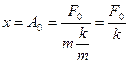 (7.54)
(7.54)
2. При відсутності сил опору середовища ( 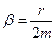 =0) вираз (7.51) набуває вигляду:
=0) вираз (7.51) набуває вигляду:
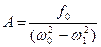 (7.55)
(7.55)
Із збільшенням кругової частоти 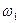 від
від 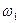 = 0 амплітуда коливань зростає, прямуючи до нескінченості при
= 0 амплітуда коливань зростає, прямуючи до нескінченості при 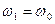 . Коли
. Коли 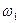 перевищує
перевищує 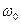 збільшення кругової частоти
збільшення кругової частоти 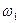 вимушуючої сили веде до зменшення амплітуди коливань (рис. 49).
вимушуючої сили веде до зменшення амплітуди коливань (рис. 49).
3. При наявності сил тертя 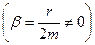 на залежності амплітуди вимушених коливань
на залежності амплітуди вимушених коливань 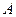 від кругової частоти
від кругової частоти 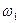 існує максимум, що відповідає мінімальному значенню підкореневого виразу в (7.51). Для цього прирівняємо до нуля похідну підкореневого виразу по
існує максимум, що відповідає мінімальному значенню підкореневого виразу в (7.51). Для цього прирівняємо до нуля похідну підкореневого виразу по 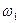 і отримаємо:
і отримаємо:
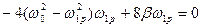 , (7.56)
, (7.56)
де 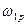 – кругова частота вимушуючої сили, при якій амплітуда вимушених коливань набуває максимального значення
– кругова частота вимушуючої сили, при якій амплітуда вимушених коливань набуває максимального значення 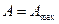 . З (7.56) отримуємо:
. З (7.56) отримуємо:
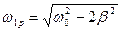 (7.57)
(7.57)
Амплітуда коливань у максимумі дорівнює:
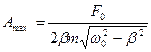 (7.58)
(7.58)
Явище наростання амплітуди коливань при наближенні до кругової частоти 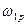 називається резонансом, а частоту
називається резонансом, а частоту 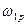 називають резонансною частотою. З виразів (7.57) і (7.58) видно, що резонансна кругова частота
називають резонансною частотою. З виразів (7.57) і (7.58) видно, що резонансна кругова частота 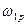 та амплітуда вимушених коливань у резонансі
та амплітуда вимушених коливань у резонансі 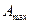 залежать від величини сил тертя: із збільшенням сил опору обидві величини зменшуються. Очевидним є те, що при
залежать від величини сил тертя: із збільшенням сил опору обидві величини зменшуються. Очевидним є те, що при 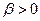 резонансна кругова частота завжди менша за
резонансна кругова частота завжди менша за 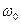 :
: 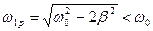 . При відсутності сил опору в ідеальній системі без втрат
. При відсутності сил опору в ідеальній системі без втрат 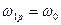 . Криві залежності
. Криві залежності 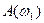 називають амплітудними резонансними кривими (рис. 49).
називають амплітудними резонансними кривими (рис. 49).
 |
При кругових частотах
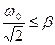 явище резонансу зникає.
явище резонансу зникає.
Проаналізуємо залежність відставання по фазі 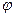 вимушених коливань від частоти вимушуючої сили
вимушених коливань від частоти вимушуючої сили 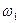 (вираз 7.52). При малих частотах (
(вираз 7.52). При малих частотах ( 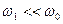 )
) 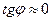 , тобто фаза вимушених коливань співпадає з фазою вимушуючої сили; при наближенні
, тобто фаза вимушених коливань співпадає з фазою вимушуючої сили; при наближенні 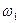 до
до 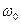 кут
кут 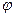 поступово зростає, досягаючи
поступово зростає, досягаючи 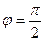 при
при 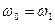 . При подальшому збільшенні частоти (
. При подальшому збільшенні частоти ( 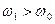 )
) 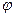 поступово зростає, досягаючи значення
поступово зростає, досягаючи значення 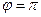 при
при 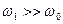 . Залежності
. Залежності 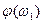 називають фазовими кривими резонансу (див. рис. 50).
називають фазовими кривими резонансу (див. рис. 50).
 |
Нагадаємо, що явище резонансу може бути корисним і шкідливим. Зокрема, в механіці резонансні явища використовують для аналізу звуку в акустиці, для підсилення акустичних коливань з допомогою резонаторів. У багатьох механічних системах резонансні явища шкідливі і у ряді випадків можуть призвести до руйнування об’єкта (коливання крил літаків, мостів, у лініях електропередач, у висотних об’єктах).
7.7 Параметричне збудження коливань
Збудження вимушених коливань можливе не лише за рахунок введення у коливну систему енергії, яка безпосередньо спричинює рух коливного тіла, але і за рахунок дії, що лише змінює властивості коливальної системи. Якщо зовнішня дія таким чином змінює параметри системи, що збуджуються коливання, ці коливання називають параметричними.
Розглянемо дане явище на прикладі властивостей математичного маятника, який вже здійснює дуже малі коливання. Параметричну дію на маятник можна здійснити, періодично змінюючи його довжину, тобто втягуючи і випускаючи нитку, на якій висить матеріальна точка масою 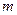 . Втягуючи нитку, ми виконуємо роботу, яка збільшує енергію маятника. При випусканні нитки ми забираємо енергію від маятника. Якщо втягування нитки відбувається у середній точці, а випускання – в крайніх положеннях, коливної системи то позитивна робота в середньому положенні більша за від’ємну в крайніх положеннях. Тому за кожне коливання маятник одержує певну порцію енергії. Тобто збудження вимушених коливань за рахунок зміни параметрів системи можливе, коли ця дія відбувається з відповідними частотою та фазами. Зокрема, частота дії у випадку маятника повинна бути у два рази більшою від частоти власних коливань маятника. Тому це явище деколи називають параметричним резонансом. Відзначимо, що для параметричного збудження коливань принципово необхідно, щоб система вже здійснювала малі коливання.
. Втягуючи нитку, ми виконуємо роботу, яка збільшує енергію маятника. При випусканні нитки ми забираємо енергію від маятника. Якщо втягування нитки відбувається у середній точці, а випускання – в крайніх положеннях, коливної системи то позитивна робота в середньому положенні більша за від’ємну в крайніх положеннях. Тому за кожне коливання маятник одержує певну порцію енергії. Тобто збудження вимушених коливань за рахунок зміни параметрів системи можливе, коли ця дія відбувається з відповідними частотою та фазами. Зокрема, частота дії у випадку маятника повинна бути у два рази більшою від частоти власних коливань маятника. Тому це явище деколи називають параметричним резонансом. Відзначимо, що для параметричного збудження коливань принципово необхідно, щоб система вже здійснювала малі коливання.
7.8 Автоколивання
Власні коливання – коливання навколо положення стійкої рівноваги. Амплітуда цих коливань визначається тією енергією, яка передана тілу початковим поштовхом. Внаслідок дії сил тертя власні коливання згасають і тому не можуть бути стаціонарними. Щоб підтримувати коливання, система повинна мати джерело енергії, яке надасть за період коливання порцію енергії, яка дорівнює тій енергії, що витрачена на подолання сил тертя. Тобто система повинна сама керувати надходженням енергії від джерела. Системи даного типу називають автоколивними, а отримані в них незгасаючі коливання – автоколиваннями.
Типовим прикладом механічної автоколивальної системи є механізм годинника.
Дата добавления: 2015-09-11; просмотров: 5926;
