Коливання в механічних системах
Коливними процесами називають зміни фізичних величин, що відзначаються певною періодичною повторюваністю. Коливні процеси розрізняються за своєю фізичною природою (коливання механічні, електричні, електромеханічні, електромагнітні та ін.), за характером здійснення самих коливань та способом забезпечення коливної системи енергією (коливання власні або вільні, вимушені, параметричні, автоколивання) та за характером часової залежності фізичної величини, за виглядом функціональних залежностей, що їх описують.
Спільною рисою всіх коливних процесів є те, що незалежно від їх природи існують спільні закономірності розгляду та математичні методи дослідження коливань. Зокрема, це в першу чергу стосується опису часових залежностей коливань фізичних величин. В даному розділі розглянемо лише так звані гармонійні коливання, тобто коливання, при яких часова залежність змін фізичних величин описується функціями типу 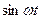 ,
, 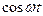 або
або 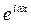 . Увага до розгляду гармонійних коливань зумовлена тим, що довільна періодична функціональна залежність з допомогою рядів Фур’є може бути представлена як суперпозиція гармонічних функцій з кратними частотами. Перетворення даного типу вивчаються математично в гармонійному аналізі.
. Увага до розгляду гармонійних коливань зумовлена тим, що довільна періодична функціональна залежність з допомогою рядів Фур’є може бути представлена як суперпозиція гармонічних функцій з кратними частотами. Перетворення даного типу вивчаються математично в гармонійному аналізі.
7.1 Характеристики гармонійних коливань
Розглянемо механічні гармонійні коливання, тобто зміни фізичної величини 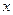 , що описуються функціями:
, що описуються функціями:
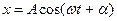 ;
; 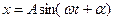 або
або 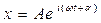 (7.1)
(7.1)
В даних виразах 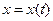 - миттєве значення величини
- миттєве значення величини 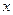 в момент часу
в момент часу 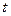 ;
; 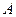 - амплітуда коливань – максимальне значення величини
- амплітуда коливань – максимальне значення величини 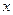 :
: 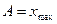 ;
; 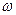 - кругова частота коливань;
- кругова частота коливань; 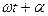 - фаза коливання,
- фаза коливання, 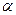 - початкова фаза, яка характеризує миттєвий стан коливної системи в початковий момент часу
- початкова фаза, яка характеризує миттєвий стан коливної системи в початковий момент часу 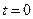 . Період
. Період 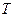 - час, протягом якого здійснюється одне повне коливання і система повертається в початковий стан визначають з наступного співвідношення:
- час, протягом якого здійснюється одне повне коливання і система повертається в початковий стан визначають з наступного співвідношення:
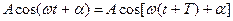 ,
,
або:
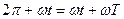
Таким чином взаємозв’язок між періодом і круговою частотою :
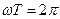 , або
, або 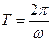 , чи
, чи 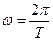 (7.2)
(7.2)
Величина обернена періоду 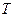 :
: 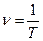 - частота коливань (кількість коливань здійснених за одиницю часу).
- частота коливань (кількість коливань здійснених за одиницю часу).
Взаємозв’язок між круговою частотою 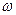 та частотою
та частотою 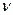 :
:
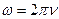 (7.3)
(7.3)
Якщо величину 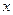 вважати зміщенням системи від положення рівноваги чи координатою матеріальної точки, що здійснює гармонійні коливання, то швидкість і прискорення в коливній системі можна знайти, взявши відповідні похідні по часу від
вважати зміщенням системи від положення рівноваги чи координатою матеріальної точки, що здійснює гармонійні коливання, то швидкість і прискорення в коливній системі можна знайти, взявши відповідні похідні по часу від 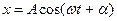 :
:
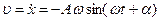 (7.4)
(7.4)
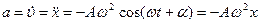 (7.5)
(7.5)
Максимальні значення 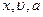 :
: 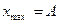 ;
; 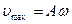 ;
; 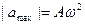 отримуються із зсувом фаз на кут
отримуються із зсувом фаз на кут 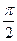 одне від одного.
одне від одного.
Вираз (7.5) можна використати для написання рівняння руху коливної системи. Згідно з другим законом Ньютона для одномірного руху:
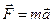 ,
, 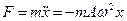 (7.6)
(7.6)
Рівняння 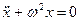 є рівнянням руху одномірної коливної системи (рівнянням одномірного осцилятора). З виразу (7.6) видно, що одномірні коливання виникають під дією сили, яка за своїм аналітичним виразом може бути подана у вигляді:
є рівнянням руху одномірної коливної системи (рівнянням одномірного осцилятора). З виразу (7.6) видно, що одномірні коливання виникають під дією сили, яка за своїм аналітичним виразом може бути подана у вигляді:
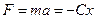 (7.8)
(7.8)
де 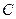 - деяка стала, більша за нуль. Запис даної сили по вигляду аналогічний до запису закону Гука для деформації розтягу (стиску)
- деяка стала, більша за нуль. Запис даної сили по вигляду аналогічний до запису закону Гука для деформації розтягу (стиску) 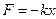 .
.
Можна стверджувати, що гармонійні коливання виникають при русі під дією пружної сили, або під дією сили довільної природи, для якої справедливий вираз, аналогічний до (7.8). Тому силу, що описується виразом (7.8) назвемо квазіпружною.
7.2 Коливання під дією пружної сили. Енергія коливань
Якщо ізольовану систему початково вивести з положення рівноваги дією деформуючої сили, то після ізоляції системи внутрішні сили намагатимуться повернути систему в початковий рівноважний стан. При цьому виникнуть коливання в системі, які називають вільними (власними). Як приклад, розглянемо коливання в системі описаній в 5.3.
Згідно з виразом (5.10) рівняння руху пластини масою 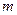 під дією пружної сили:
під дією пружної сили:
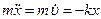 , або
, або
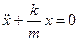 (7.9)
(7.9)
Якщо введемо позначення 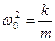 і вираз (7.9) зведеться до вигляду виразу (7.6). По аналогії з попереднім параграфом отримаємо:
і вираз (7.9) зведеться до вигляду виразу (7.6). По аналогії з попереднім параграфом отримаємо:
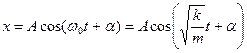 (7.10)
(7.10)
Оцінимо енергію коливань системи. Згідно з (5.12) енергія системи, зображеної на рис.14 дорівнює:
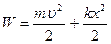
Підставивши у вираз для 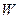 значення
значення 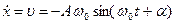 та
та 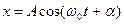 , отримаємо:
, отримаємо:
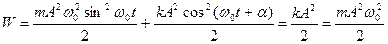 (7.11)
(7.11)
Вираз (7.11) підтверджує, що в коливній системі має місце почергове перетворення потенціальної енергії деформації пружини в кінетичну енергію руху пластини і навпаки:
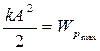 ,
, 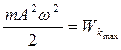 (7.12)
(7.12)
З виразу (7.11) можна показати, що середня кінетична енергія гармонійного коливання дорівнює його середній потенціальній енергії. Для цього слід усереднити вирази 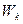 та
та 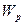 протягом періоду[3]:
протягом періоду[3]:
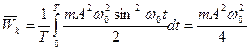
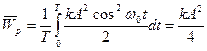
З виразів видно, що 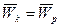 , бо
, бо 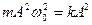 .
.
7.3 Вільні коливання систем під дією пружних та квазіпружних сил
7.3.1 Коливання крутильного маятника
Крутильним маятником називають тіло А з відомим моментом інерції 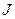 , підвішене на дротині В.
, підвішене на дротині В.
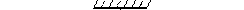 Тіло може виконувати крутильні коливання під дією моменту пружної сили
Тіло може виконувати крутильні коливання під дією моменту пружної сили 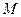 , що виникає при закручуванні дротини:
, що виникає при закручуванні дротини:
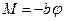 (7.13)
(7.13)
де 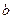 - модуль кручення,
- модуль кручення, 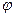 - кут закручування дротини. Рівняння руху системи:
- кут закручування дротини. Рівняння руху системи:
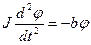 (7.14)
(7.14)
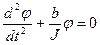
Розв’язок рівняння руху 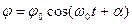 . Тут
. Тут 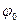 - максимальний (амплітудний) кут закручування дротини,
- максимальний (амплітудний) кут закручування дротини, 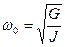 , а період коливань:
, а період коливань:
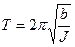 (7.15)
(7.15)
7.3.2 Коливання математичного маятника
Математичним маятником називають матеріальну точку масою 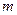 , підвішену на невагомій і нерозтяжній нитці довжиною
, підвішену на невагомій і нерозтяжній нитці довжиною 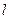 , яка коливається у вертикальній площині під дією сили тяжіння. Коли система перебуває в спокої (матеріальна точка в положенні А), то сила тяжіння
, яка коливається у вертикальній площині під дією сили тяжіння. Коли система перебуває в спокої (матеріальна точка в положенні А), то сила тяжіння 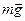 зрівноважується силою натягу нитки
зрівноважується силою натягу нитки 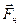 . Якщо матеріальну точку з ниткою відхилити на деякий кут
. Якщо матеріальну точку з ниткою відхилити на деякий кут 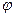 (точка В), то рівнодійна сил натягу і земного тяжіння
(точка В), то рівнодійна сил натягу і земного тяжіння 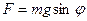 намагається повернути систему в положення рівноваги. Для малих кутів відхилення
намагається повернути систему в положення рівноваги. Для малих кутів відхилення 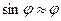 вираз для
вираз для 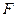 можна записати
можна записати 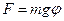 . Дана сила створює обертовий момент сили
. Дана сила створює обертовий момент сили 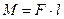 , напрямлений перпендикулярно площині рисунка, який намагається повернути
, напрямлений перпендикулярно площині рисунка, який намагається повернути
 систему в положення рівноваги. Повернення матеріальної точки в положення рівноваги проходить по дузі кола радіуса
систему в положення рівноваги. Повернення матеріальної точки в положення рівноваги проходить по дузі кола радіуса 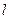 . Рівняння руху матеріальної точки по коловій траєкторії можна записати у вигляді аналогічному (2.10а):
. Рівняння руху матеріальної точки по коловій траєкторії можна записати у вигляді аналогічному (2.10а):
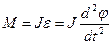 ,
,
врахувавши, що 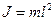 .
.
Таким чином:
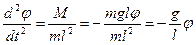 (7.16)
(7.16)
В останньому виразі в правій частині знаком “-” підтверджено, що повертаючий в положення рівноваги обертовий момент діє в напрямку протилежному зростанню кута відхилення 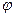 . Кінцево рівняння руху запишеться у вигляді:
. Кінцево рівняння руху запишеться у вигляді:
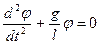 , або
, або 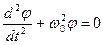 (7.17)
(7.17)
Тут 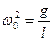 , а період коливань:
, а період коливань:
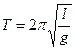 (7.18)
(7.18)
Відзначимо ,що більш точний вираз для періоду коливань математичного маятника можна записати у вигляді:
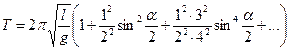 (7.19)
(7.19)
де 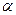 - максимальний кут відхилення маятника. Якщо
- максимальний кут відхилення маятника. Якщо 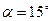 , то відносне відхилення розрахунку періоду за виразом (7.18) від результату отриманого за допомогою (7.19) менше за 0,5%.
, то відносне відхилення розрахунку періоду за виразом (7.18) від результату отриманого за допомогою (7.19) менше за 0,5%.
Дата добавления: 2015-09-11; просмотров: 1136;
