Механіка рідин
Відміна властивостей рідин і газів від властивостей твердих тіл полягає у відсутності у них пружності форми і відсутності опору деформації зсуву. Їм властива лише пружність об’єму. Тому в рідині або газі існує лише пружна деформація стиску. В результаті цього у стані рівноваги в них існують напруження, перпендикулярні до поверхні, на яку вони діють. Закони механіки, що описують властивості рідин і газів, подібні між собою, а тому будемо говорити про рідину, пам’ятаючи, що отримані висновки справедливі і для газів. Рухливість частинок рідин і газів відносно велика, а під час руху елементи їхніх мас змінюють своє взаємне розташування.
Механіка рідин складається з двох основних розділів:
1. Гідростатика –вивчає умови рівноваги рідин під впливом прикладених сил і дію рідин на занурені у них тверді тіла та стінки посудини.
2. Гідродинаміка – вивчає рух рідин та механічну взаємодію між рідиною і твердим тілом при їх взаємному русі.
6.1 Закони гідростатики
З точки зору механіки рідини є середовищами, у яких при рівновазі дотичні напруження існувати не можуть. Тому в стані рівноваги тиск на площадку 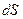 довільної орієнтації завжди нормальний до її поверхні (тобто
довільної орієнтації завжди нормальний до її поверхні (тобто 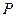 ^
^ 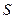 ). З цього випливає закон Паскаля, який стверджує, що у стані спокою тиск у даній точці рідини однаковий в усіх напрямках. Дія різних гідравлічних пристроїв базується на висновках з цього закону.
). З цього випливає закон Паскаля, який стверджує, що у стані спокою тиск у даній точці рідини однаковий в усіх напрямках. Дія різних гідравлічних пристроїв базується на висновках з цього закону.
Закон Паскаля строго справедливий, якщо на рідину не діють зовнішні сили. У полі зовнішніх сил на всі частинки рідини діють сили у напрямку дії сил поля. Зокрема, якщо трубу (рис. 19) довжиною 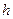 і перерізом
і перерізом 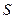 заповнити рідиною і встановити систему вертикально,
заповнити рідиною і встановити систему вертикально,  то на усі частинки рідини діятиме сила тяжіння, величина якої залежить від маси рідини:
то на усі частинки рідини діятиме сила тяжіння, величина якої залежить від маси рідини: 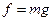 . На верхній шар рідини товщиною
. На верхній шар рідини товщиною 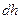 діє лише сила атмосферного тиску:
діє лише сила атмосферного тиску: 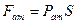 . Шар
. Шар 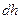 тисне на нижні шари рідини з силою
тисне на нижні шари рідини з силою 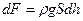 , де
, де 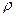 – густина рідини, що аналогічне виникненню додаткової сили тиску:
– густина рідини, що аналогічне виникненню додаткової сили тиску:
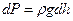 .
.
Нижні шари рідини зазнають додаткового тиску стовпа рідини:
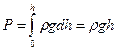 (6.1)
(6.1)
Таким чином, гідростатичний тиск однорідного стовпа рідини висотою 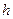 дорівнює:
дорівнює: 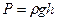 . В тих випадках, коли густина рідини є функцією
. В тих випадках, коли густина рідини є функцією 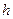 (у першу чергу це стосується газів), в інтегралі у виразі (6.1) замість постійного
(у першу чергу це стосується газів), в інтегралі у виразі (6.1) замість постійного 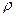 присутня функція
присутня функція 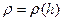 .
.
Іншим важливим законом гідростатики є закон Архімеда: на занурене в рідину (газ)тіло діє виштовхувальна сила, яка чисельно дорівнює вазі витісненої тілом рідини (газу).
Закон Архімеда має важливе значення для вирішення проблем повітроплавання (аеростати, дирижаблі і т. ін.) та проблем, пов’язаних із плаванням, стійкістю та рівновагою надводних та підводних суден.
6.2 Основні поняття гідродинаміки. Стаціонарний рух рідини. Рівняння Бернуллі
Рух рідини (газу) можна вивчати двома методами. Перший метод, запропонований Лагранжем, базується на розгляді рівнянь руху усіх частинок рідини і зводиться до визначення траєкторії, швидкості і прискорення частинки в будь-який момент часу. Використання методу Лагранжа пов’язане із значними математичними труднощами.
На практиці частіше використовують метод Ейлера. У даному розгляді говорять не про швидкість і прискорення окремих частинок рідини, а про швидкість і прискорення потоку рідини у кожній точці простору. Швидкість потоку рідини у даній точці простору залежить від координати точки і часу:
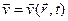
Розглядаємо рух ідеальної рідини, абсолютно нестисливої і повністю позбавленої сил внутрішнього тертя. Для опису властивостей ідеальної рідини користуємося підходом Ейлера. Введемо такі поняття.
1.  Поле вектора швидкості
Поле вектора швидкості 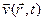 для всіх точок простору, в яких присутня рідина.
для всіх точок простору, в яких присутня рідина.
2. Проведемо в рідині лінії таким чином, щоб дотичні до них у кожній точці співпадали з напрямком 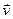 у цій точці (рис. 20). Ці лінії назвемо лініями течії. Густота розміщення ліній течії на рисунку пропорційна величині
у цій точці (рис. 20). Ці лінії назвемо лініями течії. Густота розміщення ліній течії на рисунку пропорційна величині 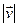 .
.
3. Трубка течії – частина рідини, що обмежена сукупністю ліній течії. Частинки рідини не можуть перетнути стінок трубки течії, бо 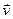 завжди дотичне до ліній течії.
завжди дотичне до ліній течії.
4. Стаціонарне течіння рідини відповідає стану течіння рідини, при якому поле вектора швидкості не залежить від часу: 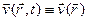 .
.
Важливою характеристикою течіння нестисливої рідини є теорема нерозривності течії. Розглянемо трубку течії (рис.21) у стаціонарному потоці рідини настільки тонку, щоб швидкості рідини можна було вважати сталими у всіх точках будь-якого нормального поперечного перерізу. Обмежимо ділянку трубки течії двома нормальними перерізами 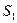 ^
^ 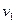 і
і 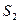 ^
^ 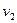
 За час
За час 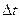 через перерізи перейдуть частинки, що були на відстанях не більших за
через перерізи перейдуть частинки, що були на відстанях не більших за 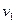
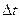 для перерізу
для перерізу 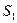 та за
та за 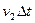 для перерізу
для перерізу 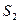 . Для нестисливої рідини кількість частинок, що входять в об’єм, обмежений перерізами
. Для нестисливої рідини кількість частинок, що входять в об’єм, обмежений перерізами 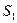 і
і 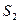 за певний час
за певний час 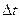 , дорівнює кількості частинок, що виходять з об’єму за цей час. Тому:
, дорівнює кількості частинок, що виходять з об’єму за цей час. Тому:
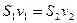 , або
, або 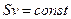 (6.2)
(6.2)
Вираз (6.2) є математичним записом теореми про нерозривність струменя: маса рідини, що проходить за одиницю часу через кожний поперечний переріз трубки течії, для усіх перерізів однакова.
 Опис руху ідеальної рідини у полі сил тяжіння може бути здійснений з допомогою рівняння Бернуллі. Виберемо трубку течії, що перебуває у полі сил тяжіння з певним перепадом висот. Розглянемо переміщення порції рідини, що знаходиться між перерізами
Опис руху ідеальної рідини у полі сил тяжіння може бути здійснений з допомогою рівняння Бернуллі. Виберемо трубку течії, що перебуває у полі сил тяжіння з певним перепадом висот. Розглянемо переміщення порції рідини, що знаходиться між перерізами 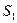 і
і 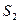 (рис.22).
(рис.22).
За проміжок часу 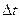 дана порція рідини зміститься у положення між перерізами
дана порція рідини зміститься у положення між перерізами 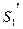 і
і 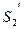 . За теоремою про нерозривність струменя об’єми рідини, що знаходяться між перерізами
. За теоремою про нерозривність струменя об’єми рідини, що знаходяться між перерізами 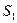 і
і 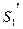 та
та 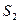 і
і 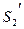 , рівні між собою:
, рівні між собою:
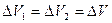
Зміну енергії всієї системи шукаємо як різницю енергій рідини, що перебуває в об’ємах 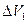 та
та 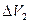 . Нехай густина рідини дорівнює
. Нехай густина рідини дорівнює 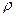 . Вважаємо, що переміщення рідини малі, а тому на проміжках
. Вважаємо, що переміщення рідини малі, а тому на проміжках 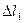 і
і 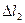 швидкості
швидкості 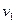 і
і 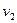 , а також зовнішні тиски
, а також зовнішні тиски 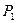 і
і 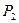 можуть вважатися постійними.
можуть вважатися постійними.
Зміна енергії порції рідини чисельно дорівнює роботі сил тиску 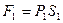 та
та 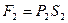 . Ця робота дорівнює:
. Ця робота дорівнює:
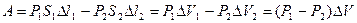
Зміна енергії порції рідини складається із зміни кінетичної та зміни потенціальної енергії:
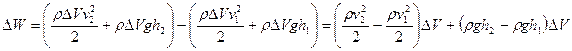 .
.
Прирівняємо 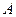 та
та 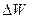 і отримаємо:
і отримаємо:
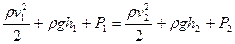 ,
,
або в загальному вигляді для довільної висоти 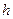 :
:
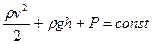 (6.3)
(6.3)
Вираз (6.3) називають рівнянням Бернуллі. У цьому виразі 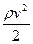 – динамічний тиск, що чисельно дорівнює кінетичній енергії одиниці об’єму рідини,
– динамічний тиск, що чисельно дорівнює кінетичній енергії одиниці об’єму рідини, 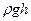 – гідравлічний тиск (тиск стовпа однорідної рідини висотою
– гідравлічний тиск (тиск стовпа однорідної рідини висотою 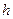 під дією сили тяжіння),
під дією сили тяжіння), 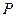 – статичний тиск, обумовлений дією зовнішніх сил.
– статичний тиск, обумовлений дією зовнішніх сил.
Для горизонтальної течії рідини рівняння Бернуллі набуває вигляду:
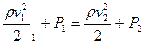 (6.4)
(6.4)
 |
З виразу (6.4) випливає, що у місцях, де швидкість
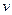 течії більша, тиск
течії більша, тиск 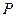 менший. Залежність тиску у рідині від її швидкості лежить в основі дії багатьох пристроїв. Це явище використовується у пульверизаторах, карбюраторах та водоструминних насосах. На рис. 23 показано схему найпростішого водоструминного насоса. Воду з водогону подають через трубку, що має звуження (сопло), з якого вода витікає з великою швидкістю. Це призводить до зниження статичного тиску у даному місці і в результаті з відкачуваної посудини засмоктується повітря. Насос дозволяє отримувати тиски газів майже у 100 разів менші за атмосферний (принципово мінімальний тиск не може бути нижчим за тиск насиченої пари води при даній температурі).
менший. Залежність тиску у рідині від її швидкості лежить в основі дії багатьох пристроїв. Це явище використовується у пульверизаторах, карбюраторах та водоструминних насосах. На рис. 23 показано схему найпростішого водоструминного насоса. Воду з водогону подають через трубку, що має звуження (сопло), з якого вода витікає з великою швидкістю. Це призводить до зниження статичного тиску у даному місці і в результаті з відкачуваної посудини засмоктується повітря. Насос дозволяє отримувати тиски газів майже у 100 разів менші за атмосферний (принципово мінімальний тиск не може бути нижчим за тиск насиченої пари води при даній температурі).
 |
Для експериментального вимірювання тиску в рідині та швидкості потоку рідини використовують прості пристрої у вигляді зігнутих манометричних трубок, поміщених у потік рідини. Найпростішими із них є зонд та трубка Піто (рис. 24).
Трубка Піто (рис.24а) є зігнутою манометричною трубкою з відкритим кінцем, що повернутий назустріч течії рідини. З допомогою трубки Піто вимірюють повний тиск рідини у горизонтальній трубі: 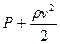 . Статичний тиск
. Статичний тиск 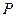 вимірюють з допомогою зонда (рис. 24б). Зонд являє собою зігнуту трубку, запаяну в частині, повернутій назустріч потоку, і з малим отвором у бічній стінці.
вимірюють з допомогою зонда (рис. 24б). Зонд являє собою зігнуту трубку, запаяну в частині, повернутій назустріч потоку, і з малим отвором у бічній стінці.
 Для вимірювання динамічного тиску
Для вимірювання динамічного тиску 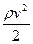 (а таким чином – швидкості рідини) використовують манометричну трубку Прандтля (рис. 24в), що є комбінацією трубки Піто і зонда. З різниці рівнів стовпів рідини
(а таким чином – швидкості рідини) використовують манометричну трубку Прандтля (рис. 24в), що є комбінацією трубки Піто і зонда. З різниці рівнів стовпів рідини 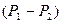 у цих трубках знаходимо
у цих трубках знаходимо 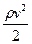 і кінцево розраховуємо швидкість рідини:
і кінцево розраховуємо швидкість рідини:
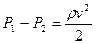
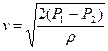 (6.5)
(6.5)
Цікавою для практики є задача про витікання рідини через малий отвір у бічній стінці широкої посудини (рис. 25).
Нехай висота стовпа рідини до центра отвору 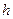 . На вільну поверхню рідини і на струмінь, що витікає діє зовнішній статичний тиск
. На вільну поверхню рідини і на струмінь, що витікає діє зовнішній статичний тиск 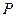 рівний атмосферному. Запишемо рівняння Бернуллі:
рівний атмосферному. Запишемо рівняння Бернуллі:
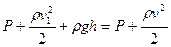 .
.
Оскільки поперечний переріз трубки набагато більший за площу отвору 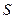 ,
, 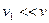 , а тому вважаємо
, а тому вважаємо 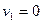 . Тому
. Тому
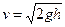 (6.6)
(6.6)
Вираз (6.6) називають формулою Торрічеллі. Об’єм рідини, що витікає через отвір за одиницю часу: 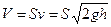 . За час
. За час 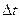 через отвір витікає рідина масою
через отвір витікає рідина масою 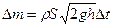 . Ця рідина має швидкість
. Ця рідина має швидкість 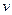 , а тому її імпульс
, а тому її імпульс 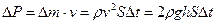 . Згідно з третім законом Ньютона посуд з рідиною отримує від рідини, що витікає імпульс -
. Згідно з третім законом Ньютона посуд з рідиною отримує від рідини, що витікає імпульс - 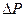 , а тому на посуд діє сила реакції рідини:
, а тому на посуд діє сила реакції рідини:
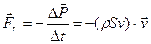 (6.7)
(6.7)
або
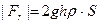 (6.7а)
(6.7а)
Реакція потоку рідини на стінки зігнутої труби. Нехай у зігнутий під деяким кутом трубі постійного перерізу 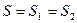 встановився стаціонарний потік рідини (див. рис. 26). За теоремою про нерозривність струменя швидкість протікання рідини
встановився стаціонарний потік рідини (див. рис. 26). За теоремою про нерозривність струменя швидкість протікання рідини 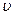 буде однакова за величиною в кожному перерізі.
буде однакова за величиною в кожному перерізі.
 Розглянемо об’єм труби обмежений перерізами
Розглянемо об’єм труби обмежений перерізами 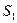 і
і 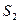 . Через переріз
. Через переріз 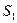 за одиницю часу в об’єм вливається кількість рідини
за одиницю часу в об’єм вливається кількість рідини 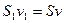 яка вносить в об’єм імпульс
яка вносить в об’єм імпульс 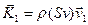 . За одиницю часу з об’єму витікає кількість рідини
. За одиницю часу з об’єму витікає кількість рідини 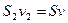 , що виносить з об’єму імпульс
, що виносить з об’єму імпульс 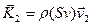 . Таким чином, стінки трубки надають рідині за одиницю часу приріст імпульсу
. Таким чином, стінки трубки надають рідині за одиницю часу приріст імпульсу 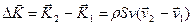 .
.
Згідно з другим законом Ньютона приріст імпульсу тіла за одиницю часу чисельно рівний силі, що діє на тіло. Таким чином зігнута трубка діє на струмінь рідини з силою 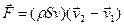 .
.
Згідно з третім законом Ньютона рідина діє на стінки трубки з силою, яка за величиною дорівнює 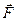 , але протилежна їй за напрямком. Тому сила реакції струменя на стінки труби рівна:
, але протилежна їй за напрямком. Тому сила реакції струменя на стінки труби рівна:
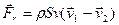 (6.8)
(6.8)
6.3 Рух в’язкої рідини. Ламінарна і турбулентна течія. Формула Пуазейля
У реальній рідині при русі одних шарів відносно інших існують сили в’язкого тертя. Експериментально встановлено, що сили внутрішнього тертя між двома шарами рідини, що рухаються з різними швидкостями 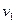 і
і 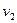 , можна описати з допомогою формули:
, можна описати з допомогою формули:
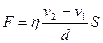 , (6.9)
, (6.9)
У виразі (6.9) 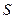 – площа шарів, що взаємодіють,
– площа шарів, що взаємодіють, 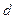 – відстань між шарами,
– відстань між шарами, 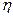 – динамічна в’язкість рідини (коефіцієнт пропорційності, залежний від сорту рідини, її стану, зокрема температури). Більш точно дана залежність описується формулою Ньютона:
– динамічна в’язкість рідини (коефіцієнт пропорційності, залежний від сорту рідини, її стану, зокрема температури). Більш точно дана залежність описується формулою Ньютона:
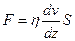 , (6.10)
, (6.10)
тут 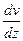 – градієнт швидкості (фактично модуль градієнта швидкості), що має сенс зміни величини
– градієнт швидкості (фактично модуль градієнта швидкості), що має сенс зміни величини 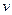 на одиницю відстані у напрямку, перпендикулярному до
на одиницю відстані у напрямку, перпендикулярному до 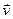 . В’язкість рідини чисельно дорівнює силі тертя між двома шарами площею
. В’язкість рідини чисельно дорівнює силі тертя між двома шарами площею 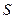 =1 при одиничному градієнті швидкості
=1 при одиничному градієнті швидкості 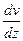 =1. Розмірність в’язкості
=1. Розмірність в’язкості 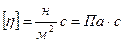 .
.
У багатьох задачах використовують величину 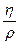 – коефіцієнт кінематичної в’язкості (
– коефіцієнт кінематичної в’язкості ( 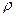 – густина рідини).
– густина рідини).
При розгляді руху рідини розрізняють два крайні типи течії рідини – ламінарну та турбулентну течії.
При ламінарній течії окремі шари рідини не змішуються між собою, ковзаючи один відносно одного. Ламінарна течія є стаціонарною.
Із збільшенням швидкості течії рідини ламінарна течія стає нестійкою і переходить у турбулентну. При турбулентному потоці частинки рідини рухаються по складних траєкторіях, при цьому утворюються вихори із замкненими траєкторіями, рідина інтенсивно перемішується.
Умови переходу від ламінарної до турбулентної течії характеризуються числом Рейнольдса:
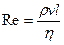 , (6.11)
, (6.11)
у якому 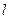 – характерний розмір тіла, що взаємодіє з рідиною. Для передбачення характеру руху рідини в конкретних задачах використовують розрахунок числа Рейнольдса. При малих величинах
– характерний розмір тіла, що взаємодіє з рідиною. Для передбачення характеру руху рідини в конкретних задачах використовують розрахунок числа Рейнольдса. При малих величинах 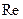 спостерігається ламінарна течія рідини. Починаючи з якогось критичного значення числа Рейнольдса течія рідини набуває турбулентного характеру.
спостерігається ламінарна течія рідини. Починаючи з якогось критичного значення числа Рейнольдса течія рідини набуває турбулентного характеру.
Зокрема, для гладкої циліндричної труби круглого перерізу діаметром 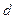 критичне число Рейнольдса дорівнює :
критичне число Рейнольдса дорівнює :
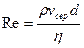 =2300,
=2300,
де 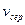 – середня швидкість течії рідини. Для води в трубі діаметром 0,02 м при
– середня швидкість течії рідини. Для води в трубі діаметром 0,02 м при 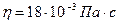 середня швидкість, при якій число Рейнольдса досягає критичного значення, дорівнює 0,2 м/с.
середня швидкість, при якій число Рейнольдса досягає критичного значення, дорівнює 0,2 м/с.
 |
Проаналізуємо більш детально стаціонарну течію рідини в розміщеній горизонтально однорідній циліндричній трубі радіуса
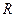 . Знайдемо закон зміни швидкості рідини
. Знайдемо закон зміни швидкості рідини 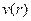 від осі трубки (
від осі трубки ( 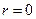 ) до її стінок (
) до її стінок ( 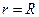 ). Уявно виділимо у рідині циліндричний об’єм радіусом
). Уявно виділимо у рідині циліндричний об’єм радіусом 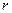 і довжиною
і довжиною 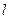 , вісь якого співпадає з віссю трубки (рис. 27).
, вісь якого співпадає з віссю трубки (рис. 27).
При стаціонарному русі рідини сумарна сила тиску 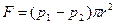 зрівноважується силою тертя
зрівноважується силою тертя 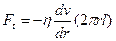 , де
, де 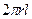 – площа бічної поверхні вибраного циліндра,
– площа бічної поверхні вибраного циліндра, 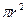 – площа основи циліндра,
– площа основи циліндра, 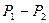 – перепад тиску між основами циліндра,
– перепад тиску між основами циліндра, 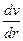 – градієнт швидкості. Запишемо цю умову у вигляді рівняння і знайдемо з нього
– градієнт швидкості. Запишемо цю умову у вигляді рівняння і знайдемо з нього 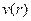 :
:
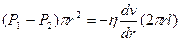 (6.12)
(6.12)
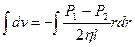
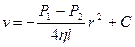
Оскільки швидкість рідини на стінках дорівнює нулю, 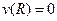 при
при 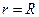 , то
, то
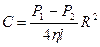
Кінцево:
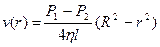 (6.13)
(6.13)
Якщо вважати, що швидкість рідини на осі труби 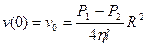 , то вираз (6.13) можна записати:
, то вираз (6.13) можна записати:
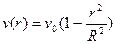 (6.14)
(6.14)
З виразу (6.14) видно, що залежність 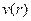 параболічна (рис. 28).
параболічна (рис. 28).
 Вираз (6.13) можна використати для розрахунку об’єму рідини, що протікає через поперечний переріз труби за одиницю часу. Для цього поперечний переріз труби розіб’ємо на концентричні кільця радіуса
Вираз (6.13) можна використати для розрахунку об’єму рідини, що протікає через поперечний переріз труби за одиницю часу. Для цього поперечний переріз труби розіб’ємо на концентричні кільця радіуса 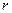
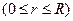 товщиною
товщиною 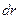 (рис. 29) Площа кільця дорівнює
(рис. 29) Площа кільця дорівнює 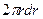 . За одиницю часу через поперечний переріз кільця протікає об’єм рідини
. За одиницю часу через поперечний переріз кільця протікає об’єм рідини 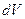 , який дорівнює:
, який дорівнює:
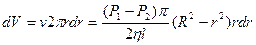 (6.15)
(6.15)
Знаходимо суму об’ємів рідини, яка пройшла за одиницю часу через усі кільця:
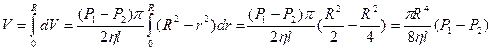 (6.16)
(6.16)
 Вираз (6.16) називають формулою Пуазейля. З допомогою цього виразу знаходимо кількість (об’єм) рідини, що протікає через поперечний переріз круглої труби радіуса
Вираз (6.16) називають формулою Пуазейля. З допомогою цього виразу знаходимо кількість (об’єм) рідини, що протікає через поперечний переріз круглої труби радіуса 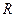 за одиницю часу. З виразу видно, що
за одиницю часу. З виразу видно, що 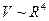 , а тому збільшення радіуса труби у два рази дозволяє збільшити об’єм рідини у 16 разів. Вираз (6.16) справедливий лише для ламінарної течії рідини.
, а тому збільшення радіуса труби у два рази дозволяє збільшити об’єм рідини у 16 разів. Вираз (6.16) справедливий лише для ламінарної течії рідини.
6.4 Рух твердих тіл у рідинах
Будь-яке тіло при русі у нерухомій рідині зазнає дії сил опору середовища. Визначення цих сил шляхом розрахунку являє собою складну математичну задачу. Тому звичайно розв’язують еквівалентну задачу про обтікання твердого тіла потоком рідини.
Силу, що діє на тіло з боку рідини, можна розкласти на дві складові: у напрямку потоку 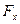 і перпендикулярну до потоку
і перпендикулярну до потоку 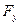 . Силу
. Силу 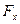 називають силою лобового опору, а силу
називають силою лобового опору, а силу 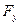 – підіймальною силою. Сила лобового опору
– підіймальною силою. Сила лобового опору 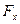 складається з двох різних сил: сили, обумовленої різницею тисків на передню і задню поверхні тіла та сили в’язкого тертя. При великих швидкостях
складається з двох різних сил: сили, обумовленої різницею тисків на передню і задню поверхні тіла та сили в’язкого тертя. При великих швидкостях 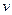 (великих числах Рейнольдса) переважаючу роль відіграють сили, обумовлені різницею тисків, при малих
(великих числах Рейнольдса) переважаючу роль відіграють сили, обумовлені різницею тисків, при малих 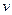 – сили в’язкості.
– сили в’язкості.
При обтіканні твердого тіла стаціонарним потоком ідеальної нев’язкої нестисливої рідини чи при рівномірному русі тіла в такій рідині лобовий опір дорівнює нулю. Ідеальна нев’язка рідина повинна вільно ковзати по поверхні тіла, повністю обтікаючи його. На рис.30 показано лінії течіння при обтіканні ідеальною рідиною довгого циліндра. Внаслідок повного обтікання тіла картина ліній течіння є повністю симетрична відносно прямої, що проходить по діаметру, паралельному вектору 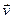 рідини далеко від циліндра. Тиск поблизу точок А і В буде вищим, ніж у незбуреному потоці рідини і рівним у обидвох точках. (Збільшення тиску в точках А і В обумовлене зменшенням швидкості потоку в цих точках у порівнянні із швидкістю незбуреної рідини).
рідини далеко від циліндра. Тиск поблизу точок А і В буде вищим, ніж у незбуреному потоці рідини і рівним у обидвох точках. (Збільшення тиску в точках А і В обумовлене зменшенням швидкості потоку в цих точках у порівнянні із швидкістю незбуреної рідини).
 |
Тому результуюча сила лобового опору в даному випадку відсутня. Цей висновок називають парадоксом Даламбера.
Симетрична картина взаємодії ідеальної рідини з тілом спостерігається і для точок С та Д, розміщених на діаметрі СД, перпендикулярному до АВ.
У випадку взаємного руху тіла і в’язкої рідини дуже тонкий шар рідини примикає до поверхні тіла і рухається з ним як єдине ціле, захоплюючи з собою внаслідок тертя подальші шари рідини. У результаті тіло оточене шаром рідини, в якому існує градієнт швидкості. Цей шар називають суміжним, у ньому діють сили внутрішнього тертя, які спричинюють виникнення сил опору. Із збільшенням швидкості рідини змінюється характер обтікання циліндра рідиною (рис. 31).
 |
Тангенціальні сили внутрішнього тертя, які діють у суміжному шарі, спричинюють обертальний рух частинок рідини і відбувається відривання потоку від поверхні циліндра з утворенням вихорів, а у результаті з виникненням ділянки із зниженим тиском. Тому, як уже відзначалося вище, існують дві причини виникнення сили лобового опору рухові тіла відносно в’язкої рідини:
а) дотичні сили в’язкості (опір внутрішнього тертя), які відіграють основну роль при малих швидкостях. Величина цих сил пропорційна першій степені швидкості:
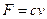 . (6.17)
. (6.17)
 |
тут
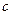 – коефіцієнт пропорційності, залежний від в’язкості рідини, розмірів і форми тіла, його орієнтації відносно потоку рідини.
– коефіцієнт пропорційності, залежний від в’язкості рідини, розмірів і форми тіла, його орієнтації відносно потоку рідини.
б) опір тиску зростає приблизно пропорційно до 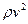 і відіграє переважаючу роль при великих швидкостях:
і відіграє переважаючу роль при великих швидкостях:
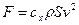 , (6.18)
, (6.18)
де 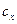 – коефіцієнт пропорційності, залежний від числа Рейнольдса, форми тіла та його орієнтації у потоці рідини,
– коефіцієнт пропорційності, залежний від числа Рейнольдса, форми тіла та його орієнтації у потоці рідини, 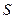 – площа поперечного перерізу тіла.
– площа поперечного перерізу тіла.
При даних поперечних розмірах тіла опір тиску сильно залежить від форми тіла. Співвідношення між силами опору тертя і силами опору тиску визначаються числом Рейнольдса.
Як уже згадувалося, у випадку, коли тіло несиметричне, обтікання тіла ідеальною рідиною веде до появи сили 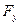 , перпендикулярної до вектора швидкості
, перпендикулярної до вектора швидкості 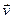 , яку називають підіймальною силою. Для виникнення підіймальної сили в’язкість рідини не має суттєвого значення. На прикладі обтікання ідеальною рідиною напівциліндра (Рис. 32) показано, що підіймальна сила може бути напрямлена як вгору, так і вниз. Виникнення підіймальної сили обумовлене різними швидкостями рідини, а відповідно і різними величинами тиску
, яку називають підіймальною силою. Для виникнення підіймальної сили в’язкість рідини не має суттєвого значення. На прикладі обтікання ідеальною рідиною напівциліндра (Рис. 32) показано, що підіймальна сила може бути напрямлена як вгору, так і вниз. Виникнення підіймальної сили обумовлене різними швидкостями рідини, а відповідно і різними величинами тиску 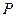 . Підіймальна сила може бути розрахована з допомогою виразу :
. Підіймальна сила може бути розрахована з допомогою виразу :
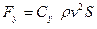 , (6.19)
, (6.19)
тут 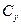 – коефіцієнт пропорційності, залежний від числа Рейнольдса, форми тіла і його орієнтації у потоці рідини,
– коефіцієнт пропорційності, залежний від числа Рейнольдса, форми тіла і його орієнтації у потоці рідини,  – площа поперечного перерізу тіла.
– площа поперечного перерізу тіла.
Завдяки підіймальній силі можливий рух корабля на підводних крилах, політ літака у повітрі і ін. Крило літака має обтічну форму профілю, подібному (рис. 32а). Орієнтація крила літака відносно потоку повітря здійснюється таким чином, щоб вибрати оптимальне його положення, при якому забезпечується достатня підіймальна сила з обмеженою величиною лобового опору.
Одним з явищ, яке спостерігається при взаємному русі тіла і рідини, є ефект Магнуса, що проявляється при обертовому русі тіла у потоці рідини . Причину виникнення даного ефекту можна вияснити на основі такого експерименту. Нехай зображений на рис. 33 циліндр обертається у напрямку руху годинникової стрілки. У цьому випадку в точці А поблизу циліндра його обертання сприяє прискоренню руху рідини у напрямку течії, а у точці В обертання циліндра сповільнює рух рідини. У результаті на циліндр діє підіймальна сила, зумовлена різницею тисків рідини між точками А і В.
Прояв впливу ефекту Магнуса на рух тіла можна продемонструвати при розгляді руху легкого порожнистого циліндра, що скочується по похилій площині (рис. 34).
Ефектом Магнуса пояснюються непрямолінійні траєкторії руху тенісного чи футбольного м’яча після здійснення „різаних” ударів. Впливом ефекту Магнуса пояснюється і невелика точність стрільби кулястими снарядами (дріб, ядра) гармат та мисливських рушниць, у яких відсутня нарізка у стволі.
 |
 |
Дата добавления: 2015-09-11; просмотров: 2510;
