Основи динаміки
2.1 Закони динаміки матеріальної точки
Видатний італійський учений Галілео Галілей показав, що всяке тіло має властивість зберігати швидкість свого руху, а змінити цей стан може лише дія інших тіл. Властивість тіла зберігати стан спокою або рівномірного прямолінійного руху називають інертністю тіла. Мірою інертності тіла є його маса 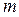 . На основі даного факту Ісааком Ньютоном було сформульовано три основні закони динаміки, які в сучасному трактуванні виглядають так:
. На основі даного факту Ісааком Ньютоном було сформульовано три основні закони динаміки, які в сучасному трактуванні виглядають так:
1. Існують системи відліку, відносно яких тіло перебуває в стані спокою або рівномірного прямолінійного руху, якщо дія на нього інших тіл відсутня або компенсується.
Системи відліку, для яких виконується перший закон Ньютона, називають інерційними. Поняття інерційної системи дещо неозначене, оскільки одна і та ж система відліку, в залежності від характеру задачі, може бути інерційною або неінерційною. Стверджуємо, що інерційною є система відліку, яка рухається рівномірно і прямолінійно (або перебуває в стані спокою) відносно іншої інерційної системи відліку. Закони Ньютона виконуються лише в інерційних системах відліку.
Оскільки зміна стану руху тіла визначається дією на тіло інших тіл, то кількісно цю дію характеризуємо векторною величиною 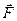 – силою. З результатів експериментів випливає другий закон динаміки Ньютона.
– силою. З результатів експериментів випливає другий закон динаміки Ньютона.
2. Прискорення, з яким рухається тіло, прямо пропорційне силі 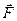 , що діє на тіло і обернено пропорційне масі тіла:
, що діє на тіло і обернено пропорційне масі тіла:
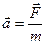 , або
, або 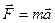 (2.1)
(2.1)
У даному виразі 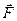 - сумарна сила, що діє на тіло з боку
- сумарна сила, що діє на тіло з боку 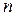 інших тіл (
інших тіл ( 
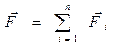 ). Відзначимо, що поняття маси
). Відзначимо, що поняття маси 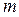 може бути введене як з другого закону Ньютона (
може бути введене як з другого закону Ньютона ( 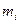 - інертна маса), так із закону всесвітнього тяжіння
- інертна маса), так із закону всесвітнього тяжіння
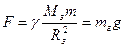 , (2.2)
, (2.2)
( 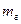 - гравітаційна маса тіла,
- гравітаційна маса тіла, 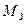 – маса Землі). Досліди показують, що дані маси принаймні прямо пропорційні. Тому надалі вважатимемо
– маса Землі). Досліди показують, що дані маси принаймні прямо пропорційні. Тому надалі вважатимемо 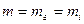 . .Принцип тотожності гравітаційної та інертної мас покладено в основу загальної теорії відносності.
. .Принцип тотожності гравітаційної та інертної мас покладено в основу загальної теорії відносності.
3. Дія одного тіла на інше має характер взаємодії: тіла взаємодіють з силами рівними за величиною та протилежними за напрямком
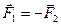 (2.3)
(2.3)
За характером взаємодії в механіці розрізняють три типи сил: сили тяжіння, сили тертя і пружні сили. Сили тяжіння проявляють себе як результат взаємодії тіл на відстані через гравітаційне поле. Сили тертя та пружні сили за своєю природою електромагнітні і проявляються в результаті взаємодії тіл через дотик.
Вираз другого закону Ньютона можна подати в наступному вигляді:
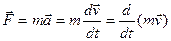 , або
, або 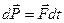 . (2.4)
. (2.4)
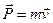 - імпульс тіла,
- імпульс тіла, 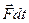 - імпульс сили. З останнього виразу випливає, що необхідною умовою збереження імпульсу тіла
- імпульс сили. З останнього виразу випливає, що необхідною умовою збереження імпульсу тіла 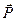 є
є 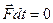 . Тобто імпульс тіла залишається сталим, якщо імпульс прикладених до тіла сил дорівнює нулеві.
. Тобто імпульс тіла залишається сталим, якщо імпульс прикладених до тіла сил дорівнює нулеві.
Важливим наслідком другого закону Ньютона є можливість повністю описати рух тіла, якщо відомі аналітичні вирази для залежностей діючих сил від координат і часу, а також задано початкові положення і швидкість тіла. В цьому випадку рівняння , що виражає другий закон Ньютона, перетворюється в так зване рівняння руху. Зокрема, для руху матеріальної точки отримуємо:
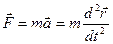 , або
, або 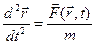 . (2.5)
. (2.5)
В останньому виразі 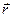 - радіус вектор (координата) матеріальної точки.
- радіус вектор (координата) матеріальної точки.
2.2 Закони динаміки системи матеріальних точок. Теорема про рух центра мас
Розглянемо систему, що складається з 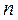 - матеріальних точок (
- матеріальних точок ( 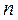 - скінченне число). Рух такої системи зручно описувати, ввівши поняття центра мас системи. Нехай маса
- скінченне число). Рух такої системи зручно описувати, ввівши поняття центра мас системи. Нехай маса 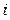 - тої точки
- тої точки 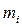 , а її координата
, а її координата 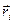 . Центром мас системи вважаємо точку, координата якої може бути визначена із співвідношення
. Центром мас системи вважаємо точку, координата якої може бути визначена із співвідношення
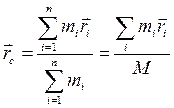 , (2.6)
, (2.6)
або
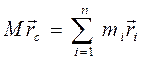 ,
,
де 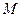 - сумарна маса системи матеріальних точок.
- сумарна маса системи матеріальних точок.
Встановимо закон руху центра мас. Для цього використаємо закономірності руху кожної з точок системи. Оскільки 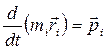 - імпульс
- імпульс 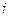 -тої точки, то сумарний імпульс системи:
-тої точки, то сумарний імпульс системи:
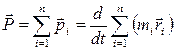 . (2.7)
. (2.7)
З рівняння руху довільної матеріальної точки:
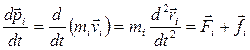 , (2.8)
, (2.8)
де 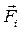 - зовнішня сила, що діє на матеріальну точку, а
- зовнішня сила, що діє на матеріальну точку, а 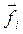 - сума внутрішніх сил, які діють на
- сума внутрішніх сил, які діють на 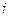 - ту матеріальну точку з боку інших точок системи:
- ту матеріальну точку з боку інших точок системи: 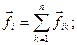 (
( 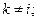
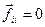 , оскільки і-та матеріальна точка сама з собою не взаємодіє). Таким чином рівняння руху системи матеріальних точок може бути записане у вигляді:
, оскільки і-та матеріальна точка сама з собою не взаємодіє). Таким чином рівняння руху системи матеріальних точок може бути записане у вигляді:
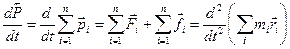 .
.
Згідно з третім законом Ньютона 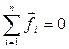 , тому
, тому
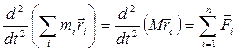 ( 2.9)
( 2.9)
З останнього виразу випливає, що центр мас системи матеріальних точок рухається так, як рухалося б тіло масою 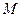 під дією всіх прикладених зовнішніх сил.
під дією всіх прикладених зовнішніх сил.
2.3 Закон динаміки обертального руху матеріальної точки
Розглянемо обертальний рух матеріальної точки масою 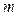 відносно точки О під дією сили
відносно точки О під дією сили 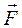 , яка в даний момент часу лежить в площині руху
, яка в даний момент часу лежить в площині руху
 (рис.2). Складова сили
(рис.2). Складова сили 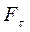 надає матеріальній точці тангенціального прискорення, модуль якого
надає матеріальній точці тангенціального прискорення, модуль якого 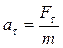 .
.
Тоді 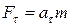 .
.
Дія нормальної складової сили 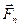 зводиться лише до надання точці
зводиться лише до надання точці 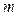 нормального прискорення (закручування траєкторії). Оскільки за даних умов
нормального прискорення (закручування траєкторії). Оскільки за даних умов 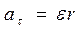 , то:
, то:
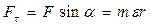
Домножимо вираз на 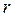 :
:
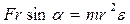 .
.
Ввівши позначення 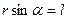 ,
, 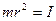 ,
, 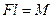 , запишемо останній вираз у вигляді:
, запишемо останній вираз у вигляді:
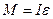 , (2.10 )
, (2.10 )
де 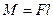 – момент сили
– момент сили 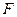 відносно точки О, l – плече сили,
відносно точки О, l – плече сили, 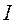 - момент інерції матеріальної точки
- момент інерції матеріальної точки 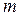 відносно точки О.
відносно точки О.
Вираз (2.10 ) за своїм виглядом є аналогом другого закону Ньютона для криволінійного руху з тією різницею, що аналогом сили 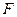 є момент сили
є момент сили 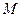 , маси
, маси 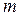 – момент інерції
– момент інерції 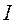 , прискорення
, прискорення 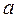 – кутове прискорення
– кутове прискорення 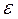 .
.
Оскільки точка рухається по колу сталого радіуса (r = const), то її момент інерції 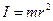 також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:
також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:
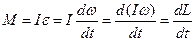 .
.
У векторному записі (рис.3)
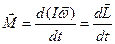 . (2.11)
. (2.11)
Вектор 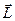 називають моментом імпульсу матеріальної точки відносно точки О. Даний вектор, який в умовах даної задачі чисельно дорівнює
називають моментом імпульсу матеріальної точки відносно точки О. Даний вектор, який в умовах даної задачі чисельно дорівнює 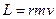 , є аналогом вектора імпульсу
, є аналогом вектора імпульсу 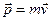 для прямолінійного руху.
для прямолінійного руху.
Розглянемо загальний випадок, коли сила 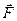 не лежить в одній площині з існуючою коловою траекторією. За другим законом Ньютона рівняння руху матеріальної точки маси
не лежить в одній площині з існуючою коловою траекторією. За другим законом Ньютона рівняння руху матеріальної точки маси 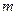 має вигляд:
має вигляд:
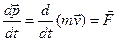 .
.
 Домножимо даний вираз векторно на
Домножимо даний вираз векторно на 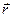 . Тут
. Тут 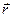 – радіус-вектор матеріальної точки масою m, проведений з деякої нерухомої точки О (центра обертання) до точки
– радіус-вектор матеріальної точки масою m, проведений з деякої нерухомої точки О (центра обертання) до точки 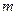 . Зауважимо, що
. Зауважимо, що 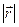 = const, оскільки розглядаємо лише обертовий рух. Тоді
= const, оскільки розглядаємо лише обертовий рух. Тоді
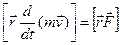
Ліву частину останнього виразу запишемо у вигляді:
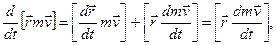 (2.12)
(2.12)
оскільки 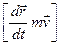 =
= 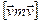 =0.
=0.
Вектор 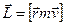 назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор
назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор 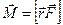 – моментом сили
– моментом сили 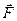 відносно точки О. Ввівши згадані позначення у вираз (2.12), отримаємо
відносно точки О. Ввівши згадані позначення у вираз (2.12), отримаємо
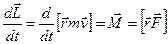 (2.13)
(2.13)
Вираз 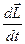 =
= 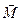 називають рівнянням моментів.
називають рівнянням моментів.
Після перетворення вираз (2.13) кінцево можна записати у вигляді, подібному до (2.10):
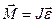 , (2.14)
, (2.14)
оскільки 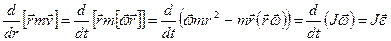 , а
, а  =0, бо
=0, бо  .
.
В останньому перетворенні використана відома формула для подвійного векторного добутку.
Якщо через точку О провести довільну вісь z , то проекції векторів 
і  на цю вісь
на цю вісь 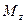 і
і 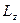 називають відповідно моментом сили
називають відповідно моментом сили 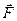 відносно осі z та моментом імпульсу матеріальної точки відносно осі
відносно осі z та моментом імпульсу матеріальної точки відносно осі 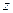 (рис.4 і рис.5).
(рис.4 і рис.5).
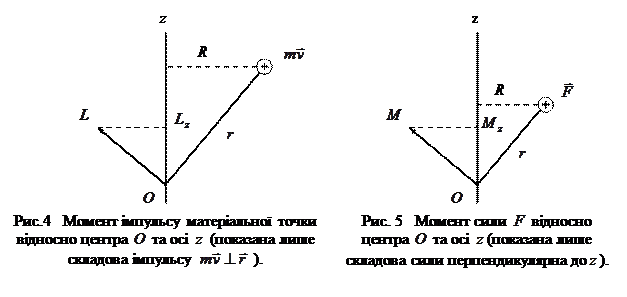
2.4 Закон динаміки обертального руху абсолютно твердого тіла
Усяке тверде тіло можна умовно розбити на деяку кількість n настільки малих частин, що розмірами кожної частини в порівнянні з розмірами твердого тіла можна нехтувати. Це дозволяє розглядати тверде тіло як сукупність скінченого числа n матеріальних точок. Маса тіла 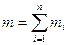 , де
, де 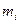 – маса і – тої матеріальної точки, причому і = 1, 2, 3, ..., n. Розглянемо закономірності руху тіла, закріпленого в нерухомій точці О, яка поміщена в початку інерційної системи відліку. У цьому випадку точка О є центром обертання. Положення кожної і – тої матеріальної точки визначається її радіус-вектором
– маса і – тої матеріальної точки, причому і = 1, 2, 3, ..., n. Розглянемо закономірності руху тіла, закріпленого в нерухомій точці О, яка поміщена в початку інерційної системи відліку. У цьому випадку точка О є центром обертання. Положення кожної і – тої матеріальної точки визначається її радіус-вектором 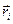 , проведеним від центра обертання О до даної точки.
, проведеним від центра обертання О до даної точки.
Рівняння руху довільної матеріальної точки тіла можна бути записати згідно (2.8)
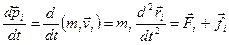 , (2.15)
, (2.15)
де 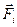 - сумарна зовнішня сила, що діє на
- сумарна зовнішня сила, що діє на 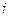 -ту матеріальну точку, а
-ту матеріальну точку, а 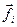 - сума внутрішніх сил, що діють на точку
- сума внутрішніх сил, що діють на точку 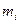 з боку інших частинок тіла:
з боку інших частинок тіла: 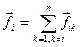 .
.
Помножимо вираз (2.15) векторно на 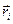 :
:
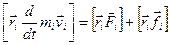
Врахувавши особливості виведення виразу (2.13) для однієї точки, отримаємо:
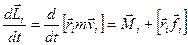 , (2.16)
, (2.16)
де 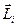 – момент імпульсу i-тої матеріальної точки,
– момент імпульсу i-тої матеріальної точки, 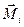 – сумарний момент зовнішніх сил,
– сумарний момент зовнішніх сил, 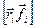 – сумарний момент внутрішніх сил, що діють на дану точку.
– сумарний момент внутрішніх сил, що діють на дану точку.
Просумувавши вирази, записані для кожної точки, отримаємо для тіла в цілому
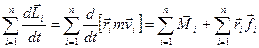 . (2.17)
. (2.17)
Введемо позначення 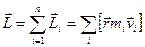 –момент імпульсу тіла відносно точки О,
–момент імпульсу тіла відносно точки О, 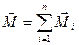 – результуючий (головний) момент зовнішніх сил, що діють на тіло, відносно точки О, і врахуємо[1], що
– результуючий (головний) момент зовнішніх сил, що діють на тіло, відносно точки О, і врахуємо[1], що 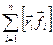 =0.
=0.
Кінцево отримаємо:
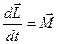 (2.18)
(2.18)
Коли тіло закріплене у двох нерухомих точках О і О', то воно може обертатися відносно нерухомої осі z , що проходить через ці точки. Обертання відносно даної осі відбувається під дією складової 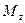 моменту зовнішніх сил
моменту зовнішніх сил 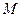 . За цих умов рівняння (2.18) зведеться до вигляду:
. За цих умов рівняння (2.18) зведеться до вигляду:
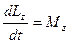 (2.19)
(2.19)
Проекції L i M на вісь обертання називаються моментом імпульсу тіла 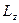 та результуючим моментом зовнішніх сил відносно осі обертання z .
та результуючим моментом зовнішніх сил відносно осі обертання z .
Знайдемо вираз для розрахунку моменту імпульсу тіла 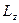 відносно заданої осі обертання
відносно заданої осі обертання 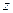 :
:
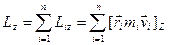 .
.
Обертання відбувається навколо нерухомої осі, жорстко пов’язаної з тілом, і всі частини тіла здійснюють плоскі рухи в площинах, перпендикулярних до осі z . За цих умов потрібно враховувати складові 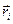 та
та 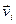 , що перпендикулярні до осі z . Тому
, що перпендикулярні до осі z . Тому
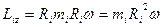 , (2.20)
, (2.20)
де 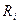 – відстань
– відстань 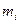 від осі обертання, а
від осі обертання, а 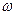 – кутова швидкість обертання.
– кутова швидкість обертання.
Таким чином,
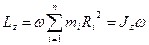 ,
,
де 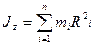 – момент інерції абсолютно твердого тіла відносно осі z . В інтегральній формі, коли тіло розглядають як сукупність нескінченно малих елементів маси
– момент інерції абсолютно твердого тіла відносно осі z . В інтегральній формі, коли тіло розглядають як сукупність нескінченно малих елементів маси 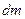 , вираз для
, вираз для 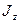 запишемо у вигляді:
запишемо у вигляді:
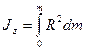 , (2.21)
, (2.21)
де R – відстань елементарної маси 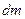 від осі обертання.
від осі обертання.
З наведених вище виразів випливає, що момент інерції тіла залежить від його маси, геометрії тіла та положення осі обертання відносно тіла. Зокрема, моменти інерції однорідних тіл правильної геометричної форми можна обчислити за допомогою наступних виразів:
1. Порожнистий тонкостінний циліндр маси m та радіуса R відносно геометричної осі симетрії , що проходить через центр маси:
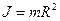
2. Порожнистий товстостінний циліндр масою m та радіусами циліндричних поверхонь 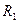 і
і 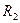 відносно геометричної осі симетрії , що проходить через центр маси:
відносно геометричної осі симетрії , що проходить через центр маси:
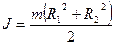
3. Суцільний циліндр (диск) масою m та радіусом R відносно геометричної осі симетрії , що проходить через центр маси:
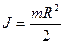
4. Куля масою m та радіусом R відносно осі, що проходить через центр мас кулі:
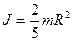 .
.
5. Однорідний тонкий стрижень маси m, довжини l відносно осі, що перпендикулярна до стрижня і проходить через його центр мас:
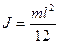
6. Однорідний стрижень маси m і довжини l відносно осі, що перпендикулярна до стрижня і проходить через його кінець:
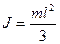
Якщо вісь обертання зміщена відносно центра мас тіла, то для розрахунку моменту інерції тіла користуються виразом, отриманим на основі теореми Гюйгенса – Штайнера: момент інерції тіла 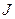 відносно довільної осі дорівнює сумі моменту інерції
відносно довільної осі дорівнює сумі моменту інерції 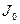 відносно осі, яка проходить через центр мас тіла і паралельна заданій , і добутку маси тіла на квадрат відстані a між осями:
відносно осі, яка проходить через центр мас тіла і паралельна заданій , і добутку маси тіла на квадрат відстані a між осями:
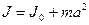 (2.22)
(2.22)
Прикладом, що ілюструє правильність теореми Гюйгенса – Штайнера, є результат розрахунку моменту інерції однорідного стрижня довжини l та маси m відносно осі, що проходить через центр мас перпендикулярно до стрижня 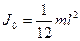 та відносно осі, що проходить через його кінець перпендикулярно до стрижня
та відносно осі, що проходить через його кінець перпендикулярно до стрижня 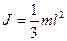 :
:
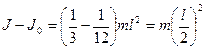
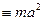 .
.
3 Сили в механіці
Сила характеризує взаємодію тіл. Дія сили може призвести до зміни особливостей руху тіла або до деформації тіл. У природі всі сили можна поділити на дві категорії:
1. Сили, зумовлені взаємодією тіл при їх безпосередньому дотику (удар, тиск, тяга, тертя і т. ін.).
2. Сили, обумовлені взаємодією тіл через силове поле.
Під силовим полем розуміємо певний напружений стан простору, який виникає навколо джерела поля і проявляється в тому, що на внесені в це поле тіла діють певні сили.
На даний час фізика визнає існування чотирьох основних типів фундаментальних взаємодій, проявом яких і є всі відомі силові взаємодії, що описують фізичні явища. Фундаментальними є гравітаційні, електромагнітні, сильні і слабкі взаємодії. Гравітаційні та електромагнітні взаємодії пояснюють всі відомі явища в макросвіті.
Зокрема, дією гравітаційних сил пояснюють стабільність астрономічних об’єктів (зірок, планет, комет і ін), утримання макроскопічних тіл на поверхні планет. Гравітаційні поля впливають на закономірності взаємних переміщень астрономічних об’єктів (рух планет у полях зірок, рух супутників і т. ін.).
Електромагнітні взаємодії відповідальні за існування і стійкість атомів та молекул, за перебіг хімічних реакцій, за зміну агрегатного стану речовини, за виникнення пружних сил і сил тертя.
Сильні (ядерні) та слабкі взаємодії проявляються на дуже малих відстанях між об’єктами (r < 10-15 м) і відіграють основну роль в поясненні явищ мікросвіту. Зокрема, дією ядерних сил обумовлені існування атомних ядер та їх стійкість. Сили слабкої взаємодії проявляються при 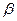 – розпаді атомних ядер та при взаємодії нейтрино з речовиною.
– розпаді атомних ядер та при взаємодії нейтрино з речовиною.
В класичній механіці при розгляді руху та взаємодії макроскопічних тіл звичайно зустрічаються з дією гравітаційних сил та сил тертя і пружності, які за своєю природою є електромагнітними.
3.1 Гравітаційні сили.
Закон всесвітнього тяжіння був установлений Ісааком Ньютоном на основі емпіричних законів Кеплера, що описують рух планет навколо Сонця. Згідно з цим законом між усякими двома матеріальними точками діють сили взаємного притягання, величина яких прямо пропорційна добутку мас точок 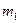 і
і 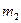 та обернено пропорційна квадрату відстані r між ними:
та обернено пропорційна квадрату відстані r між ними:
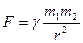 (3.1)
(3.1)
Коефіцієнт пропорційності 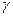 – гравітаційна стала, фізичний сенс якої наступний: вона чисельно дорівнює силі взаємного притягання двох точок одиничної маси, що перебувають на відстані, яка дорівнює одиниці довжини.
– гравітаційна стала, фізичний сенс якої наступний: вона чисельно дорівнює силі взаємного притягання двох точок одиничної маси, що перебувають на відстані, яка дорівнює одиниці довжини.
Для макроскопічних тіл сила взаємного притягання визначається як сума сил попарних взаємодій складових частинок обох тіл. У випадку взаємодії тіл кулеподібної форми вираз для сумарної сили притягання аналогічний до (3.1), причому маси 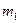 і
і 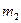 – маси тіл, а
– маси тіл, а 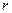 – відстань між їхніми центрами. Аналогічний результат отримується, коли тіло більшої маси має кулясту форму, а інше тіло має набагато меншу масу і розміри. Зокрема така ситуація реалізується для тіл, що перебувають на поверхні Землі:
– відстань між їхніми центрами. Аналогічний результат отримується, коли тіло більшої маси має кулясту форму, а інше тіло має набагато меншу масу і розміри. Зокрема така ситуація реалізується для тіл, що перебувають на поверхні Землі:
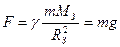 (3.2)
(3.2)
Вираз (3.2) справедливий і для тіл, що містяться над поверхнею Землі на висоті 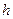 , бо зміна прискорення земного тяжіння
, бо зміна прискорення земного тяжіння 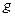 незначна при умові, що
незначна при умові, що 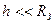 :
:
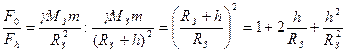 (3.3)
(3.3)
Простий розрахунок показує, що при 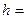 1 км g змінюється лише на 0,03%.
1 км g змінюється лише на 0,03%.
Оскільки реальна форма Землі відмінна від сферичної, а також внаслідок добового обертання величина 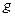 залежить від географічної широти точки обертання, змінюючись від 9,83 м/с2 на полюсах до 9,78 м/с2 на екваторі.
залежить від географічної широти точки обертання, змінюючись від 9,83 м/с2 на полюсах до 9,78 м/с2 на екваторі.
Гравітаційна взаємодія між тілами на відстані здійснюється за допомогою поля тяжіння (гравітаційного поля). Кожне тіло є джерелом гравітаційного поля, тобто такого збурення властивостей навколишнього середовища, яке проявляється в тому, що на внесене у будь яку точку поля інше тіло діє сила тяжіння, характерна для даної точки поля. У полі сил тяжіння має місце принципсуперпозиції: за наявності декількох джерел полів сумарна гравітаційна сила, що діє на деяке тіло дорівнює векторній сумі сил, які діють на нього з боку кожного з джерел поля.
3.2 Сили тертя
На механічний рух у середовищі завжди впливають сили тертя і опору, які протидіють взаємному переміщенню тіл чи їхніх частин.
Сили тертя, що виникають у процесі відносного руху тіл або їх частинок по поверхні інших тіл називають силами зовнішнього або сухого тертя.
Сили тертя, що виникають при відносному русі між твердим тілом і рідиною (газом) або між шарами рідин чи газів називають силами внутрішнього (в’язкого) тертя.
Розрізняють два види сил сухого тертя:
1. Тертя спокою (статичне тертя) існує між взаємно нерухомими тілами, що перебувають у дотику.
2. Тертя руху (кінематичне тертя) проявляється під час відносного переміщення тіл.
Тертя спокою проявляється при спробах викликати відносний рух тіл, що дотикаються. Якщо до тіла, яке перебуває на певній плоскій поверхні, прикласти деяку паралельну до межі розділу силу, то тіло зберігатиме стан спокою до тих пір, доки величина цієї сили не перевищить деяке значення 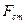 :
: 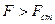 . Силу
. Силу 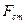 називають силою статичного тертя.
називають силою статичного тертя.
Дослідним шляхом було встановлено, що величина сили статичного тертя пропорційна силі нормального тиску тіла на опорну поверхню і залежить від природи і стану поверхонь, які дотикаються:
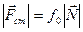 , або
, або 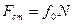 (3.4)
(3.4)
У виразі (3.4) 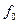 – коефіцієнт статичного тертя. На момент початку взаємного переміщення тіл тертя спокою переходить у тертяковзання, яке описується виразом, подібним до (3.4)
– коефіцієнт статичного тертя. На момент початку взаємного переміщення тіл тертя спокою переходить у тертяковзання, яке описується виразом, подібним до (3.4)
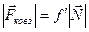 , або
, або 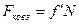 , (3.5)
, (3.5)
де 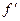 – коефіцієнт тертя ковзання. За малих швидкостей
– коефіцієнт тертя ковзання. За малих швидкостей 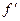
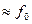 .
.
До динамічних сил тертя належать також сили тертякочення. Сили тертя кочення значно менші від сил тертя ковзання. Для сил тертя кочення виконується закон Кулона:
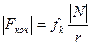 , (3.6)
, (3.6)
тут 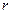 – радіус поверхні тіла, що котиться, а
– радіус поверхні тіла, що котиться, а 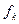 – коефіцієнт тертя кочення.
– коефіцієнт тертя кочення.
Всередині течії рідини або газу виникають сили внутрішнього (в’язкого) тертя, зумовлені дією сил міжмолекулярного зчеплення на межі різних шарів та передаванням імпульсу з одного шару в інший. Ісаак Ньютон експериментально встановив, що сила внутрішнього тертя між шарами пропорційна до градієнта швидкості 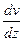 та площі шару
та площі шару 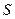 (рис.6):
(рис.6):
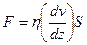 , (3.7)
, (3.7)
 де
де 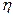 – в’язкість (коефіцієнт внутрішнього тертя рідини), яка чисельно дорівнює силі внутрішнього тертя між шарами одиничної площі при одиничному градієнті швидкості.
– в’язкість (коефіцієнт внутрішнього тертя рідини), яка чисельно дорівнює силі внутрішнього тертя між шарами одиничної площі при одиничному градієнті швидкості.
Градієнт швидкості 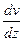 – визначає зміну величини швидкості на одиницю відстані у напрямку, перпендикулярному до вектора швидкості,
– визначає зміну величини швидкості на одиницю відстані у напрямку, перпендикулярному до вектора швидкості,
Під час руху твердих тіл у рідині або газі виникають сили опору середовищ, які ще називають силами лобового опору. За невеликих швидкостей сила лобового опору пропорційна до швидкості руху тіла:
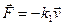 . (3.8)
. (3.8)
Знак мінус вказує, що сила опору має напрямок протилежний до швидкості взаємного руху. За доволі великих швидкостей має місце квадратична залежність сили опору від швидкості:
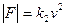 . (3.9)
. (3.9)
Якщо ж швидкість взаємного руху перевищує швидкість поширення звуку в даній рідині (газі), то залежність сили тертя від  є кубічною:
є кубічною:
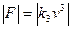 (3.10)
(3.10)
3.3 Пружні сили
Під дією зовнішніх сил тіла можуть змінювати свою форму та об’єм, тобто деформуватися. Для твердих тіл розрізняють два граничні випадки деформацій: пружні і пластичні. Пружна деформація зникає після припинення дії деформуючої сили, пластична деформація частково або повністю зберігається після припинення дії деформуючої сили.
Пружні сили, які виникають у тілі як протидія деформуючій силі, мають електромагнітну природу. За пружної деформації найближче оточення атома чи молекули не змінюється, а тому міжмолекулярна взаємодія призводить до повернення системи у початковий стан після припинення дії деформуючої сили. За умови пластичної деформації у тілі відбуваються незворотні зміни, при яких порушується характерна взаємодія між атомами, відстань між атомами стає настільки великою, що не можуть повністю відновитися відповідні міжатомні зв’язки, які забезпечують стійкість твердого тіла.
Механічні внутрішні сили, що виникають у деформованому тілі, зазвичай характеризують механічним напруженням – пружною силою, яка припадає на одиницю площі поперечного перерізу тіла:
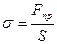 (3.11)
(3.11)
Основними видами деформацій є деформації розтягу, стиску, згину, зсуву та кручення.
3.3.1 Деформація розтягу (стиску). Закон Гука
Деформація розтягу (стиску) є однією з найпростіших деформації, за якої тіло зазнає зміни довжини, завдяки дії поздовжньої зовнішньої сили 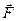 . Якщо під дією сили
. Якщо під дією сили 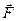 довжина тіла змінилась від
довжина тіла змінилась від 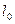 до
до 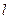 , то
, то 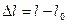 називають абсолютним видовженням, а
називають абсолютним видовженням, а 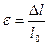 – відносним видовженням. Для деформації розтягу
– відносним видовженням. Для деформації розтягу 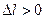 , а для деформації стиску
, а для деформації стиску 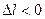 .
.
Дослідним шляхом встановлено, що при незначних деформаціях зміна довжини тіла пропорційна прикладеній силі 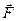 (закон Гука, рис.7):
(закон Гука, рис.7):
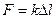 (3.12)
(3.12)
Тут 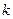 – коефіцієнт жорсткості тіла.
– коефіцієнт жорсткості тіла.
Під час деформації розтягу (стиску) у речовині виникає внутрішнє механічне напруження, що протидіє зовнішній силі 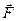 . Механічне напруження
. Механічне напруження 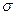 чисельно дорівнює силі пружності, яка діє на одиницю площі перерізу тіла
чисельно дорівнює силі пружності, яка діє на одиницю площі перерізу тіла
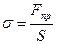 . (3.13)
. (3.13)
 Тому закон Гука для поздовжніх деформацій звичайно записують у вигляді:
Тому закон Гука для поздовжніх деформацій звичайно записують у вигляді:
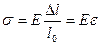 , (3.14)
, (3.14)
де 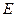 – модуль Юнга, коефіцієнт пропорційності, який чисельно дорівнює механічному напруженню, за якого
– модуль Юнга, коефіцієнт пропорційності, який чисельно дорівнює механічному напруженню, за якого 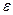 = 1. Модуль Юнга є важливою характеристикою пружних властивостей речовини. Відзначимо, що для абсолютної більшості речовин досягти видовження
= 1. Модуль Юнга є важливою характеристикою пружних властивостей речовини. Відзначимо, що для абсолютної більшості речовин досягти видовження 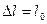 неможливо внаслідок виникнення пластичної деформації і подальшого руйнування зразка.
неможливо внаслідок виникнення пластичної деформації і подальшого руйнування зразка.
За деформацій розтягу та стиску відбувається також зміна поперечних розмірів тіла. Цю зміну розмірів характеризують відносним поперечним стиском або розтягом: 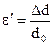 ,
, 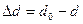 (рис.7).Тут
(рис.7).Тут 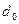 – величина, що характеризує поперечні розміри тіла (товщина чи ширина зразка) до деформації,
– величина, що характеризує поперечні розміри тіла (товщина чи ширина зразка) до деформації, 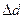 – зміна згаданої величини
– зміна згаданої величини 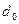 при деформації.
при деформації.
Відношення відносної поперечної деформації 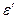 до відповідної їй поздовжньої відносної деформації
до відповідної їй поздовжньої відносної деформації 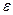 називають коефіцієнтом Пуасона:
називають коефіцієнтом Пуасона:
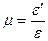 (3.15)
(3.15)
Подібно до модуля Юнга 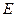 коефіцієнт Пуасона характеризує пружні властивості матеріалу тіла. Для більшості металів
коефіцієнт Пуасона характеризує пружні властивості матеріалу тіла. Для більшості металів 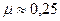 .
.
Вище згадувалося, що при значних видовженнях мають місце поява пластичної деформації та руйнування зразка. Схематично типову діаграму розтягу зразка показано на рис.8.
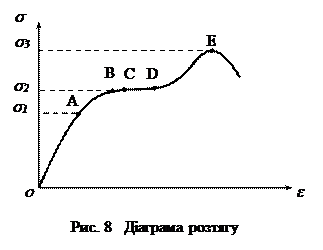 |
З цього рисунка видно, що закон Гука (лінійна залежність
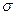 від
від 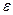 ) виконується у межах від О до точки А, від А до B деформація ще пружна, однак лінійна залежність
) виконується у межах від О до точки А, від А до B деформація ще пружна, однак лінійна залежність 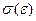 порушується. Точка B відповідає межі пружності. На ділянці ВС виникають залишкові деформації. Точка С – межа текучості (звичайно відповідає залишковій деформації 0,2%). Ділянка СD – область текучості. Матеріали, для яких практично відсутня ділянка CD називають крихкими (цегла, скло,...). Під час подальшого розтягу тіла воно знову чинить опір розтягу (ділянка DE). Коли механічне напруження
порушується. Точка B відповідає межі пружності. На ділянці ВС виникають залишкові деформації. Точка С – межа текучості (звичайно відповідає залишковій деформації 0,2%). Ділянка СD – область текучості. Матеріали, для яких практично відсутня ділянка CD називають крихкими (цегла, скло,...). Під час подальшого розтягу тіла воно знову чинить опір розтягу (ділянка DE). Коли механічне напруження 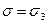 тіло починає руйнуватись. Напруження
тіло починає руйнуватись. Напруження 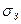 (точка Е) називають межею міцності даного матеріалу. Пружність і пластичність тіл залежать від температури, тиску та інших умов, у яких тіла перебувають.
(точка Е) називають межею міцності даного матеріалу. Пружність і пластичність тіл залежать від температури, тиску та інших умов, у яких тіла перебувають.
3.3.2 Деформації зсуву, кручення та згину.
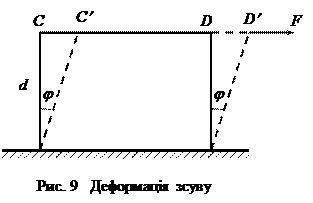 |
Деформація зсуву відбувається під дією сили, прикладеної дотично до поверхні тіла. Для прикладу розглянемо деформацію бруска у формі паралелепіпеда товщиною
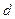 , виготовленого з однорідної ізотропної речовини (рис.9).
, виготовленого з однорідної ізотропної речовини (рис.9).
Нижня грань АВ бруска жорстко закріплена, а до верхньої CD прикладена сила F , яка паралельна до неї. Під дією сили F грань CD зсувається у положення 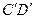 . За малих деформацій можна не враховувати зміни товщини зразка. Тому вважаємо, що всі шари зразка зсунулися на деякий малий кут
. За малих деформацій можна не враховувати зміни товщини зразка. Тому вважаємо, що всі шари зразка зсунулися на деякий малий кут 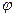 , причому
, причому 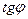 =
= 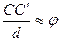 . Кут
. Кут 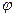 називають відносним зсувом. Якщо вважати, що сила F рівномірно розподілена по площі верхньої грані, то у будь якому перерізі, паралельному даній грані, існує тангенціальне напруження
називають відносним зсувом. Якщо вважати, що сила F рівномірно розподілена по площі верхньої грані, то у будь якому перерізі, паралельному даній грані, існує тангенціальне напруження 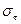 =
= 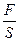 , де S –площа верхньої грані.
, де S –площа верхньої грані.
Закон Гука для пружної деформації зсуву можна сформулювати так: тангенціальне механічне напруження під час пружної деформації зсуву прямо пропорційне до відносного зсуву:
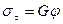 , (3.15)
, (3.15)
де G – модуль зсуву. Модуль Юнга Е і модуль зсуву G взаємопов’язані. Зокрема, для більшості ізотропних тіл G=0,4Е.
Деформації розтягу (стиску) і зсуву належать до однорідних деформацій, за яких всі малі елементи тіла деформовані однаково. При неоднорідних деформаціях (кручення і згин) деформації різних ділянок тіла неоднакові.
Розглянемо деформацію однорідної циліндричної дротини під дією пари сил 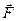 , прикладених до верхнього перерізу дротини (рис.10). Сили F створюють обертальний момент, під дією якого дротина зазнає деформації кручення: верхня основа дротини повернеться відносно закріпленої нижньої на кут
, прикладених до верхнього перерізу дротини (рис.10). Сили F створюють обертальний момент, під дією якого дротина зазнає деформації кручення: верхня основа дротини повернеться відносно закріпленої нижньої на кут 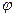 . Закон Гука для деформації кручення запишемо у вигляді:
. Закон Гука для деформації кручення запишемо у вигляді:
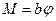 , (3.16)
, (3.16)
 |
де
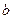 – модуль кручення, величина стала для даного зразка і залежна від його геометричних розмірів. Зокрема, для циліндричної дротини довжини
– модуль кручення, величина стала для даного зразка і залежна від його геометричних розмірів. Зокрема, для циліндричної дротини довжини 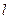 і радіуса
і радіуса 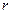 модуль кручення:
модуль кручення:
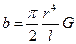 , (3.17)
, (3.17)
де G – модуль зсуву.
Деформація згину більш складна, оскільки під час згину окремі частини тіла зазнають деформації розтягу, інші – стиску, що в результаті супроводжується ще й деформацією зсуву. Проаналізуємо це на прикладі деформації згину паралелепіпеда, умовно розділеного лінією ВВ1 на два шари (рис.11).
З рисунка видно, що шари, які лежать нижче лінії ВВ1, зазнають деформації стиску, а шари, розташовані вище даної лінії – деформації розтягу. Оскільки відносне видовження (чи стиск) окремих початково горизонтальних ділянок різний, то в системі виникає ще й деформація зсуву.
 |
4 Робота та енергія
4.1 Робота, енергія, кінетична енергія
З другого закону Ньютона випливає, що в результаті дії сили тіло набуває деякого прискорення, тобто змінює швидкість, а відповідно і свій імпульс. Виникає питання характеристики впливу сили на певній ділянці траєкторії за скінчений проміжок часу. Для цього корисно ввести поняття роботи сили. Роботою сили 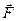 , що діє на матеріальну точку масою
, що діє на матеріальну точку масою 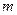 під час її переміщення на
під час її переміщення на 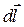 , називають фізичну величину, що чисельно дорівнює скалярному добутку цих величин (рис. 12):
, називають фізичну величину, що чисельно дорівнює скалярному добутку цих величин (рис. 12):
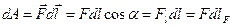 (4.1)
(4.1)
 В загальному випадку скінченого переміщення, коли можливі зміни величини і напрямку сили
В загальному випадку скінченого переміщення, коли можливі зміни величини і напрямку сили 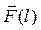 та самого напрямку переміщення, робота виконана на даній ділянці шляху визначається шляхом інтегрування
та самого напрямку переміщення, робота виконана на даній ділянці шляху визначається шляхом інтегрування
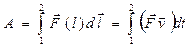 , (4.2)
, (4.2)
де 1, 2 – відповідно величини, що характеризують координати початкового і кінцевого положення тіла.
Робота, виконана силою за одиницю часу, називається потужністю: 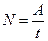 , або
, або 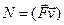 .
.
За одиницю роботи прийнято величину 1 Дж, що дорівнює роботі сили 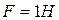 на шляху
на шляху 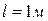 :
: 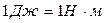 . Одиницею потужності є
. Одиницею потужності є 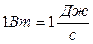 .
.
В загальному випадку 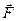 і
і 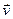 не колінеарні, тобто сила
не колінеарні, тобто сила 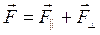 . Оскільки
. Оскільки 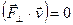 , то роботу виконує лише складова
, то роботу виконує лише складова 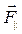 , то.
, то.
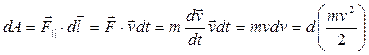 .
.
Тоді, на підставі (4.2), повна робота, виконана на скінченій ділянці шляху, дорівнює:
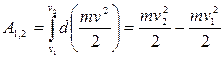 . (4.3)
. (4.3)
Величини 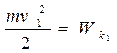 і
і 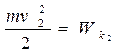 описують стан тіла масою
описують стан тіла масою 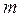 в початковій і кінцевій точках траєкторії. Величину
в початковій і кінцевій точках траєкторії. Величину 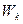 називають кінетичною енергією тіла. В результаті виконання роботи силою
називають кінетичною енергією тіла. В результаті виконання роботи силою 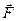 відбулася зміна кінетичної енергії тіла, тобто
відбулася зміна кінетичної енергії тіла, тобто
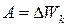 . (4.3¢)
. (4.3¢)
Складова сили, перпендикулярна до вектора швидкості, роботи не виконує, а тому вона не призводить до зміни кінетичної енергії. Прикладом таких сил є доцентрова (відцентрова) сила: 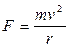 та сила Лоренца, яка діє на заряджену частинку при її русі в магнітному полі:
та сила Лоренца, яка діє на заряджену частинку при її русі в магнітному полі: 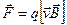 , де
, де 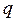 - заряд частинки,
- заряд частинки, 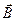 - індукція магнітного поля.
- індукція магнітного поля.
Енергія тіла характеризує його здатність виконати роботу. Проілюструємо це наступним прикладом. Нехай тіло масою 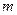 , яке рухається з швидкістю
, яке рухається з швидкістю 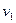 , налітає на нерухоме тіло і протягом деякого проміжку часу
, налітає на нерухоме тіло і протягом деякого проміжку часу 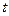 з постійною силою штовхає це тіло (про це має свідчити рівносповільнений рух першого тіла з прискоренням
з постійною силою штовхає це тіло (про це має свідчити рівносповільнений рух першого тіла з прискоренням 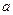 ). За час
). За час 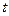 швидкість першого тіла зменшилась з
швидкість першого тіла зменшилась з 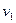 до
до 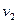 :
: 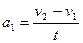 . При цьому початково нерухоме тіло перемістилося на відстань
. При цьому початково нерухоме тіло перемістилося на відстань 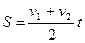 , оскільки рух цього тіла також рівноприскорений з прискоренням
, оскільки рух цього тіла також рівноприскорений з прискоренням 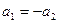 . На друге тіло з боку першого тіла протягом часу
. На друге тіло з боку першого тіла протягом часу 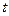 діяла сила
діяла сила 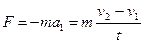 , яка виконала роботу:
, яка виконала роботу:
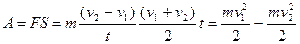 (4.4)
(4.4)
Таким чином, за рахунок кінетичної енергії першого тіла виконана робота для переміщення та зміни швидкості другого тіла.
4.2 Кінетична енергія обертального руху
а). Кінетична енергія обертального руху матеріальної точки.
Кінетична енергія матеріальної точки визначається її масою та швидкістю: 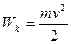 . Якщо частинка здійснює рух по колу, не приймаючи участі в інших рухах, то в даному виразі
. Якщо частинка здійснює рух по колу, не приймаючи участі в інших рухах, то в даному виразі 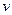 є лінійною швидкістю обертового руху і
є лінійною швидкістю обертового руху і 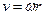 , де
, де 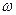 – кутова швидкість обертового руху, а
– кутова швидкість обертового руху, а 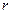 – радіус кола. Таким чином
– радіус кола. Таким чином
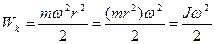 , (4.5)
, (4.5)
де 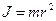 – момент інерції матеріальної точки відносно центра обертання.
– момент інерції матеріальної точки відносно центра обертання.
б) Кінетична енергія обертального руху абсолютно твердого тіла навколо нерухомої осі.
Кінетична енергія довільного руху абсолютно твердого тіла дорівнює сумі кінетичних енергій усіх 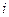 матеріальних точок, з яких складається тіло:
матеріальних точок, з яких складається тіло:
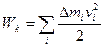 (4.6)
(4.6)
Якщо тіло здійснює лише обертовий рух довкруги нерухомої осі, то швидкість 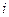 – тої матеріальної точки
– тої матеріальної точки 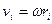 , де
, де 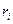 – відстань точки від осі обертання. Таким чином:
– відстань точки від осі обертання. Таким чином:
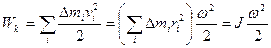 , (4.7)
, (4.7)
де 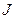 – момент інерції тіла відносно осі обертання.
– момент інерції тіла відносно осі обертання.
Якщо тіло обертається з кутовою швидкістю 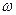 довкруги осі, яка проходить через центр інерції і одночасно здійснює поступальний рух з швидкістю
довкруги осі, яка проходить через центр інерції і одночасно здійснює поступальний рух з швидкістю 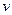 , то сумарна кінетична енергія руху тіла дорівнює:
, то сумарна кінетична енергія руху тіла дорівнює:
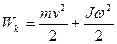 (4.8)
(4.8)
Прикладами подібного руху можуть бути рухи обруча або однорідного диска однакових мас 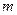 , і радіуса
, і радіуса 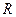 що котяться рівномірно горизонтальною ділянкою з однаковими швидкостями поступального руху:
що котяться рівномірно горизонтальною ділянкою з однаковими швидкостями поступального руху:
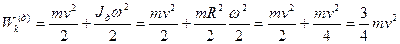
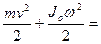
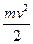 +
+ 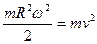 .
.
Тобто  , бо
, бо 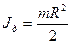 , а
, а 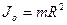
4.3 Консервативні сили. Потенціальна енергія
Якщо на тіло в кожній точці вибраної області простору діє сила певної фізичної природи, то кажуть, що тіло перебуває у силовому полі. Серед існуючих макроскопічних силових полів розрізняють поля трьох типів, математичні описи яких різні: поля консервативні, поля дисипативні та поля гіроскопічних сил.
Консервативними (потенціальними) силовими полями є такі силові поля, в яких робота під час переміщення тіла з деякої точки простору в іншу не залежить від вигляду траєкторії, а залежить лише від координат початку і кінця переміщення. З цього випливає, що в полі консервативних сил робота, виконана під час переміщення тіла вздовж довільної замкненої траєкторії, дорівнює нулеві:
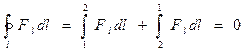 (4.9)
(4.9)
В даному виразі позначення 1 і 2 не є межами інтегрування, а лише вказують, що робота виконана під час переміщенні тіла з початкового положення1 у кінцеве 2 і навпаки.
Відзначимо, що консервативними є поле сил тяжіння, електростатичне поле та поле пружних сил (у межах застосовності закону Гука).
До неконсервативних сил належать сили дисипативні та гіроскопічні сили.
Дисипативними називають такі сили, повна робота яких при довільних рухах тіла в замкнутій системі завжди негативна. Дисипативними є сили тертя і опору, дія яких супроводжується дисипацією (розсіюванням) енергії. Характерною властивістю дисипативних сил є те, що робота виконана ними залежить не лише від початкової і кінцевої координати здійсненого переміщення, але і від вигляду траєкторії. Тому робота цих сил на довільній замкненій траєкторії завжди відмінна від нуля:
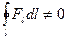 (4.10)
(4.10)
Іншим типом неконсервативних сил є гіроскопічні сили: це сили, що залежать від швидкості матеріальної точки і завжди перпендикулярні до неї:
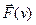 ^
^ 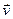 .
.
Очевидно, що робота гіроскопічних сил завжди дорівнює нулю, оскільки 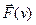 ^
^ 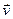 , то відповідно і
, то відповідно і 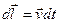 ^
^ 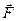 . Тоді
. Тоді
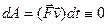
Прикладами гіроскопічних сил є згадана вище сила Лоренца, яка діє на заряджену частинку в магнітному полі та сила Коріоліса, що діє на тіло під час його руху в системі відліку, яка обертається відносно інерціальної системи відліку.
В полі консервативних сил робота, яка виконується під час переміщення тіла визначається як різниця двох величин, одна з яких залежить лише від координати кінцевого положення 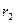 , а інша від координати початкового положення
, а інша від координати початкового положення 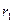 . Тобто:
. Тобто:
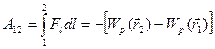 (4.11)
(4.11)
Величину 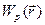 назвемо потенціальною енергією тіла в даній точці з координатою
назвемо потенціальною енергією тіла в даній точці з координатою 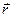 поля консервативних сил.
поля консервативних сил. 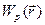 – скалярна функція, яка має сенс енергії взаємодії сил поля з даним тілом. З виразу (4.11) випливає, що зміна потенціальної енергії тіла в полі консервативних сил чисельно дорівнює роботі, виконаній силами поля під час переміщення тіла:
– скалярна функція, яка має сенс енергії взаємодії сил поля з даним тілом. З виразу (4.11) випливає, що зміна потенціальної енергії тіла в полі консервативних сил чисельно дорівнює роботі, виконаній силами поля під час переміщення тіла:
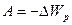 (4.12).
(4.12).
Потенціальну енергію звичайно визначають з точністю до деякого постійного доданка, оскільки у виразі для роботи фіксується зміна 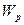 , а тому
, а тому
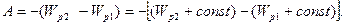
Як згадувалося вище, консервативними є сили гравітаційні, електростатичні та пружні. Розглянемо деякі конкретні приклади розрахунку потенціальної енергії тіл.
4.4 Центрально – симетричне поле
Силове поле називають центральним, якщо в усіх його точках сили, що діють на тіла, внесені у це поле, напрямлені вздовж прямих, які перетинаються в певній точці – центрі сил. Центральне поле називається сферично - (центрально -) симетричним, якщо числове значення сили, що діє на тіло, залежить тільки від відстані r від центра сил.
Силові поля, що характеризують гравітаційну взаємодію точкових мас або електростатичну взаємодію точкових зарядів, є центрально - симетричними. Це видно із запису законів Ньютона для гравітаційної сили та закону Кулона для взаємодії точкових зарядів:
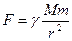 (4.13)
(4.13)
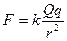 (4.14)
(4.14)
Нагадаємо, що 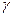 – гравітаційна стала; M і m – маси матеріальних точок; r – відстань між взаємодіючими тілами; k– електрична стала, залежна від вибору системи одиниць; Q і q– величина точкових зарядів.
– гравітаційна стала; M і m – маси матеріальних точок; r – відстань між взаємодіючими тілами; k– електрична стала, залежна від вибору системи одиниць; Q і q– величина точкових зарядів.
Запис виразів (4.13) і (4.14) у векторній формі дозволяє стверджувати, що сила взаємодії 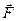 паралельна чи антипаралельна
паралельна чи антипаралельна 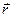 (в залежності від притягання чи відштовхування тіл), тобто
(в залежності від притягання чи відштовхування тіл), тобто 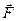 лежить на прямій проведеній з центра до точки спостереження.
лежить на прямій проведеній з центра до точки спостереження.
В полі гравітаційних сил 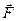 і
і 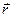 антипаралельні (має місце притягання):
антипаралельні (має місце притягання):
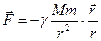 (4.15)
(4.15)
Покажемо, що центрально – симетричне поле консервативне і знайдемо потенціальну енергію тіла в цьому полі.
Розглянемо взаємодію двох матеріальних точок масами 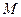 та
та 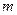 . Нехай
. Нехай 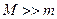 , початок координат співпадає з точкою масою
, початок координат співпадає з точкою масою 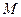 , а координата точки
, а координата точки 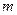 задається радіус-вектором
задається радіус-вектором 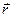 . Вважаємо, що між тілами діють лише сили гравітаційного притягання і тіло масою
. Вважаємо, що між тілами діють лише сили гравітаційного притягання і тіло масою 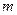 переміщається в полі закріпленого тіла масою
переміщається в полі закріпленого тіла масою
