Пружні хвилі
Хвилею називають процес поширення коливань в просторі.
Пружна хвиля – процес поширення механічних коливань у пружному середовищі. На відміну від електромагнітних хвиль, які можуть поширюватися як в речовині так і у вакуумі, для поширення механічних коливань необхідне середовище, яке чинить опір розтягу (стиску) чи зсуву. Розглянемо основні характеристики хвильових процесів, що описують поширення гармонійних коливань у просторі.
8.1 Характеристики хвиль
Основними характеристиками, що визначають властивості хвиль довільної природи є частота коливань 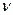 і швидкість поширення хвилі v. В природі існують хвилі поздовжні та поперечні. В поздовжній хвилі коливання фізичної величини (в механіці – коливання частинок речовини) відбувається в тому ж напрямку, в якому поширюються хвилі. В поперечній хвилі коливання відбуваються в напрямку, перпендикулярному до напрямку поширення хвилі.
і швидкість поширення хвилі v. В природі існують хвилі поздовжні та поперечні. В поздовжній хвилі коливання фізичної величини (в механіці – коливання частинок речовини) відбувається в тому ж напрямку, в якому поширюються хвилі. В поперечній хвилі коливання відбуваються в напрямку, перпендикулярному до напрямку поширення хвилі.
В механіці поздовжні хвилі існують в усіх середовищах, в яких виникають пружні сили під час деформацій розтягу і стиску. Таким чином, поздовжні хвилі можуть поширюватись в газах, рідинах і твердих тілах.
Поперечні пружні механічні хвилі можуть існувати лише в твердих тілах, де наявні пружні сили при деформаціях зсуву. Однак хвилі за своїм характером близькі до поперечних хвиль у пружних твердих тілах, можуть виникати на поверхні рідини або на межі двох рідин. Виникнення цих хвиль обумовлене не пружними силами в рідині, а дією сили тяжіння. Якщо в деякій точці поверхня рідини буде порушена (наприклад, на поверхню впало точкове тіло), то на поверхні рідини поширюються імпульси, викликані ударом. При цьому частинки рідини рухаються не лише вертикально, але й горизонтально. Хвиля, строго кажучи, не буде поперечною. Однак, якщо не враховувати рух окремих частинок рідини і лише спостерігати за рухом поверхні рідини, то ми отримаємо картину поширення поперечного імпульсу. Як згадувалось, при поширенні цього імпульсу сила тяжіння і сили поверхневого натягу відіграють роль, аналогічну до дії пружних сил при поширенні поперечних коливань в твердому тілі.
При поширенні хвилі в пружному середовищі має місце передавання імпульсу (енергії) від частинок, що коливаються до сусідніх частинок, які також почнуть коливатись, хоч і з деяким запізненням. Геометричне місце точок, до яких коливання дійшли до даного моменту часу називають фронтом хвилі. Очевидно, що у всіх точках фронту хвилі коливання проходять в однакових фазах. При поширенні хвиль з точкового джерела в однорідному ізотропному середовищі фронтом хвилі є сфера.
Швидкість руху фронту хвилі в напрямку поширення хвилі називають фазовою швидкістю v (тобто швидкістю поширення постійної фази коливань). За один період коливань Т фронт хвилі поширюється на відстань 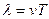 .
. 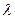 називають довжиною хвилі.
називають довжиною хвилі.
Оскільки коливні процеси відзначаються періодичністю, то при неперервній дії джерела коливань процес поширення коливань буде тривалим і в певній ділянці простору будуть спостерігатися коливні процеси, початкова фаза яких буде залежати від координати точки спостереження. На поверхнях, які в початкові моменти відповідали певним положенням фронту хвилі коливання в усіх точках будуть відбуватись в однакових фазах. Ці поверхні називають хвильовими поверхнями.
Отже, хвильова поверхня – геометричне місце точок, у яких коливання відбуваються в однакових фазах. Очевидно, що фронт хвилі є також хвильовою поверхнею. Наслідком із сказаного є наступне: довжина хвилі – найкоротша відстань між двома сусідніми хвильовими поверхнями, в яких коливання проходять в однакових фазах.
Взагалі кажучи, хвильова поверхня може мати різну форму. Зокрема, при поширенні хвиль в неоднорідному середовищі форма хвильової поверхні може змінюватись. Для простоти розгляду будемо аналізувати хвилі, в яких форма хвильової поверхні найпростіша. Плоска хвиля – хвильова поверхня є площиною, перпендикулярною до 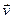 .
.
Сферична хвиля – хвильова поверхня сфера, а сукупність можливих хвильових поверхонь є системою концентричних сфер.
8.2 Рівняння хвилі
Знайдемо рівняння, яке б повністю описувало коливний рух в межах хвилі, подібно як рівняння 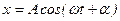 описує гармонійне коливання матеріальної точки.
описує гармонійне коливання матеріальної точки.
Шукаємо рівняння функції 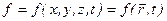 , яка має наступні властивості. При фіксації координати точки спостереження дана функція повинна перетворитися в рівняння коливань в даній точці:
, яка має наступні властивості. При фіксації координати точки спостереження дана функція повинна перетворитися в рівняння коливань в даній точці:
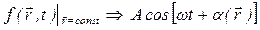 ,
,
Де 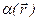 – початкова фаза коливань, залежна від координати.
– початкова фаза коливань, залежна від координати.
З іншого боку, якщо в 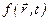 зафіксувати час
зафіксувати час 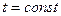 , то дана функція повинна дати миттєву картину коливного процесу в усій ділянці простору, в якій існує хвиля.
, то дана функція повинна дати миттєву картину коливного процесу в усій ділянці простору, в якій існує хвиля.
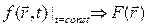
Очевидно, що і по координаті 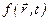 повинна бути періодичною функцією, оскільки однакова фаза коливань хвилі повторюється через відстані рівні довжині хвилі
повинна бути періодичною функцією, оскільки однакова фаза коливань хвилі повторюється через відстані рівні довжині хвилі 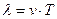 .
.
Знайдемо рівняння плоскої хвилі, тобто хвилі, в якій фронт хвилі і всі хвильові поверхні є площинами, перпендикулярними до вектора швидкості 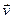 .
.
Джерелом плоскої хвилі може бути плоске протяжне джерело. Нехай джерело плоскої хвилі лежить в площині 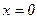 і періодично зміщує частинки середовища в цій площині з круговою частотою
і періодично зміщує частинки середовища в цій площині з круговою частотою 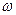 . Це означає, що в площині
. Це означає, що в площині 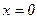 збуджуються гармонійні коливання
збуджуються гармонійні коливання
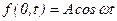 (8.1)
(8.1)
Внаслідок пружного зв’язку між частинками середовища в середовищі в напрямку ox будуть поширюватись коливання з швидкістю 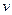 . До площини з координатою
. До площини з координатою 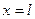 коливання надійдуть із запізненням
коливання надійдуть із запізненням 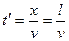 .
.
 |
Тому рівняння коливань в точці
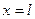 буде мати вигляд:
буде мати вигляд:
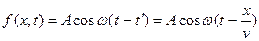 (8.2)
(8.2)
Рівняння (8.2) називають рівнянням плоскої хвилі, що поширюється в напрямку осі x.
Оскільки 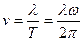 , рівняння (8.2) можна перетворити до вигляду :
, рівняння (8.2) можна перетворити до вигляду :
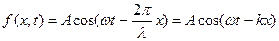 (8.3)
(8.3)
де 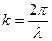 – хвильове число.
– хвильове число.
Для плоскої хвилі, що поширюється з початку координат 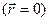 з плоского джерела, довільно орієнтованого в просторі рівняння хвилі може бути записане:
з плоского джерела, довільно орієнтованого в просторі рівняння хвилі може бути записане:
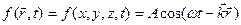 (8.4)
(8.4)
В даному виразі 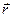 – координата точки спостереження коливань,
– координата точки спостереження коливань, 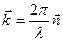 – хвильовий вектор,
– хвильовий вектор, 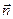 – одиничний вектор нормалі до поверхні джерела коливань. Вираз (8.4) можна записати в такій формі:
– одиничний вектор нормалі до поверхні джерела коливань. Вираз (8.4) можна записати в такій формі:
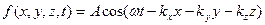 (8.5)
(8.5)
Для рівняння сферичної хвилі, що поширюється з точкового джерела з координатою 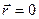 , отримують:
, отримують:
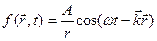 (8.6)
(8.6)
де А – величина, чисельно рівна амплітуді коливань на відстані 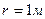 від джерела коливань.
від джерела коливань.
8.3 Хвильове рівняння
Рівняння коливань 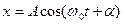 є розв’язком рівняння руху, зведеного до вигляду:
є розв’язком рівняння руху, зведеного до вигляду:
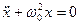 (7.7)
(7.7)
Знайдемо диференціальне рівняння, розв’язком якого є рівняння хвилі. Для цього знайдемо другі часткові похідні по змінних 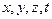 від виразу (8.5):
від виразу (8.5):
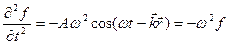 (8.7)
(8.7)
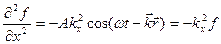 (8.8)
(8.8)
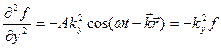 (8.9)
(8.9)
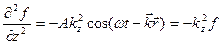 (8.10)
(8.10)
Після додавання рівнянь (8.8), (8.9) і (8.10) отримаємо:
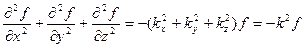 (8.11)
(8.11)
Якщо з виразу (8.7) знайти f і підставити у (8.11) маємо:
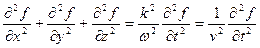 , (8.12)
, (8.12)
оскільки 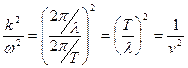 .
.
Рівняння (8.12) називають хвильовим рівнянням. Розв’язком цього рівняння є рівняння хвилі.
8.4 Швидкість поширення пружних хвиль в середовищі
Швидкість поширення хвиль зумовлена швидкістю передавання коливального руху від частинки до частинки середовища. Запишемо швидкість поширення поздовжньої пружної хвилі в довільному пружному суцільному середовищі. В загальному випадку незалежно від агрегатного стану пружного середовища (тверде тіло, рідина чи газ) для швидкості поширення поздовжньої хвилі можна отримати:
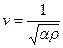 (8.13)
(8.13)
де 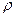 – густина недеформованого середовища,
– густина недеформованого середовища, 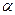 – коефіцієнт пружності.
– коефіцієнт пружності.
Для поширення поздовжньої хвилі в твердому тілі коефіцієнт пружності виразимо через модуль Юнга: 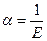 і для
і для  v отримаємо:
v отримаємо:
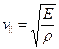 (8.14)
(8.14)
В рідинах і газах швидкість поширення поздовжніх хвиль визначається з допомогою виразу:
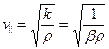 (8.15)
(8.15)
де k – модуль об’ємного стиску, 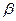 – адіабатичний[5] коефіцієнт об’ємного стиску. (Для води
– адіабатичний[5] коефіцієнт об’ємного стиску. (Для води 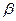 зменшується з підвищенням температури, а відповідно v збільшується).
зменшується з підвищенням температури, а відповідно v збільшується).
Швидкість поширення хвиль в газах визначається з допомогою формули:
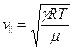 (8.16)
(8.16)
де R – універсальна газова стала, 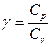 – відношення молярних теплоємностей газу відповідно при сталому тиску Ср і сталому об’ємі Сv. (
– відношення молярних теплоємностей газу відповідно при сталому тиску Ср і сталому об’ємі Сv. ( 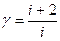 , де і – число ступенів вільностімолекули газу); μ – маса моля газу. З (8.16) видно, що
, де і – число ступенів вільностімолекули газу); μ – маса моля газу. З (8.16) видно, що 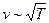 і обернене до
і обернене до 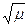 .
.
Наприклад, швидкості поширення звуку (повздовжньої хвилі) у водні та кисні відносяться між собою як:
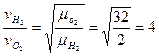
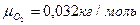 ,
, 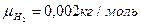
При поширенні поперечної хвилі у твердому тілі швидкість її поширення може бути розрахована з допомогою виразу подібного до (8.14):
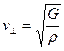 , (8.17)
, (8.17)
де 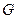 - модуль зсуву.
- модуль зсуву.
Оскільки величина G менша за модуль Юнга, то очевидно, що 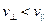 .
.
8.5 Енергія пружних хвиль
Знайдемо енергію, яку несе хвиля в пружному середовищі. Розглянемо плоску хвилю, що поширюється в напрямку x:
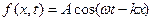
Виділимо в середовищі об’єм 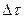 настільки малий, щоб в цьому об’ємі всі частинки речовини коливались в однаковій фазі, маючи при цьому однакову швидкість. Кінетична енергія хвильового руху в даному об’ємі:
настільки малий, щоб в цьому об’ємі всі частинки речовини коливались в однаковій фазі, маючи при цьому однакову швидкість. Кінетична енергія хвильового руху в даному об’ємі:
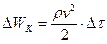 , (8.18)
, (8.18)
де 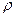 - густина середовища.
- густина середовища.
Швидкість частинок
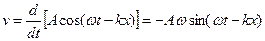
Таким чином, кінетичну енергію DWK обчислимо:
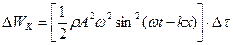 (8.19)
(8.19)
Середнє значення кінетичної енергії 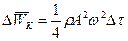 .
.
По аналогії з міркуваннями про середні кінетичну та потенціальну енергії гармонійного коливання (§7.2) можна показати, що
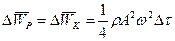 .
.
Повна середня механічна енергія
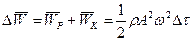
Середня механічна енергія, що припадає на одиницю об’єму (густина енергії) середовища, в якому поширюється хвиля
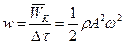 (8.20)
(8.20)
В напрямку свого поширення хвиля несе з собою деяку енергію. Густина потоку енергії, що несе хвиля:
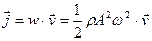 (8.21)
(8.21)
Густина потоку 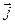 - це кількість енергії, яку переносить хвиля за одиницю часу через одиничний плоский переріз (
- це кількість енергії, яку переносить хвиля за одиницю часу через одиничний плоский переріз ( 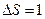 ), перпендикулярний до напрямку поширення хвилі.
), перпендикулярний до напрямку поширення хвилі.
Через довільну поверхню S хвиля за одиницю часу несе енергію
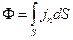 (8.22)
(8.22)
(інтеграл взято по цілій поверхні S).
8.6 Інтерференція хвиль. Стояча хвиля
Якщо в середовищі поширюються одночасно декілька хвиль, то коливання частинок середовища є геометричною сумою коливань, які б здійснювали ці частинки під дією кожної з хвиль зокрема. Коливання під дією хвиль додаються одне з одним, не збурюючи самих хвиль. Додавання даного типу називаються суперпозицією хвиль.
Найбільш цікавим є додавання коливань, збурених хвилями з однаковою циклічною частотою ( 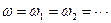 ) і постійною різницею фаз між коливаннями в кожній точці, де спостерігається додавання коливань. Такі хвилі називають когерентними, а додавання коливань, збурених когерентними хвилями, інтерференцією хвиль.
) і постійною різницею фаз між коливаннями в кожній точці, де спостерігається додавання коливань. Такі хвилі називають когерентними, а додавання коливань, збурених когерентними хвилями, інтерференцією хвиль.
Окремим випадком інтерференції є накладання двох зустрічних когерентних хвиль з однаковими амплітудами. При цьому в середовищі виникає коливний процес, що називається стоячою хвилею. Стоячу хвилю можна отримати при додаванні хвиль, одна з яких поширюється в певному напрямку (наприклад, Х), а інша виникла при відбиванні першої хвилі від деякої перешкоди.
Запишемо рівняння двох зустрічних когерентних хвиль і знайдемо їх суму:
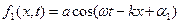 і
і 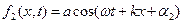
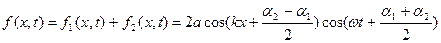 (8.23)
(8.23)
Рівняння (8.23) є рівнянням стоячої хвилі. З даного виразу видно, що сумарне коливання здійснюється з циклічною частотою 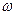 , а амплітуда коливань залежить від координати. Для зручності обговорення виразу виберемо початок відліку координати Х таким чином, щоб
, а амплітуда коливань залежить від координати. Для зручності обговорення виразу виберемо початок відліку координати Х таким чином, щоб 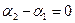 , а початок відліку часу t таким, щоб
, а початок відліку часу t таким, щоб 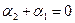 (реально це
(реально це 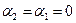 ). При цьому вираз (8.23) запишеться у вигляді:
). При цьому вираз (8.23) запишеться у вигляді:
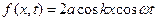 (8.24)
(8.24)
В точках х для яких 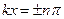 амплітуда коливань набуває максимального значення і дорівнює 2а (бо
амплітуда коливань набуває максимального значення і дорівнює 2а (бо 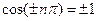 ). Такі точки називають пучностями:
). Такі точки називають пучностями:
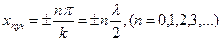 (8.25)
(8.25)
оскільки 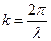 . Відзначимо, що пучність є не окремою точкою, а площиною, рівняння якої
. Відзначимо, що пучність є не окремою точкою, а площиною, рівняння якої 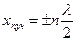 . В площинах, координати яких
. В площинах, координати яких
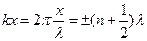 , (
, ( 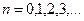 ), (8.25)
), (8.25)
амплітуда коливань дорівнює нулю. Дані точки називають вузлами:
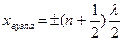 (8.26)
(8.26)
З наведених виразів видно, що відстань між сусідніми вузлами рівна 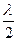 , відстані між сусідніми пучностями також
, відстані між сусідніми пучностями також 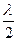 , а відстань між сусідніми вузлом і пучністю дорівнює
, а відстань між сусідніми вузлом і пучністю дорівнює 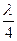 .
.
З виразу, що описує залежність амплітуди коливань в стоячій хвилі від координати 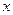 :
:
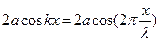
можна зробити висновок, що коливання в точках по різні боки від площини вузла відбуваються в протифазі. В ділянці від одного вузла до наступного коливання відбуваються в однаковій фазі.
Характерною особливістю стоячої хвилі є те, що в даній хвилі немає передавання енергії від одних точок середовища до інших, як це відбувається у біжучій хвилі. Окрім того у вузлах коливання відсутні.
Для виникнення стоячої хвилі в обмеженому середовищі необхідне узгодження частоти коливань джерела хвилі з відповідним характерним розміром середовища (наприклад, з довжиною об’єкта l вздовж якого поширюються пряма і відбита хвилі). Покажемо це на прикладі поперечних коливань стрижня, закріпленого в одній точці, та коливань струни, закріпленої в обох кінцях.
 |
Якщо один кінець стрижня довжиною l закріпити, а по іншому кінцю (незакріпленому) вдарити молотком перпендикулярно до l, то всередині стрижня виникне стояча хвиля поперечних коливань (рис. 52), причому в закріпленому кінці стрижня буде вузол, а на вільному – пучність. Стояча хвиля поздовжніх коливань може виникнути в стрижні при ударі в торець стрижня.
Між довжиною стрижня l і довжиною стоячої хвилі l виконується співвідношення:
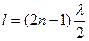 ,
, 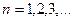 (8.27)
(8.27)
(в довжину стрижня повинна вкладатись непарна кількість 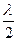 ). Власні частоти коливання стрижня наступні:
). Власні частоти коливання стрижня наступні:
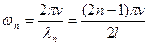 , (8.28)
, (8.28)
або 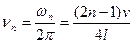 (8.28а)
(8.28а)
де 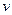 – фазова швидкість поширення поперечної чи поздовжньої хвилі в матеріалі стрижня,
– фазова швидкість поширення поперечної чи поздовжньої хвилі в матеріалі стрижня, 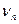 - частота коливань.
- частота коливань.
В закріпленій в обох кінцях струні вузли коливань будуть в точках закріплення струни
 |
Тому по довжині струни завжди повинна вкладатись парна кількість
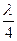 :
:
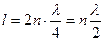 ,
, 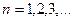 (8.29)
(8.29)
Відповідно циклічна частота, що відповідає можливим стоячим хвилям:
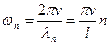 (8.30)
(8.30)
Частоти коливань 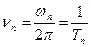 струни називають власними частотами:
струни називають власними частотами:
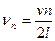 (8.31)
(8.31)
Усі власні частоти кратні 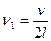 , яку називають основною частотою. Власні частоти
, яку називають основною частотою. Власні частоти 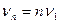 називаються гармоніками.
називаються гармоніками.
Подібний результат можна отримати і для поширення поздовжніх коливань у розглянутому вище однорідному стрижні або стовпі рідини чи газу довжиною 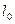 . У цьому випадку напрямок пружних коливань частинок речовини співпадає з напрямком поширення прямої та відбитої хвиль
. У цьому випадку напрямок пружних коливань частинок речовини співпадає з напрямком поширення прямої та відбитої хвиль 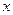 . Нехай джерело коливань (джерело біжучої прямої хвилі) перебуває у площині
. Нехай джерело коливань (джерело біжучої прямої хвилі) перебуває у площині 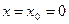 . У даній площині є пучність коливань, а у протилежному кінці проміжку довжиною
. У даній площині є пучність коливань, а у протилежному кінці проміжку довжиною 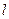 відбувається відбивання біжучої хвилі і при
відбувається відбивання біжучої хвилі і при 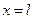 є вузол коливань. У стоячій хвилі у проміжок довжиною
є вузол коливань. У стоячій хвилі у проміжок довжиною 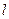 повинна вкладатись непарна кількість
повинна вкладатись непарна кількість 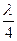 , тобто
, тобто 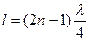 . Власними частотами коливань у стоячій хвилі даної конфігурації є частоти:
. Власними частотами коливань у стоячій хвилі даної конфігурації є частоти:
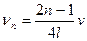 ,
, 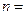 1,2,3,... (8.28а)
1,2,3,... (8.28а)
і відповідне рівняння коливань, аналогічне (8.24):
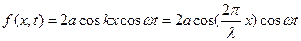
Проаналізуємо останній вираз при 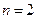 (тобто, при
(тобто, при 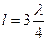 . Для цього знайдемо вирази і побудуємо графіки для амплітуд коливань
. Для цього знайдемо вирази і побудуємо графіки для амплітуд коливань 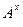 , максимальних швидкостей частинок
, максимальних швидкостей частинок 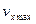 , кінетичних та потенціальних енергій частинок. Пам’ятаємо, що зміщення частинок при коливаннях відбувається у напрямку
, кінетичних та потенціальних енергій частинок. Пам’ятаємо, що зміщення частинок при коливаннях відбувається у напрямку 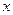 і амплітуда коливань запишеться:
і амплітуда коливань запишеться:
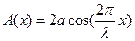 .
.
Відповідно, швидкість частинок
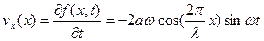 ,
,
а тому 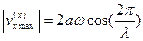 .
.
Максимальна кінетична енергія частинок:
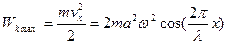 ,
,
а максимальна потенціальна енергія частинок середовища у полі пружних сил:
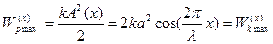 .
.
Відзначимо, що коливання 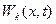 та
та 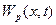 в часі проходять таким чином, що при фіксованому
в часі проходять таким чином, що при фіксованому 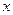 :
:
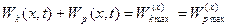
В точках 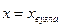 повна енергія коливань дорівнює нулю, бо у цих точках незалежно від
повна енергія коливань дорівнює нулю, бо у цих точках незалежно від 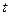 амплітуда коливань, а тому і швидкість руху частинок, дорівнюють нулю.
амплітуда коливань, а тому і швидкість руху частинок, дорівнюють нулю.
8.7 Дифракція хвиль
Дифракцією називають сукупність явищ, пов’язаних із поширенням хвиль у середовищі з наявними у ньому перешкодами чи неоднорідностями скінчених розмірів. Зокрема, одним з проявів дифракції є огинання хвилею перешкод, розміри яких сумірні з довжиною хвилі.
Пояснення дифракційних явищ базується на принципі Гюйгенса - Френеля, суть якого полягає у тому, що довільна точка фронту хвилі є джерелом вторинної хвилі, вторинні ж хвилі когерентні і можуть інтерферувати.
Принцип Гюйгенса - Френеля дозволяє пояснити поширення хвиль довільної фізичної природи в ізотропних, неоднорідних та анізотропних середовищах, а також отримати математичні вирази для закономірностей, що характеризують відбивання і заломлення хвиль на межі двох середовищ.
8.8 Звукові хвилі
Звуковими хвилями називають пружні хвилі з частотою коливань в межах від 16 Гц до 20000 Гц, що поширюються у суцільних середовищах і можуть сприйматися вухом людини. Пружні хвилі, частота коливань у яких більша за 20000 Гц, називають ультразвуковими, а пружні хвилі, частота яких менша за 16 Гц – інфразвуковими. Розділ фізики, у якому вивчають закономірності збудження, поширення, сприймання звукових хвиль та їх взаємодію з речовиною, називають акустикою.
Швидкість поширення звукових хвиль в різних середовищах визначається пружними властивостями середовища і не залежить від частоти коливання у хвилі. Нагадаємо, що у твердих тілах поширюються поздовжні і поперечні звукові хвилі, швидкості поширення яких даються виразами (8.14) та (8.17):
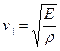 ,
, 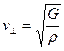 .
.
У рідинах і газах поширюються лише поздовжні хвилі, швидкості поширення яких даються виразами (8.15): 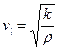 і, зокрема для газів,(8.15) може бути зведений до вигляду:
і, зокрема для газів,(8.15) може бути зведений до вигляду: 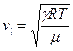 , тобто (8.16).
, тобто (8.16).
Ділянку середовища, у якій поширюються звукові хвилі, називають звуковим полем. При поширенні звукових хвиль має місце перенесення енергії у напрямку їх поширення. Інтенсивністю або силою звуку називають величину, що чисельно дорівнює середній енергії 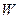 , яку переносить звукова хвиля через одиничну площадку
, яку переносить звукова хвиля через одиничну площадку  , перпендикулярну до напрямку поширення звукової хвилі, за одиницю часу:
, перпендикулярну до напрямку поширення звукової хвилі, за одиницю часу:
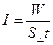 (8.32)
(8.32)
Мінімальну силу звуку, яку ще може сприйняти вухо людини, називають порогом чутності. Поріг чутності для людського вуха залежить від частоти коливань. Найбільша чутливість вуха людини є у діапазоні частот 1000-3000 Гц. Для об’єктивної оцінки, незалежної від чутності вуха конкретної людини, за поріг чутності вибрана величина 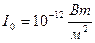 , достатньо близька до реального порогу в згаданому діапазоні частот.
, достатньо близька до реального порогу в згаданому діапазоні частот.
Силу звуку, вище якої втрачається відчуття звуку і настає больове відчуття, називають порогом больового відчуття. На рис. 54 показано залежність порогу чутності і порогу больового відчуття від частоти звукових коливань.
Область інтенсивностей звуку, обмежену наведеними кривими, називають областю чутності. З рис. 54 видно, що людське вухо слабо відчуває зміну 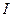 . А тому, оскільки значення
. А тому, оскільки значення 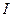 , наведені на рис. 54 суттєво (на декілька порядків величини) відрізняються між собою, зручно ввести величини, що є логарифмами від
, наведені на рис. 54 суттєво (на декілька порядків величини) відрізняються між собою, зручно ввести величини, що є логарифмами від 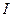 . Для цього вводять поняття рівня сили звуку (фізіологічно: рівень гучності):
. Для цього вводять поняття рівня сили звуку (фізіологічно: рівень гучності):
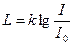 , (8.33)
, (8.33)
де 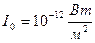 ,
, 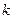 – коефіцієнт пропорційності.
– коефіцієнт пропорційності.
 Вибір коефіцієнта
Вибір коефіцієнта 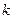 довільний. Якщо взяти
довільний. Якщо взяти  , то рівень сили звуку виразиться в одиницях, що називають „Бел”. На практиці використовують
, то рівень сили звуку виразиться в одиницях, що називають „Бел”. На практиці використовують 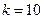 і тоді вираз (8.33) записується у вигляді:
і тоді вираз (8.33) записується у вигляді:
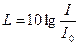 (8.34)
(8.34)
Одиницею рівня сили звуку при даному записі 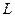 буде величина децибел (дБ), яка у 10 разів менша за Бел.
буде величина децибел (дБ), яка у 10 разів менша за Бел.
Дата добавления: 2015-09-11; просмотров: 4586;
