Переріз кривих поверхонь площиною

При перетині кривих поверхонь площиною утворюється плоска фігура, яку називають перерізом.

У загальному випадку для побудови лінії перерізу кривої поверхні площиною необхідно виконати такі дії:

1 Визначити, яке положення займає січна площина відносно площин проекцій. Якщо січна площина є проекціювальною, то одна проекція перерізу є готовою, вона збігається зі слідом заданої площини. Друга проекція будується за умовою належності точок перерізу поверхні. Якщо січна площина займає загальне положення, то задачу можна розв`язати методом заміни площин проекцій, або допоміжних січних посередників.

2 Для спрощення побудови лінії перерізу усі точки, через які проходить лінія перерізу, розділяють на опорні, точки перетину і проміжні точки.

3 Іноді січна площина не повністю перетинає задану поверхню, тоді для зручності зображення поверхні продовжують до повного перетину поверхні площиною, але потім умовну частину перерізу треба відкинути.

4 Видимість перерізу визначають за допомогою точок перетину, які належать обрисній твірній, головному меридіану або екватору.

5 Через отримані точки проводять плавну криву лінію перерізу, враховуючи при цьому її видимість.

При перерізі прямого колового циліндра площиною можливі такі випадки:

1 Якщо січна площина не перпендикулярна і не паралельна осі циліндра, то вона перетинає циліндр по еліпсу.

2 Якщо січна площина перпендикулярна осі циліндра, то отримаємо коло.

3 Якщо січна площина паралельна осі циліндра, то отримаємо прямокутник.

4 Якщо січна площина є дотичною до поверхні циліндра, то отримаємо пряму лінію.

На рис. 1.6.7 наведено приклад побудови перерізу поверхні циліндра фронтально проекціювальною площиною Т.

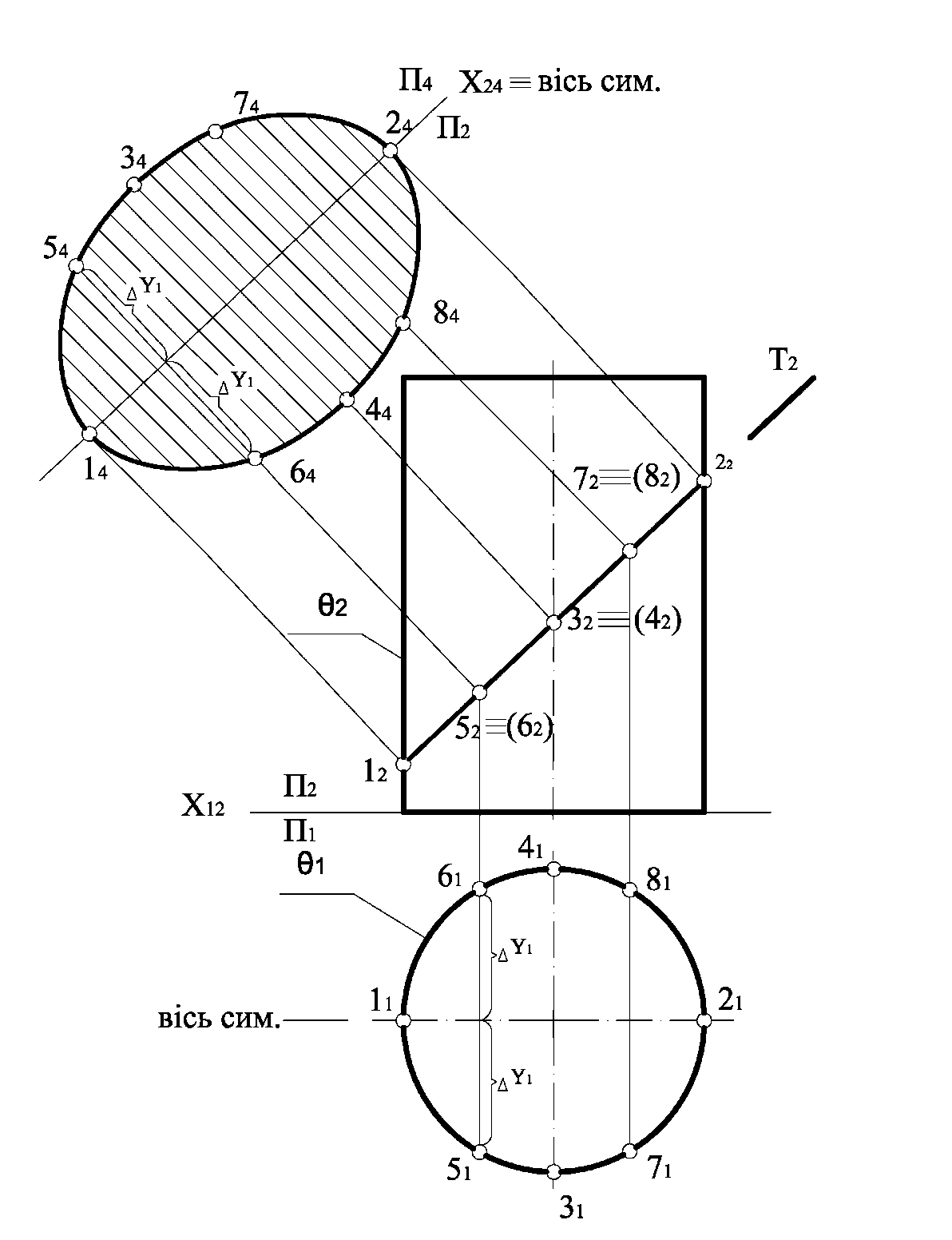
Рисунок 1.6.7

Завдяки збиральним властивостям проекціювальних площин на П₂ маємо готову проекцію лінії перерізу, яка збігається зі слідом площини Т (Т₂). Січна площина Т не перпендикулярна і не паралельна осі циліндра, вона перетинає циліндр по еліпсу. Велика вісь еліпсу належить площині головного меридіана циліндра 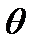і дорівнює відстані між точками 1₂ і 2₂, а мала вісь еліпсу належить площині профільного меридіана і дорівнює відстані між точками 3₁ і 4₁. Для точності побудови еліпсу вибираємо ще допоміжні проекції точок 5₂ і 6₂, а також 7₂ і 8₂. Далі для побудови натуральної величини перерізу циліндра нахиленою площиною Т використовуємо метод заміни площини проекцій. Вісь нової системи проекцій Х₂₄ будуємо паралельно Т₂. Координати точок еліпсу заміряємо з горизонтальної площини проекцій і переносимо на П₄. Завдяки тому, що еліпс є симетричною фігурою, координати точок краще заміряти від осі 1₁–2₁.

При перетині конуса січною площиною утворюються криві другого порядку.

На рис. 1.6.8 наведені всі можливі випадки розташування січної площини відносно визначника конічної поверхні.

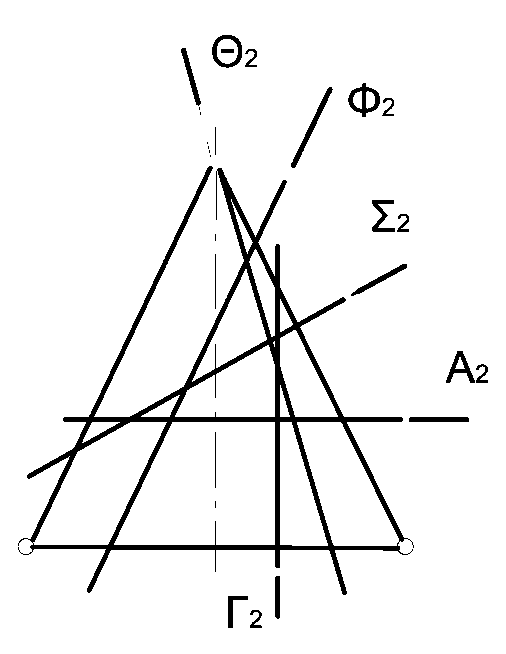
Рисунок 1.6.8

Якщо січна площина 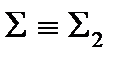перетинає всі твірні конуса, то отримаємо еліпс. При перетині конуса площиною 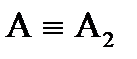перпендикулярно до осі конуса отримаємо коло. При перетині конуса площиною 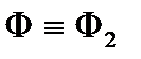паралельно одній із твірних отримаємо параболу. Якщо січна площина 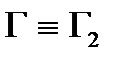перетинає поверхню конуса паралельно осі обертання або яким-небудь двом твірним, то отримаємо гіперболу. При перетині конуса площиною 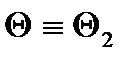, яка проведена через вершину конуса, отримаємо трикутник.

На рис. 1.6.9 наведено приклад побудови перерізу конуса фронтально проекціювальною площиною .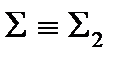

Площина 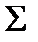має на П₂ збиральні властивості, тому фронтальна проекція еліпса є відрізком прямої 1₂ 2₂.

Горизонтальна проекція еліпса визначається за ознакою належності його точок поверхні конуса. Побудову горизонтальної проекції еліпса виконуємо з використанням допоміжних січних посередників – це горизонтальні площини рівня.

Велика вісь еліпса дорівнює відстані між точками 1₂ і 2₂, у яких січна площина перетинає обрисові твірні конуса. Якщо мала вісь знаходиться в площині перерізу і перпендикулярна великій осі еліпса, то вона є фронтально проекціювальною прямою.

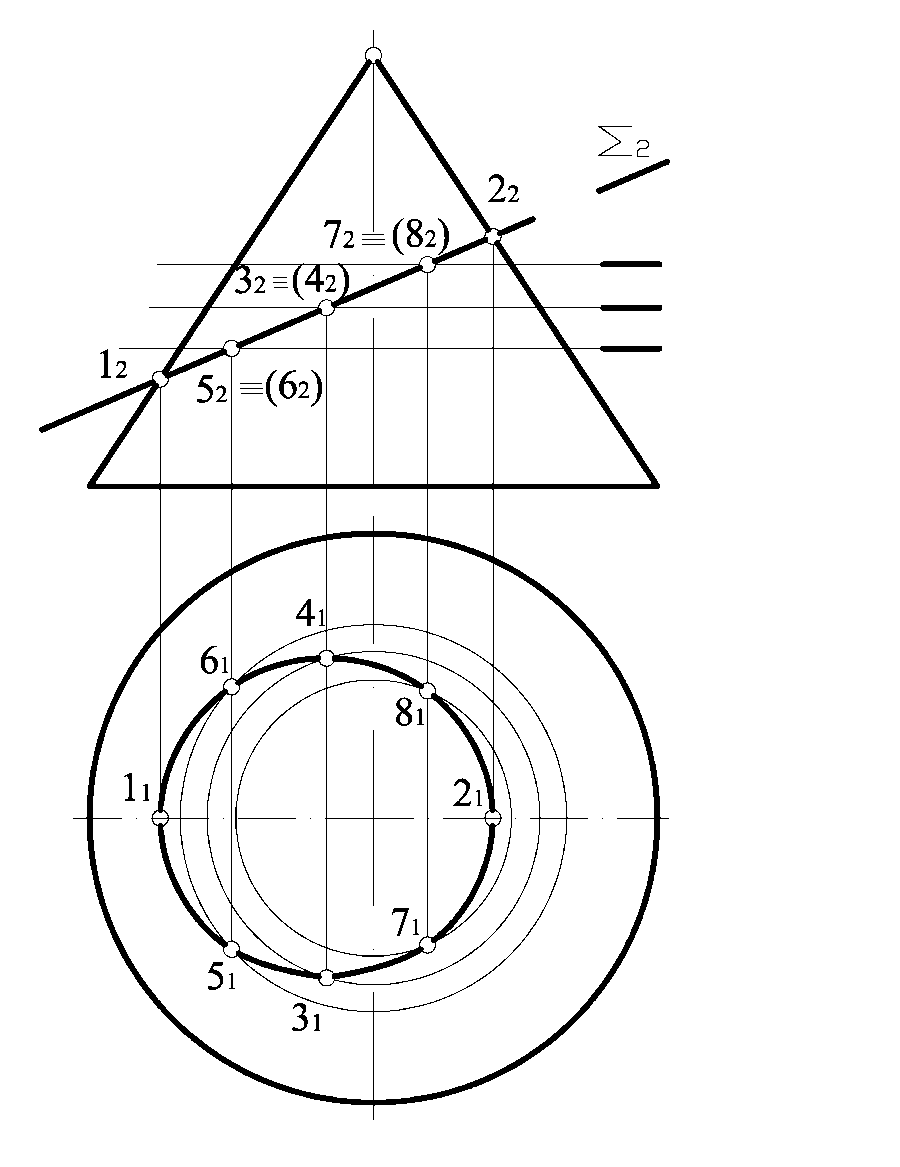
Рисунок 1.6.9

Для знаходження фронтальної проекції осі ділимо велику вісь 1₂2₂ на дві рівних частини і отримуємо точку 3₂ 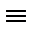(4₂), яка є фронтальною проекцією малої осі еліпса. Довільно вибираємо ще допоміжні точки 5₂ (6₂), а також 7₂ (8₂). Через задані точки проводимо допоміжні січні площини – це горизонтальні площини рівня, які перетинають конус по колу, будуємо ці кола на П₁ і, використовуючи вертикальну відповідальність, знаходимо горизонтальні проекції точок, через які будуємо плавну криву лінію – це горизонтальна проекція еліпса. Мала вісь еліпса дорівнює відстані між точками 3₁ і 4₁.