Переріз гранних поверхонь площиною
Перерізом називають плоску фігуру, яку отримують при перетині багатогранника площиною. Для побудови перерізів багатогранників використовують два способи: спосіб ребер, спосіб граней. Спосіб ребер передбачає розв’язання задачі на перетин прямої з площиною, причому виконується пошук точки перетину кожного бічного ребра з січною площиною.
Побудова перерізу значно спрощується, коли січна площина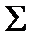 
є проекціювальною (рис. 1.5.7). У цьому випадку фронтальна проекція перерізу 12345 вже відома, оскільки вона збігається з фронтальним слідом січної фронтально проекціювальної площини 
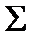. Горизонтальну проекцію перерізу будуємо за законом належності точки ребру і по вертикальній відповідності. Далі методом заміни площин проекцій перетворюємо площину перерізу, яка є проекціювальною в системі 
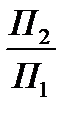, у площину рівня. Для цього будуємо вісь нової системи площин х24 ll 
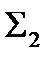. Координати точок перерізу заміряємо на П1 від осі х12 і переносимо відповідно на П4. Проекція площини перерізу 1424445434 є натуральною величиною.
На рис. 1.5.8 наведено приклад побудови перерізу похилої трикутної призми, яка перетинається фронтально проекціювальною площиною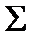 
.
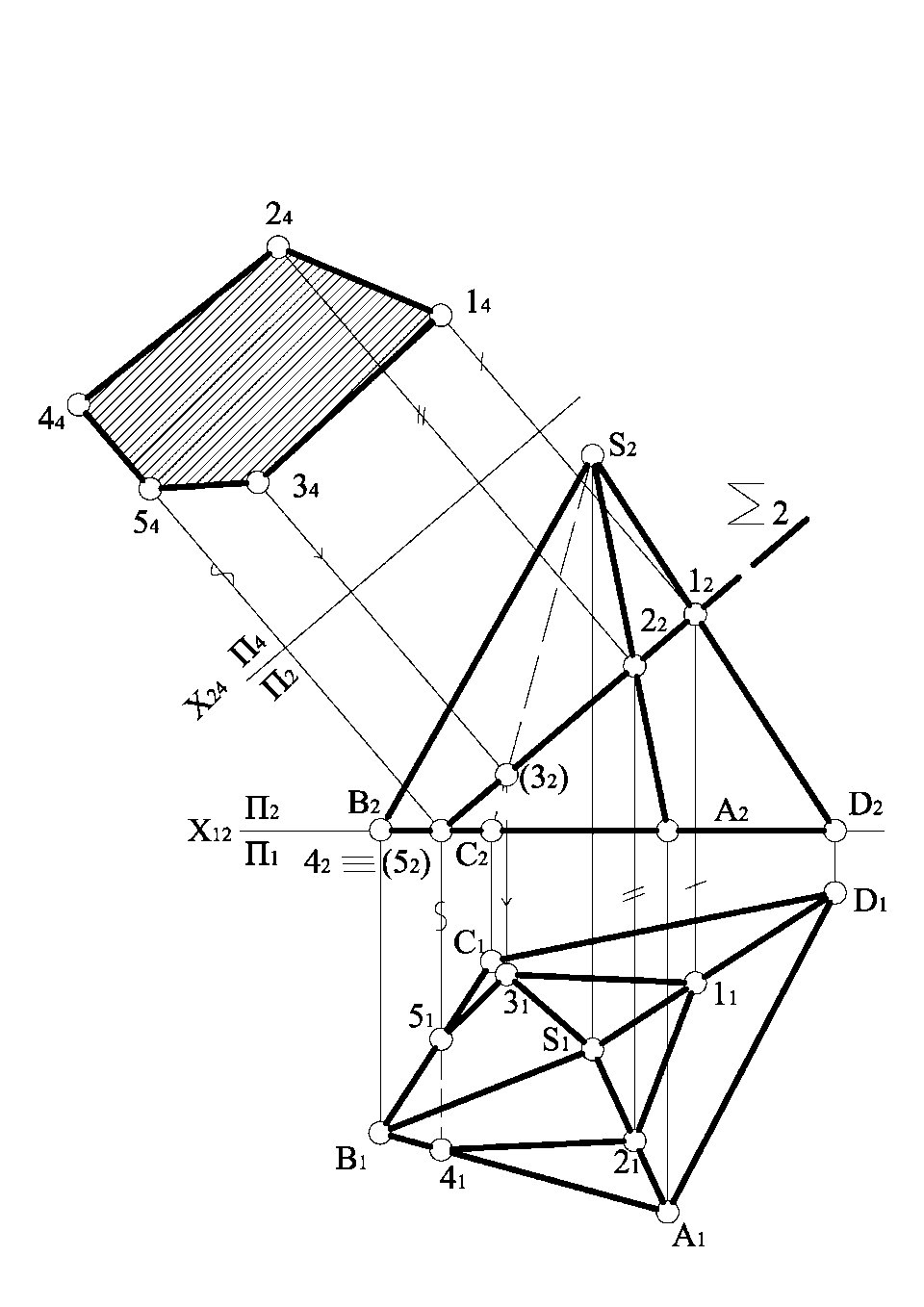
Рисунок 1.5.7
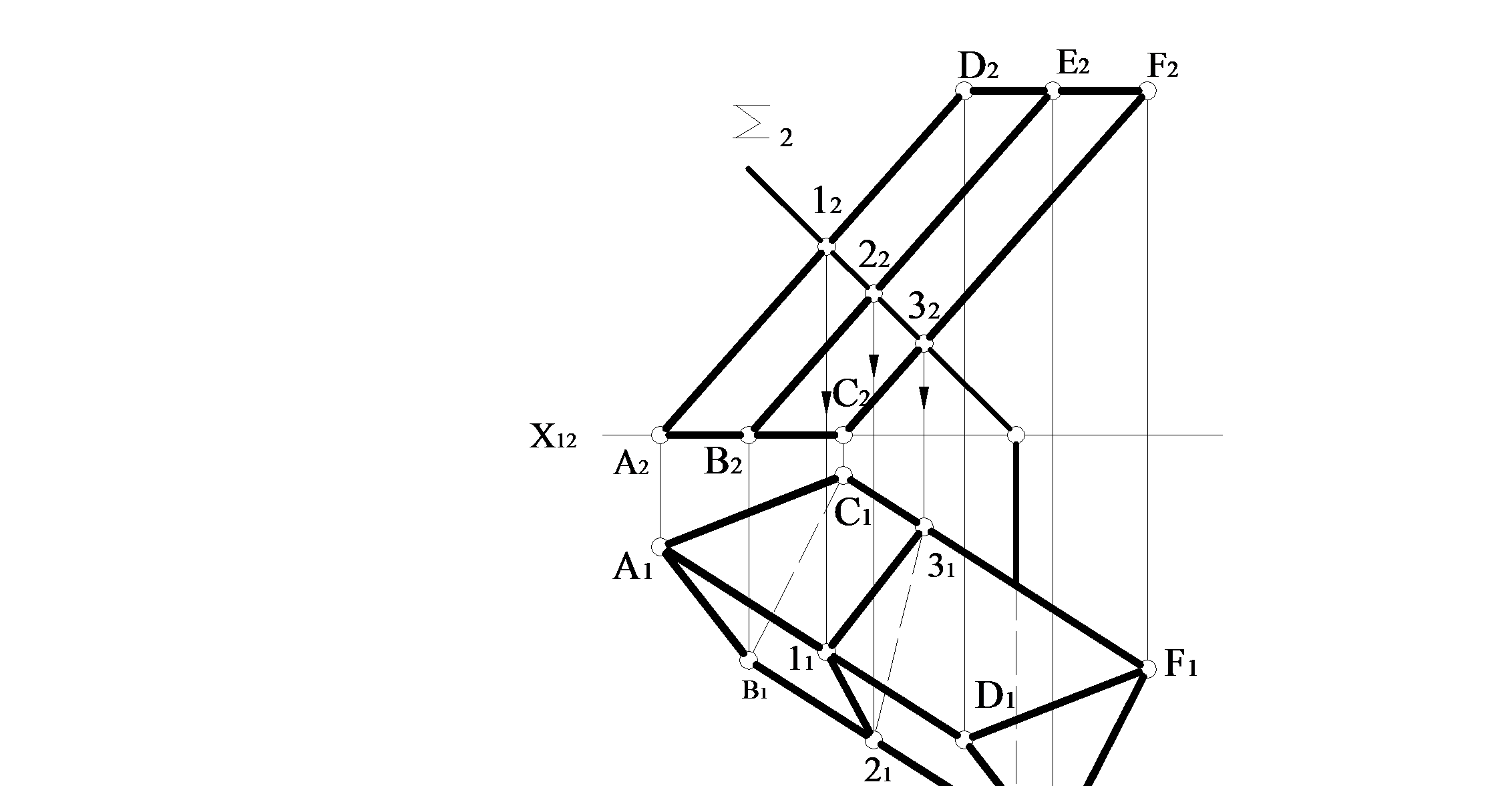
Рисунок 1.5.8
Фронтальна проекція площини перерізу 122232 збігається з фронтальним слідом площини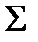 
. Горизонтальну проекцію перерізу визначаємо за допомогою вертикальної відповідності.
Дата добавления: 2015-09-11; просмотров: 923;