Метод заміни площин проекцій

У багатьох випадках розв’язання задачі значно спрощується, якщо прямі лінії, площини, елементи геометричних фігур займають окреме положення.

Переміщення геометричної фігури із загального положення в окреме можна виконати двома шляхами:

1 Переміщенням площин проекцій у положення, відносно яких плоскі фігури займали б окремі положення.

2 Переміщенням плоскої фігури в просторі в окреме положення відносно нерухомих площин проекцій.

Перший шлях лежить в основі методу заміни площин проекцій, а другий – в основі інших методів.

Суть методу полягає в тому, що самі геометричні фігури не змінюють свого положення, а в системі площин проекцій П₂ та П₁ послідовно замінюють одну, дві або більше площин проекцій. При цьому нова площина проекцій має бути перпендикулярною до тієї площини проекцій, яка залишається незмінною, а відносно плоских геометричних фігур вона повинна бути паралельною або перпендикулярною.

На рис. 1.4.1 зображена умовно перспективна модель проекціювання точки А на дві взаємно перпендикулярні площини проекцій П₁ та П₂, а також на додаткову площину П₄, яка перпендикулярна П₁. У результаті утворилась нова система площин проекцій 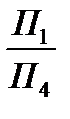зі своєю віссю проекцій х₁₄, як наслідок перетину площин проекцій П₁ та П₄. Положення горизонтальної проекції А₁ точки А залишається без зміни, оскільки точка А та площина П₁ не змінювали свого положення в просторі. Для знаходження нової фронтальної проекції точки А-А₄ достатньо виконати ортогональне проекціювання точки А на площину П₄. Відстань нової фронтальної проекції А₄ точки А від нової осі х₁₄ дорівнює відстані від старої фронтальної проекції А₂ точки А до старої осі х₁₂: .

Рисунок 1.4.1

Для побудови комплексного креслення нова площина проекцій П₄ обертається навколо осі х₁₄ до суміщення з горизонтальною площиною проекцій П₁ (рис. 1.4.2). Напрям обертання не впливає на результат розв’язання задачі. Обертання виконують таким чином, щоб не було накладання нових проекцій на старі.

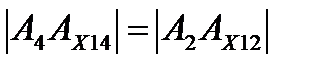
Рисунок 1.4.2

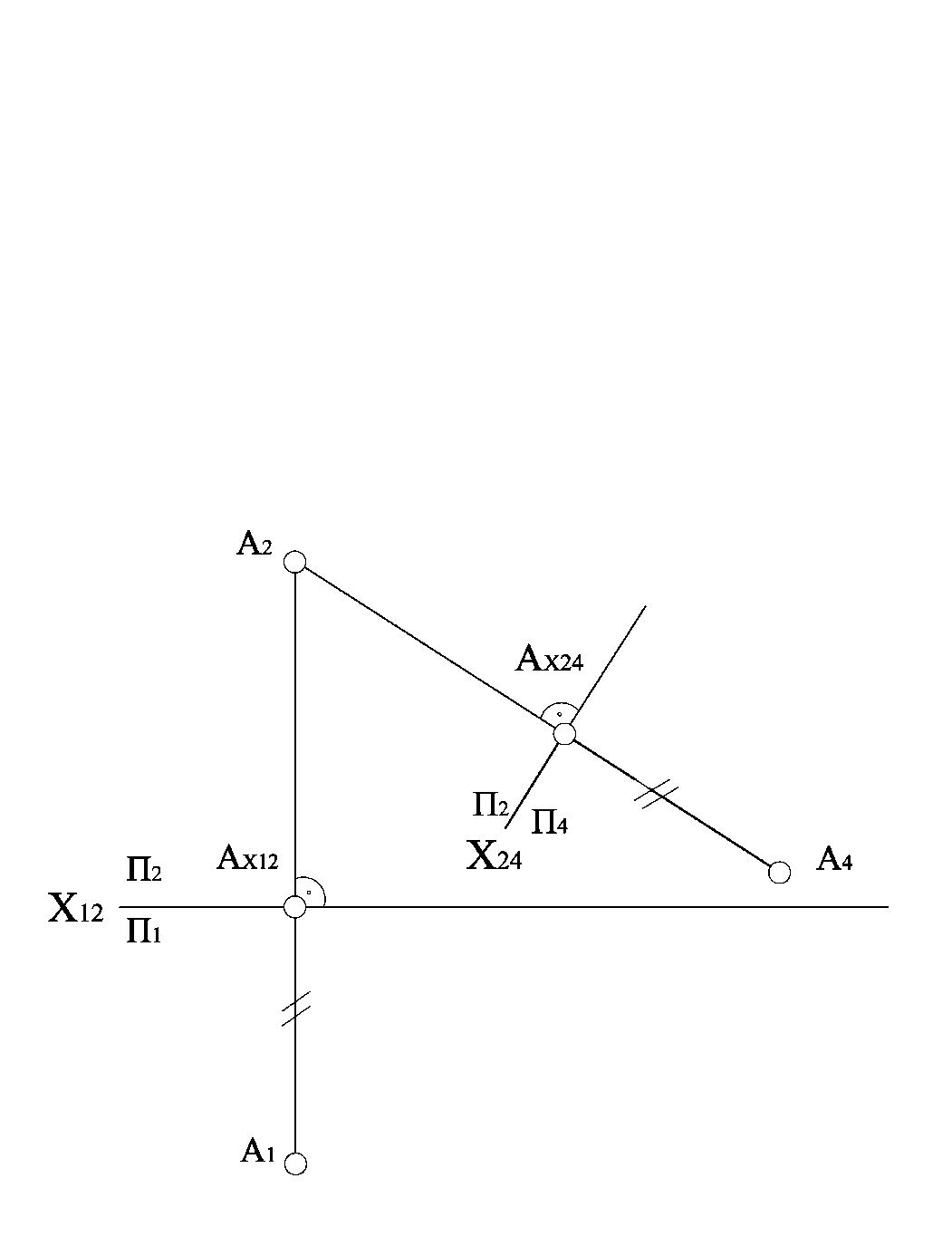
Заміна горизонтальної площини проекцій П₁ на нову площину П₄ та побудова нових проекцій точки А в системі відбувається аналогічно розглянутому випадку. Тепер без змін залишається фронтальна проекція точки, а для побудови нової горизонтальної проекції А₄ точки А необхідно зі старої фронтальної проекції точки опустити перпендикуляр (провести лінію зв’язку) на нову вісь х₂₄ та відкласти на ньому від точки перетину з віссю х₂₄ відрізок, що дорівнює відстані від горизонтальної проекції точки до осі х₁₂ (рис. 1.4.3).

Розв’язання всіх задач методом заміни площин проекцій зводиться до розв’язання чотирьох основних задач:

1 Перетворення прямої загального положення в пряму рівня.

2 Перетворення прямої загального положення в проекціювальну.

3 Перетворення площини загального положення в проекціювальну.

4 Перетворення площини загального положення в площину рівня.

На рис. 1.4.4 зображено розв’язання перших двох задач перетворення прямої загального положення в пряму рівня та перетворення її в проекціювальну. У системі 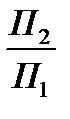відрізок прямої АВ займає загальне положення. Для перетворення відрізка прямої в пряму рівня будуємо на довільній відстані від відрізка площину П₄, яка паралельна проекції відрізка А₁В₁, а також ця площина .

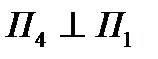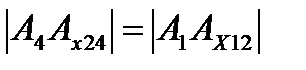
Рисунок 1.4.3

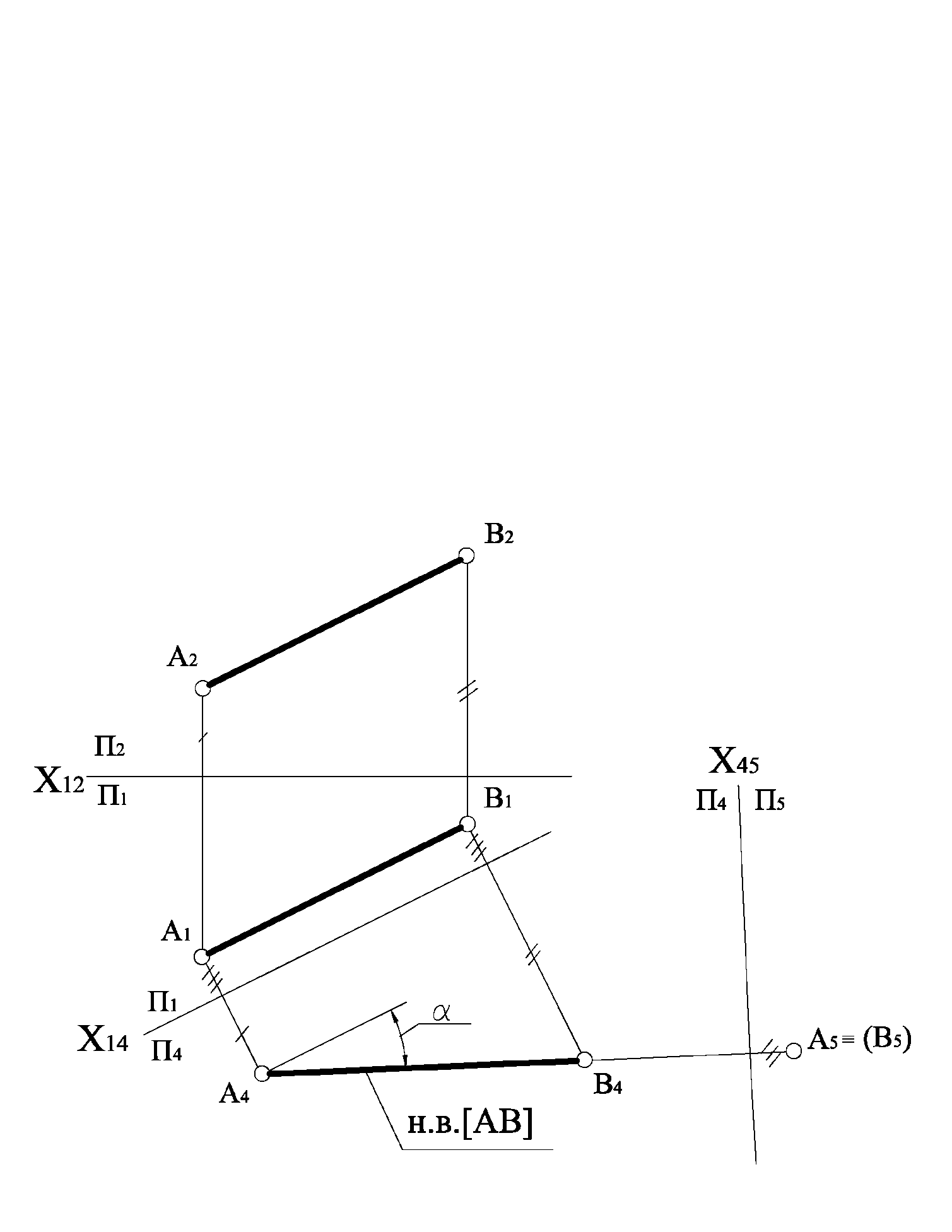
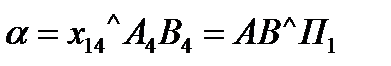
Рисунок 1.4.4

Щоб отримати натуральну величину відрізка, від осі х₁₄ відкладаємо відстані, що дорівнюють відстаням від точок А₂ і В₂ до осі х₁₂. У системі 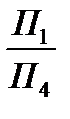відрізок прямої АВ стає прямою рівня і на площині проекцій П₄ проекціюється в натуральному вигляді.

Для перетворення відрізка прямої рівня в проекціювальне положення необхідно перпендикулярно до прямої рівня провести нову площину П₅, слідом якої буде х₄₅. Проекція прямої у вигляді точки 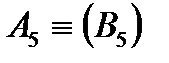розміститься від осі х₄₅ на відстані , що дорівнює відстані від проекцій А₁ та В₁ до осі х₁₄.

Спільне розв’язання першої і другої задач дозволяє знаходити:

а) відстань від точки до прямої;

б) відстань між двома паралельними прямими;

в) відстань між перехресними прямими.

На рис. 1.4.5 зображено розв’язання третьої та четвертої задач перетворення площини загального положення в проекціювальну та перетворення її в площину рівня. При цьому здійснено дві заміни площин проекцій.

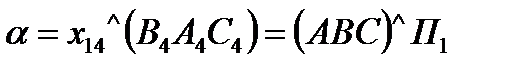
Рисунок 1.4.5

При першій заміні відсік площини (АВС) переведено в проекціювальне положення, а при другій заміні знайдено натуральну величину відсіку. Щоб перевести відсік у проекціювальне положення, необхідно в межах відсіку побудувати лінію рівня, бо для її перетворення в точку досить однієї заміни. На рисунку у відсіку проведено горизонталь АD, а нову вертикальну площину П₄ побудовано перпендикулярно до горизонтальної проекції горизонталі (А₁D₁). У системі площин проекцій 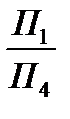площина АВС перетворилась у проекціювальну площину і на площині проекцій П₄ спроекціювалась у відрізок прямої В₄С₄. При другій заміні вісь х₄₅ проводять паралельно відрізку В₄С₄, а від осі х₄₅ відкладають відрізки, що дорівнюють відстані від точок горизонтальної проекції до осі х₁₄.

У системі площин проекцій площина АВС перетворилась у площину рівня і на площині проекцій П₅ спроекціювалась у натуральному вигляді А₅В₅С₅.

Спільне розв’язання третьої та четвертої задач дозволяє знаходити:

а) натуральні величини плоских фігур;

б) відстань від точки до площини;

в) кути нахилу площини до площини проекцій;

г) відстань між паралельними площинами.