Рішення транспортної задачі методом потенціалів

Початковий опорний план перевіряють на оптимальність за допомогою потенціалів. Відповідно кожному постачальнику А_і ставимо потенціал u_і, а кожному споживачеві В_j – v_j.

Критерій оптимальності опорного плану транспортної задачі: якщо для деякого опорного плану (х_іj) транспортної задачі існують такі числа-потенціали u_і і v_j, що для базисних клітинок виконуються рівності u_і+v_j=с_іj, а для небазисних - u_і+v_j ≤ с_іj для всіх 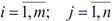, то такий опорний план є оптимальним.

Потенціали опорного плану визначаються з системи u_і+v_j=с_іj, які записують для всіх заповнених клітинок таблиці транспортної задачі. За допомогою розрахованих потенціалів перевіряють умову оптимальності u_і+v_j ≤ с_іj для незаповнених клітинок таблиці. Якщо хоча б для однієї небазисної клітинки ця умова не виконується, тобто u_і+v_j > с_іj, то поточний план не є оптимальним і переходимо до нового опорного плану.

Перехід від одного опорного плану до іншого виконують заповненням небазисної клітинки, для якої порушено умову оптимальності. Якщо таких клітинок кілька, то для заповнення вибирають таку, яка має найбільше порушення, тобто 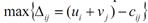. Для обраної порожньої клітинки будують цикл перерахунку.

Циклом в транспортній задачі називають замкнуту ламану лінію, сторони якої проходять уздовж рядків і стовпчиків таблиці, і одна з вершин якої знаходиться в небазисній клітинці, для якої порушено умову оптимальності, а всі інші вершини – базисні клітинки.

Перерозподіл продукції в межах циклу здійснюють за такими правилами:

а) кожній вершині циклу приписують певний знак, причому незаповненій клітинці знак "+", а всім іншим почергово "–" і "+";

б) у пусту клітинку заносять менше з чисел, що стоять у клітинках зі знаком "–". Одночасно це число прибавляють до відповідних чисел, що стоять у клітинках зі знаком "+" і віднімають від клітинок, що розміщені у клітинках зі знаком "–".

Отже, клітинка, яка була вільною, стала заповненою, а відповідна клітинка, де знаходилося найменше число (у вершині з "-") стала незаповненою. У результаті такого перерозподілу продукції ми отримаємо новий опорний план транспортної задачі, який знову перевіряємо на оптимальність. Якщо рішення оптимальне, то обчислюємо мінімальне значення цільової функції (мінімальну вартість перевезення всієї продукції), а якщо неоптимальне, то знову будуємо цикл перерахунку і за допомогою зсуву по циклу переходимо до нового опорного плану. Процес повторюють до тих пір, поки не буде отримано оптимальне рішення транспортної задачі. Значення базисних клітинок, які не брали участі в циклі перерахунку, в новій таблиці залишаються без змін. Можуть зустрітися такі види циклів:

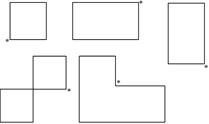
Приклад 2. Найти оптимальний план перевезень однорідного вантажу від постачальників А₁, А₂, А₃, А₄ із запасами а₁=90, а₂=85, а₃=125, а₄=І05 до споживачів В₁, В₂, В₃ з потребами у цьому вантажі b₁=110, b₂=155, b₃=140, який забезпечить мінімальну вартість перевезень вантажу, якщо відома вартість перевезень одиниці вантажу від постачальників до споживачів:

.

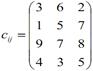Перевіримо, чи є транспортна задача закритою. Обрахуємо:

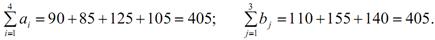
Так як 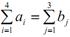, то транспортна задача закритого типу.

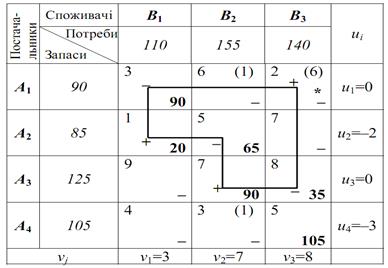
Побудуємо початковий опорний план транспортної задачі діагональним методом:

.

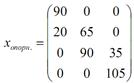Вартість перевезень за даним опорним планом буде складати: Z₁=3·90+1·20+5·65+7·90+8·35+5·105=270+20+325+630+280+525=2050 гр. од.

Перевіримо, чи є знайдений опорний план оптимальним. Для базисних клітинок мають виконуватися рівності u_і+v_j=с_іj:

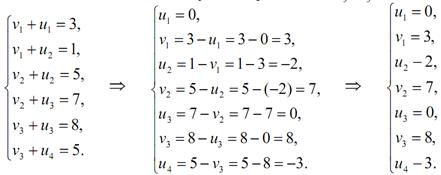
Ми маємо систему з 6 рівностей з 7 невідомими. Ця система має багато рішень. Візьмемо однин з невідомих, що дорівнює любому числу, наприклад, u₁=0, і знайдемо всі інші потенціали. Знайдені значення потенціалів запишемо до таблиці. Тепер виповнимо перевірку другої умови критерію оптимальності транспортної задачі, а саме: чи виконується для небазисних (незаповнених) кліток нерівності u_і+v_j ≤ с_іj.

Для клітинки (А₁В₂): v₂+u₁≤6; 7+0>6, отже нерівність не виконується;

Для клітинки (А₁В₃): v₃+u₁≤2; 8+0>2, отже нерівність не виконується;

Для клітинки (А₂В₃): v₃+u₂≤7; 8+(-2) ≤7, отже нерівність виконується;

Для клітинки (А₃В₁): v₁+u₃≤9; 3+0 ≤9, отже нерівність виконується;

Для клітинки (А₄В₁): v₁+u₄≤4; 3+(-3) ≤4, отже нерівність виконується;

Для клітинки (А₄В₂): v₂+u₄≤3; 7+(-3)>3, отже нерівність не виконується.

Маємо три клітинки (А₁В₂), (А₁В₃) та (А₄B₂), для яких не виконується нерівність u_і+v_j≤с_іj, а це означає, що опорний план не є оптимальним. У клітинках (А₁В₂), (А₁В₃) та (А₄B₂) у правому верхньому куті клітинки записуємо у скобках різницю між сумою потенціалів і вартістю перевезення одиниці вантажу окреслених клітинок та обираємо клітинку, для якої ця різниця є найбільшою, так обираємо клітинку (A₁B₃) і у ній ставимо зірочку (*). Для цієї клітинки будуємо цикл перерахунку на величину 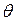= mіn (90; 65; 35) = 35, тобто до чисел, які знаходяться у позитивних вершинах, додаємо 35, а від чисел, що знаходяться у негативних вершинах, віднімаємо 35:

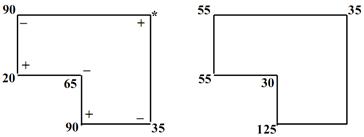
а) до перерахунку б) після перерахунку

Всі інші клітинки залишаємо без змін.

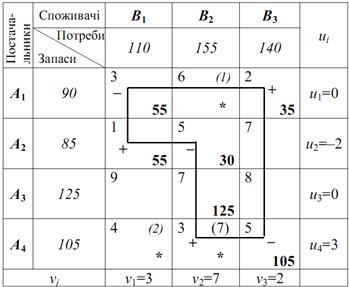
Отримано новий опорний план:

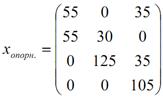
Вартість перевезень складе при даному плані:

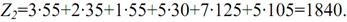
Перевіряємо план на оптимальність: знову записуємо систему рівнянь, знаходимо все потенціали, заносимо їх значення до таблиці і дивимося, чи виконуються нерівності u_і+v_j≤с_іj для небазисних клітинок:

v₂+u₁= 7 + 0 =7 >6 нерівність не виконується;

v₃+u ₂ = 2 – 2 = 0 <7;

v₁+u₃ = 3 + 0 = 3 <9

v₁+u₄ = 3 + 3 = 6 >4 нерівність не виконується;

v₂+u₄ = 7 + 3 = 10 >3 нерівність не виконується.

Таким чином, є ще три клітинки, а саме (A₁B₂), (A₄B₁) та (A₄B₂), для яких ці нерівності не виконуються. Будуємо цикл перерахунку на розмір Ө = mіn (55; 30; 105) = 30 для клітинок (A₄B₂), так як різниця між сумою потенціалів та вартістю перевезень вантажів для неї є найбільшою (дорівнює 7). Переходимо до наступної таблиці.

Новий опорний план:

Вартість перевезень становить при даному плані:

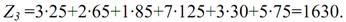
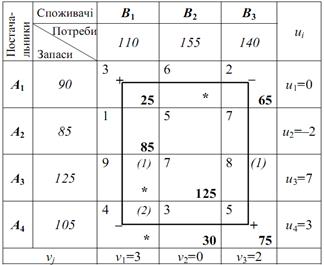
Ще є небазисні клітинки (A₃B₁), (A₃B₃) і (A₄B₁), для яких не виконуються нерівності u_і+v_j≤с_іj. Тому будуємо цикл перерахунку на величину Ө = mіn (25; 75) = 25 для клітинки (A₄B₁), так як різниця між сумою потенціалів та вартістю перевезень одиниці вантажу для неї дорівнює 2 (найбільша). Отримаємо таблицю:

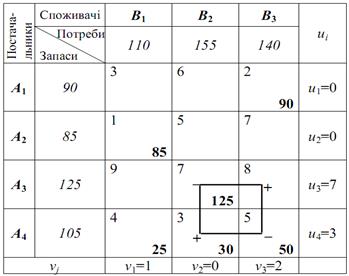
Новий опорний план:

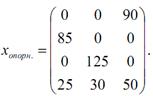
Загальна вартість перевезень складе:

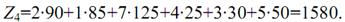
Так як у клітинці (А₃В₃) ще порушується друга умова критерію оптимальності транспортної задачі, а саме u₃+v₃>с₃₃ (7+2>9), то для цієї клітинки робимо цикл перерахунку на величину Ө = mіn (125; 50) = 50. У результаті отримаємо:

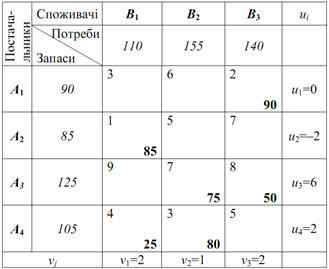
Знову обраховуємо всі потенціали та записуємо їх значення до таблиці. Для всіх небазисних клітинок останньої таблиці виконується нерівність u_і+v_j ≤ с_іj, а це означає, що отримано оптимальний план перевезення вантажу:

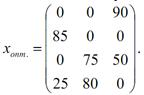
Мінімальна вартість перевезення вантажу складе:

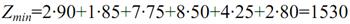гр. од.