Модель формування штатного розкладу фірми. Задача про призначення
4.1 Модель формування штатного розкладу фірми
Припустимо, що деяка фірма здійснює процедуру формування штатного розкладу. позначимо: j – індекс посад, 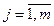 ,
, 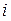 – індекс групи кандидатів на займані посади,
– індекс групи кандидатів на займані посади, 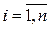 . Зараз фірма має n груп різних посад, у кожній з яких є bj вільних. Претенденти на вакансії проходять тестування, за результатами якого їх ділять на n груп по aі кандидатів у кожній. Для кожного кандидата з
. Зараз фірма має n груп різних посад, у кожній з яких є bj вільних. Претенденти на вакансії проходять тестування, за результатами якого їх ділять на n груп по aі кандидатів у кожній. Для кожного кандидата з 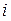 -тої групи необхідні певні витрати cіj на навчання для призначення його на j-ту посаду. Тут можливі випадки, коли кандидат повністю відповідає посаді, якщо cіj=0; кандидат зовсім не може займати посаду, якщо cіj = ∞.
-тої групи необхідні певні витрати cіj на навчання для призначення його на j-ту посаду. Тут можливі випадки, коли кандидат повністю відповідає посаді, якщо cіj=0; кандидат зовсім не може займати посаду, якщо cіj = ∞.
Ставиться завдання про оптимальний розподіл кандидатів на відповідні посади за умови мінімальних фінансових витрат на їх навчання.
Для знаходження оптимальної стратегії дій припустимо, що число претендентів відповідає числу запропонованих вакансій. У цьому випадку отримуємо транспортну задачу закритого типу. В іншому випадку маємо справу з транспортною задачею відкритого типу. Тут постачальником виступає група претендентів на вакансії, а в ролі споживача виступають групи вакантних посад. Витрати на навчання кандидатам cіj будуть служити тарифами на перевезення.
Невідомими величинами задачі будуть хіj – кількість кандидатів i-тої групи, які призначаються на j-ту посаду. З урахуванням введених позначень, економіко-математична модель задачі буде мати вигляд:
Знайти таке рішення хіj, яке забезпечить:
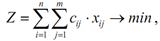
при виконанні умов:
1) всі кандидати на посади мають бути працевлаштованими:
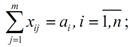
2) всі вакантні посади мають бути заповненими:
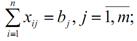
3) рівновага попиту та пропозиції:
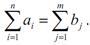
4.2 Задача про призначення
Розглянута задача є типовою задачею економіки праці, тому з її допомогою можна отримати відповіді на питання: «Як розподілити робітників по верстатах, щоб спільне вироблення було найбільшим або витрати на заробітну плату найменшими?», «Як призначити людей на різні посади?», «Як розподілити автомашини на маршрути / водіїв на машини / групи по аудиторіям / наукові теми по науково-дослідним лабораторіям?» і т.д.
У загальному вигляді закриту задачу про призначення можна сформулювати таким чином. Нехай є n робіт і n працівників – кандидатів для їх виконання. Кожному призначенню i-го працівника ( 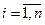 ) на j-ю роботу (
) на j-ю роботу ( 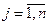 ) відповідає або певна кількісна ефективність (прибуток, продуктивність, якість робіт), або витрати будь-якого ресурсу (наприклад, час виконання робіт). Позначимо ці величини як сij. Потрібно знайти такі призначення працівників на всі роботи, які забезпечать найбільшу ефективність (або максимум сумарного позитивного ефекту, або мінімум сумарних витрат). За такого призначення необхідно враховувати, що кожного працівника можна призначити тільки на одну з робіт і кожна робота може виконуватися тільки одним працівником. Тобто ресурси неподільні між роботами, а роботи неподільні між ресурсами.
) відповідає або певна кількісна ефективність (прибуток, продуктивність, якість робіт), або витрати будь-якого ресурсу (наприклад, час виконання робіт). Позначимо ці величини як сij. Потрібно знайти такі призначення працівників на всі роботи, які забезпечать найбільшу ефективність (або максимум сумарного позитивного ефекту, або мінімум сумарних витрат). За такого призначення необхідно враховувати, що кожного працівника можна призначити тільки на одну з робіт і кожна робота може виконуватися тільки одним працівником. Тобто ресурси неподільні між роботами, а роботи неподільні між ресурсами.
Математична модель задачі має вигляд:
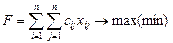 ,
,
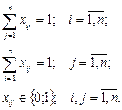
Якщо цільова функція буде прагнути до мінімуму, то дану задачу можна розглядати як окремий випадок транспортної задачі, де кожен працівник – постачальник з потужністю 1, а кожна робота – споживач з тією ж потужністю. При такому підході задачу про призначення можна вирішувати за допомогою алгоритмів розв’язання закритої (або відкритої) транспортної задачі.
Для знаходження оптимального варіанту розв’язання задачі про призначення вручну ефективним є так званий угорський метод.
Приклад. Фірма «Бетта» отримала замовлення на розробку п'яти програмних продуктів. Виконання замовлення було доручене п'яти найбільш досвідченим програмістам. Кожен з них повинен написати одну програму. Час виконання кожної роботи кожним з фахівців наведено в таблиці.
| Спеціаліст | Час виконання, дн. | ||||
| Програма 1 | Програма 2 | Програма 3 | Програма 4 | Програма 5 | |
| Рюмін | |||||
| Глухов | |||||
| Зайцев | |||||
| Коваленко | |||||
| Іванов |
Необхідно розподілити роботи між програмістами, щоб загальний час виконання заказу був мінімальним.
Рішення. Етап 1. У кожному рядку шукаємо мінімальний елемент (виділено жирним в таблиці) і віднімаємо від всіх елементів рядка. Отримаємо:
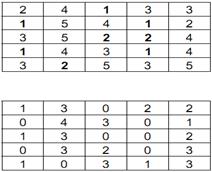
Тепер проводимо аналогічну процедуру для всіх стовпців: шукаємо найменший елемент по стовпцю і віднімаємо його з усіх елементів стовпця. Отримаємо:
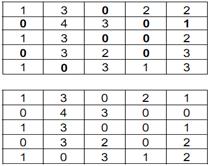
Етап 2. Вибираємо рядок з одним нулем (рядок №1), виділяємо нуль жирним і закреслюємо (виділено сірим) наявні нульові значення цього стовпця (стовпця №3).
Вибираємо рядок з одним нульовим значенням (рядок №5), виділяємо нуль.
Вибираємо рядок з одним нулем (рядок №3), виділяємо нуль жирним і закреслюємо (виділено сірим) наявні нульові значення цього стовпця (стовпця №4).
Вибираємо рядок з одним нулем (рядок №4), виділяємо нуль жирним і закреслюємо (виділено сірим) наявні нульові значення цього стовпця (стовпця №1).
Вибираємо рядок з одним нульовим значенням (рядок №2), виділяємо нуль.
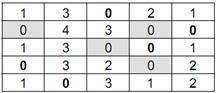
Отримаємо оптимальну матрицю призначень:
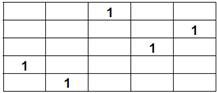
Мінімальне значення цільової функції складе: 1+2+2+1+2=8.
Алгоритм рішення задачі про призначення
Етап 1.
1. Формалізація проблеми у вигляді транспортної таблиці за аналогією з рішенням транспортної задачі.
2. У кожному рядку таблиці знайти найменший елемент і відняти його з усіх елементів цього рядка.
3. Повторити ту ж саму процедуру для стовпців.
Етап 2.
Якщо деяке рішення є допустимим, то кожному рядку і кожному стовпцю відповідає тільки один елемент.
1. Знайти рядок, що містить тільки одне нульове значення вартості, і в клітку, відповідну даному значенню, помістити один елемент. Якщо такі рядки відсутні, допустимо розпочати з будь-якого нульового значення вартості.
2. Закреслити інші нульові значення даного стовпця.
3. Пункти 1 і 2 повторювати до тих пір, поки продовження описаної процедури виявиться неможливим.
Якщо на даному етапі виявиться, що є кілька нулів, яким не відповідають призначення і які є незакреслені, то необхідно:
4. Знайти стовпець, що містить тільки одне нульове значення, і у відповідну клітку помістити один елемент.
5. Закреслити інші нулі в цьому рядку.
6. Повторювати пункти 4 і 5 до тих пір, поки подальша їх реалізація виявиться неможливою.
Якщо виявиться, що таблиця містить невраховані нулі, повторити операції 1-6. Якщо рішення є допустимим, тобто всі елементи розподілені в клітини, яким відповідає нульова вартість, то отримане рішення одночасно є оптимальним. Якщо рішення є неприпустимим, здійснюється перехід до третього етапу.
Етап 3.
1. Провести мінімальне число прямих через рядки і стовпці матриці (але не по діагоналях) таким чином, щоб вони проходили через всі нулі, що містяться в таблиці.
2. Знайти найменший серед елементів, через які не проходить жодна з проведених прямих.
3. Відняти його з усіх елементів, через які не проходять прямі.
4. Додати знайдений елемент до всіх елементів таблиці, які лежать на перетині проведених раніше прямих.
5. Всі елементи матриці, через які проходить лише одна пряма, залишити без зміни.
У результаті застосування даної процедури в таблиці з'являється принаймні один новий нуль. Необхідно повернутися до етапу 2 і повторювати алгоритм до тих пір, поки не буде отримано оптимальне рішення.
Приклад. Чотири верстатника можуть виконувати роботу на чотирьох верстатах. При цьому кожен з верстатників може працювати лише на одному верстаті. Продуктивність праці кожного верстатника задається матрицею:
Таблиця – Ефективність роботи верстатників
| Верстатники | I | II | III | IV |
| A | ||||
| B | ||||
| C | ||||
| D |
Як слід розподілити верстатників, щоб загальна продуктивність була максимальною?
Рішення.
Етап 1. Виходячи з того, що завдання вирішується на максимум, то елементи вихідної матриці множаться на (-1). У кожному рядку знаходиться найменший елемент. Найменший елемент віднімається з усіх елементів відповідного рядка.
У кожному стовпці знаходиться найменший елемент. Знайдений найменший елемент віднімається з усіх елементів відповідного стовпця. отримаємо:
Етап 2. Знайдене рішення є неприпустимим:
Етап 3. Проводимо найменше число прямих, що проходять через всі нулі таблиці.
 15 15
| |||
Найменшим елементом, через який не проходить жодна з прямих, є число 2. Скорегуємо таблицю так, як це описано вище відповідно до етапу 3, тобто віднімемо 2 з кожного елемента, через який не проходить жодна пряма, і додамо 2 до всіх елементів, що лежать на перетині двох прямих, залишивши без зміни всі інші елементи, через які проходить лише одна пряма. Тепер перерозподілимо відповідні призначення верстатників. отримаємо:
Знайдено таке рішення задачі:
Максимальна продуктивність праці складе: 47+40+58+83=228.
Питання для самоконтролю:
1. У чому зміст транспортної моделі, які її основні характеристики?
2. Охарактеризуйте зміст класичної транспортної моделі.
3. Які методи можуть бути використаними для розв’язання транспортної задачі?
4. У чому зміст та особливості використання методу найменшої вартості?
5. У чому зміст та особливості методу потенціалів?
6. Що таке модель формування штатного розкладу фірми?
7. Охарактеризуйте зміст та особливості використання задачі про призначення.
Рекомендована література:
основна: [1, 2, 4, 5, 6, 9];
додаткова: [3, 7, 8, 10-21].
Дата добавления: 2015-11-10; просмотров: 1087;
