Метод множників Лагранжа

Для розв’язання задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів і обчислювальних алгоритмів, які в основному ґрунтуються на теорії диференціального числення.

Оптимізаційні задачі, на змінні яких накладаються обмеження, вирішуються методами класичної математики. Оптимізацію з обмеженнями-рівностями можна виконати, наприклад, методом множників Лагранжа.

Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:

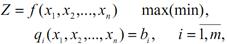
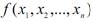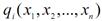де та – диференційовані.

Ідея методу Лагранжа полягає в заміні даної задачі більш простою – знаходження екстремуму більш складної функції, але без обмежень. Ця функція називається функцією Лагранжа і записується у вигляді:

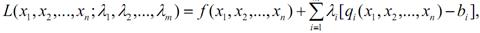
де 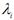– невизначені поки що величини, так звані множники Лагранжа.

Необхідною умовою екстремуму функції багатьох змінних є рівність нулю приватних похідних щодо всіх змінних функції. Обчислимо ці приватні похідні і прирівняємо їх до нуля:

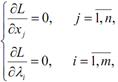
або

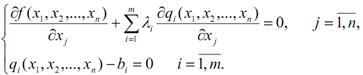
Вирішивши систему рівнянь, знайдемо 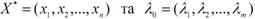– стаціонарні точки. Оскільки вони знайдені з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є точкою перегибу графіка функції.

Теорема. Нехай навкруги критичної точки (x₀; y₀) функція F (x, y) має безперервні приватні похідні до другого порядку включно.

Складемо матрицю такого виду:

Обчислимо 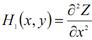та визначник матриці Н(х, у):

Якщо 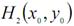>0, то у точці (х₀, у₀) досліджувана функція має екстремум.

Якщо при цьому 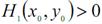, то у заданій точці функція досягає мінімального значення; якщо 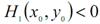, то – максимального значення.