Практичне застосування методу множників Лагранжа

Розглянемо економічний зміст множників Лагранжа. Для цього розглянемо задачу нелінійного програмування з визначення оптимального плану виробництва продукції при обмежених ресурсах:

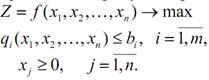
Головною метою виробництва продукції є отримання найбільшого прибутку від її реалізації, тому цільовою функцією Z завдання є прибуток від реалізації продукції обсягом Х=(х₁, х₂,...,х_n) одиниць. При цьому функція f(х₁, х₂,...х_n) – нелінійна.

Запишемо систему обмежень

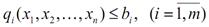
у вигляді

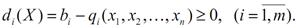
Якщо 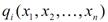– обсяг сировини і-го виду, який використовується для виробництва всієї продукції, то d_і(X) – залишок цього ресурсу після її виробництва. Якщо d_і(X)=0, то сировину використано повністю; якщо d_і(X)>0, то на виробництво продукції використано не всю сировину; якщо d_і(X) <0, то наявної сировини не вистачить на виробництво продукції.

Розглянемо функцію Лагранжа для даної задачі:

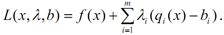
Отже, 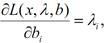тобто ця похідна показує, як змінюється значення цільової функції залежно від обмежень. Множники Лагранжа є подвійними змінними задачі про використання ресурсів. Вони можуть бути ціною, за яку на ринку продається або купується одиниця і-го виду сировини. Якщо 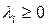і d_і(X)>0, то можна продати залишки сировини і отримати додатковий прибуток у розмірі 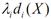. Якщо ж d_і(X)<0, то можна купувати потрібну кількість, витратив 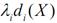грошових одиниць і забезпечити виробництво продукції обсягом Х=(х₁, х₂,...,х_n). Функцію Лагранжа можна трактувати як загальний прибуток від виробництва, який містить прибуток від реалізації виготовленої продукції f (x) і прибуток від продажу залишків сировини (або витрати на придбання потрібної кількості сировини) .

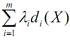Приклад. Фірма планує витратити 20000 грн. на рекламу. Одна хвилина реклами на телебаченні коштує 1000 грн., а на радіо – 500 грн. Аналітики фірми прогнозують збільшення приросту доходу фірми від використання рекламних засобів за функцією:

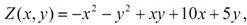
де Z(x,y) – приріст доходу фірми (тис. грн.) від реклами;

х – тривалість (хв.) рекламного ролика на телебаченні;

y – тривалість (хв.) рекламного ролика на радіо.

Яким чином потрібно з'єднати рекламу на телебаченні і радіо, щоб отримати максимальне значення приросту доходу фірми, економно використавши при цьому наявні грошові кошти на рекламу?

Рішення. Цільова функція – це максимум приросту доходу фірми.

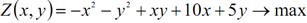
при виконанні таких умов:

а) за наявністю грошових коштів на рекламу:

1000 x + 500 y = 20000;

б) відносно невід’ємності змінних: .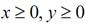

Оптимальне рішення знаходимо за допомогою методу множників Лагранжа.

Функція Лагранжа набуває вигляду:

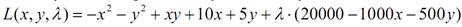
Приватні похідні прирівнюємо до нуля:

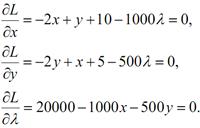
Отримаємо систему рівнянь:

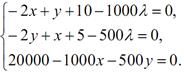
Зробимо відповідні перетворення:

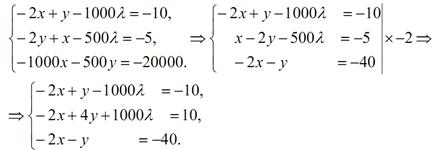
Складемо перші рівняння останньої системи та отримаємо:

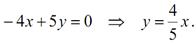
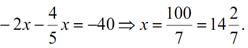
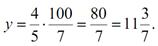
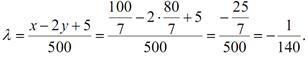
Рішення систему рівнянь: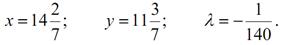

Переконаємося, чи досягає наша функція екстремального значення в знайденій точці. Для цього на основі вищезгаданої теореми знайдемо приватні похідні першого порядку заданої функції:

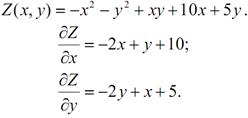
Знайдемо приватні похідні другого порядку:

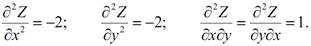
Отже

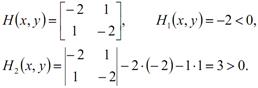
Згідно з умовою теореми стверджуємо, що точка з координатами 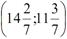буде точкою максимуму функції. Максимальне значення функції:

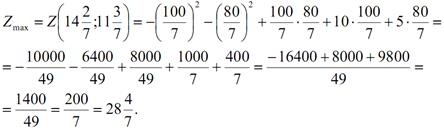
Фірма отримає додатковий дохід від використання реклами у розмірі 28 4/7 тис. грн. якщо гроші, призначені на рекламу, будуть використані на 14 2/7 хв. реклами на телебаченні та 11 3/7 хв. – на радіо.

Питання для самоконтролю:

1. Які задачі відносяться до задач нелінійного програмування?

2. Охарактеризуйте економічну сутність методу множників Логранжа.

3. Наведіть практичні аспекти застосування методу множників Логранжа.

Рекомендована література:

основна: [1, 2, 4, 5, 6, 9];

додаткова: [3, 7, 8, 10-21].

СПИСОК ЛІТЕРАТУРИ

1. Баранкевич М.М., Антонів В.Б. Вступ до математичної економіки. Фундаментальні моделі. – Дрогобич: Коло, 2009. – 348 с.

2. Бахрушин В.Є. Математичне моделювання: Навч. посіб. – Запоріжжя: ГУ «ЗІДМУ», 2004. – 140 с.

3. Башун М.Економіко-математичне моделювання процесу управління запасами підприємства // Схід. – №2. – 2008. – С.43-45.

4. Економіко-математичне моделювання: Навч. посіб. / За ред. О.Т. Іващука. – Тернопіль: ТНЕУ «Економічна думка», 2008. – 704 с.

5. Економіко-математичне моделювання: Навч. посіб. / За заг. ред. В.В. Вітлінського. – К.: КНЕУ, 2008. – 536 с.

6. Економіко-математичне моделювання: Навч. посіб. / За ред. О. Т. Іващука. – Тернопіль: ТНЕУ «Економічна думка», 2008. – 704 с.

7. Жильцов О.Б. Математичне програмування (з елементами інформаційних технологій): Навч. посіб. для студ. вищ. навч. закл. / О.Б. Жильцов, В.Р. Кулян, О.О. Юнькова; За ред. О.О. Юнькової. – К.: МАУП, 2006. – 184 с.

8. Казарєзов А.Я., Ципліцька О.О. Економіко-математичне моделювання: Навч. посіб. для самостійного вивчення. – Миколаїв: Вид-во ЧДУ ім. Петра Могили, 2009. – 248 с.

9. Кундышева Е.С. Экономико-математическое моделирование: Учебник для вузов / под ред. Б.А. Суслакова. – М.: Изд.-торг. корпорация «Дашков и К», 2010. – 424с.

10. Лугінін О.Є. Економетрія: Навч. посіб. – К.: Центр учбової літератури, 2008. – 278 с.

11. Мамонов К.А. Економіко-математичне моделювання. – Харків: ХНАМГ, 2009. – 86 с.

12. Невежин В.П., Кружилов С.И. Сборник задач по курсу «Экономико-математическое моделирование». – М.: ОАО «Издательский дом «Городец», 2005. – 320 с.

13. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – М.: Вузовский учебник, 2005. – 144 с.

14. Пелих А.С. Экономико-математические методы и модели в управлении производством / А.С. Пелих, Л.Л. Терехов, Л.А. Терехова. – Ростов н/Д: «Феникс», 2005. – 248 с.

15. Стеценко І.В. Моделювання систем: навч. посіб. / І.В. Стеценко; М-во освіти і науки України, Черкас. держ. технол. ун-т. – Черкаси: ЧДТУ, 2010. – 399 с.

16. Стеценко І.В., Бойко О.В. Система імітаційного моделювання засобами сіток Петрі // Математичні машини і системи. – К., 2009. – №1. – С.117-124.

17. Федосеев В.В. Математическое моделирование в экономике и социологии труда. Методы, модели, задачи. – М.: ЮНИТИ-ДАНА, 2007. – 167 с.

18. Шелобаев С.И. Экономико-математические методы и модели: Учеб. пособ. для вузов. – М.: ЮНИТИ-ДАНА, 2005. – 287 с.

19. Экономико-математические методы и прикладные модели: Учеб. пособ. для вузов / Под ред. В.В. Федосеева. – М.: ЮНИТИ-ДАНА, 2002. – 391 с.

20. Kelton W.D., R.P. Sadowski, and D.A. Sadowski: Simulation with Arena, McGraw-Hill, New York (1998).

21. Systems Modeling Corporation: Arena User’s Guide, Version 4.0, Sewickly, Pennsylvania (1999).