Аналіз біомедичних сигналів на основі методу власних векторів

Одним з поширених підходів при аналізі сигналів і розпізнаванні образів є ортогональне перетворення в координатний базис власних векторів коваріаційної матриці, отриманої для ансамблю ЕКГ сигналів. Методика розкладу ансамблю ЕКГ в базисі власних векторів дозволяє розділити аналізований кардіосигнал на підпростір сигналу і підпростір шуму. В основі методу лежить аналіз власних значень і власних векторів кореляційної матриці, яка визначається для ансамблю реалізацій сигналу. Власні вектори, що відповідають K найбільшим власним значенням, утворюють базис в підпросторі сигналу. Решта N-K власних векторів утворюють базис підпростору шуму.

Якщо в інтервалі часу T₁ < t < T₂, що відповідає одному повному циклу виникнення та поширення збудження в серці, через рівні проміжки провести вибірку значень х_i(t), то i-й кардіоцикл у векторному вигляді представляється як X_i = [X_i(t₁) X_i(t₂) ... X_i(t_N)] = [x_i1 x_i2 ... x_iN], де N — кількість дискретних значень сигналу, t₁ ≤ t₂≤ ... ≤ t_N. Тоді ансамбль реалізацій M послідовних кардіоциклів матиме вигляд матриці

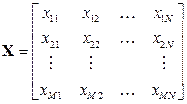, (9.20)

де x_ij — j-е дискретне значення i-ї реалізації.

Рис. 9.18. Поділ ЕКГ на підпростір сигналу і підпростір шуму

Досліджуваний кардіосигнал представляється у новому координатному базисі за допомогою розкладу за системою ортогональних функцій. Для даних цілей застосовують розклад Карунена-Лоєва та сингулярний розклад.

Коваріаційна матриця ансамблю ЕКГ з M реалізацій має вигляд

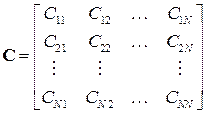, (9.21)

де елементи C_ij матриці С задаються наступним чином:

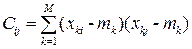, (9.22)

де m_k — середнє значення, що розраховується для k-ї реалізації за формулою

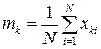. (9.23)

Для власних векторів V₁, V₂, …, V_N коваріаційної матриціС, які представляють собою ортонормований базис ансамблю ЕКГ, виконується умова

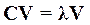, (9.24)

де λ₁, λ₂, …, λ_N — власні значення, причому λ₁> λ₂> …> λ_N (рис. 9.19).

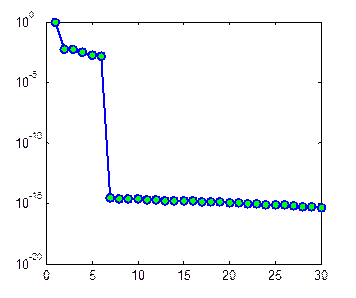
Рис. 9.19. Розподіл власних значень λ_i / λ_max (перші 30 значень)

В отриманому базисі головні власні вектори (рис. 9.20), які відповідають найбільшим власним значенням λ₁ > λ₂ >…> λ_K, містять основну інформацію про сигнал.

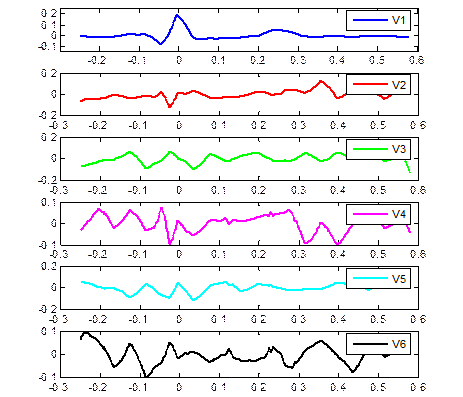
Рис. 9.20. Головні власні вектори 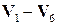ансамбля ЕКГ

Коефіцієнти розкладу (проекції) в базисі головних власних векторів 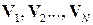отримують у результаті скалярного добутку обраної реалізації ЕКГ на відповідні координатні вісі

(9.25)

Відновлення в координатному базисі головних власних векторів виконується відповідно до виразу

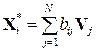. (9.26)

Похибка відновлення сигналу залежить від кількості власних векторів, які відкидаються при відновленні. При аналізі ЕКГ сигналів достатньо врахувати від 3 до 6 головних власних векторів та власних значень, які їм відповідають (рис. 9.21).

Рис. 9.21. Початковий ЕКГ сигнал та відновлений після розкладу в базисі власних векторів по 3 і 6 головним власним векторам