Вейвлет-перетворення

Обмеженням спектрального методу аналізу є неможливість визначення точної локалізації конкретної частотної складової кардіосигналу в часі, що є принципово важливим для ранньої діагностики порушень електрофізіологічних властивостей міокарда. На відміну від перетворення Фур'є, вейвлет-перетворення забезпечує двовимірну розгортку, при цьому, масштаб і координата розглядаються як незалежні змінні, що дає можливість аналізу сигналів відразу в двох просторах ─ масштабному і часовому. Результати вейвлет-аналізу біомедичного сигналу містять не тільки інформацію про розподіл енергії сигналу за частотними складовими, але і відомості про часові координати, на яких виявляються ті чи інші частотні складові, або на яких відбуваються швидкі зміни частотних складових сигналу, як, наприклад, у разі наявності пізніх потенціалів передсердь чи шлуночків у ЕКГ.

Вейвлет-перетворення є багаторівневим аналізом, ефективним для дослідження сигналів, що містять високочастотні компоненти короткої тривалості і довготривалі низькочастотні компоненти. Дана особливість підходить для задачі виявлення низькоамплітудних високочастотних складових біомедичних сигналів та їх аналізу незалежно від високоамплітудних низькочастотних складових.

Розрізняють неперервне і дискретне вейвлет-перетворення. Обидва підходи мають свої переваги під час аналізу біомедичних сигналів.

Неперервне вейвлет-перетворення (НВП) визначається як:

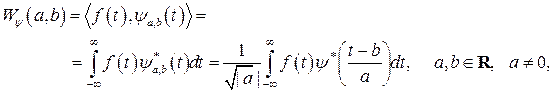(9.16)

де <> ─ оператор скалярного добутку;

* ─ оператор комплексного спряження;

ψ_{a, b} ─ двопараметричне сімейство функцій:

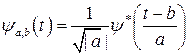, (9.17)

де b ─ параметр, який визначає зсув вздовж вісі часу t;

a ─ масштабний коефіцієнт, який відповідає за розтягування і стиснення материнської вейвлет-функції ψ (t).

Таким чином, набір вейвлет-функцій є набором масштабованих (розтягнутих або стиснутих, в залежності від значення параметра a) і зміщених (в залежності від значення параметра 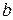) копій єдиного прототипу ─ материнської породжуючої функції 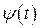. Материнські вейвлет-функції являють собою функції, що обмежені за часом і місцем розташування на часовій вісі і мають спектральний образ, певною мірою локалізований на частотній вісі. Вимоги до материнських вейвлет-функцій визначаються можливістю відновлення вихідного сигналу 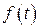за його вейвлет-спектром .

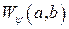Реконструкція сигналу виконується за формулою оберненого неперервного вейвлет-перетворення:

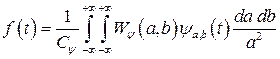, (9.18)

де С_ψ ─ константа, що залежить від обраного вейвлета.

Коефіцієнти неперервного вейвлет-перетворення містять інформацію про енергію окремих компонент біомедичного сигналу і про час їх появи. Це дозволяє одночасно досліджувати повільну і швидку динаміку змін сигналів у часі, а також виявляти діагностично важливі локальні особливості, наприклад, наявність ППП у ЕКГ (рис. 9.15).

Головною перевагою використання вейвлетів є можливість локального аналізу. Вейвлет-аналіз здатен розкрити такі аспекти даних, які не виявляються іншими методами аналізу сигналів, наприклад, точки розриву у сигналі, різкі нелінійності у вищих гармоніках та самоподібність. За допомогою вейвлет-аналізу також можна проводити стиснення та знешумлення сигналу без помітного зниження амплітуди.

Дискретне вейвлет-перетворення оперує з дискретними значеннями масштабного коефіцієнта a і параметра зсуву b, які задаються, як правило, у вигляді степеневих функцій, що дозволяє уникнути надлишкової кількості операцій і розрахованих коефіцієнтів, характерних для НВП.

При багаторівневому дискретному вейвлет-розкладі (ДВР) біомедичного сигналу визначаються коефіцієнти апроксимації сA, які представляють згладжений сигнал для контурного аналізу сигналу, і коефіцієнти деталізації cD, що описують високочастотні флуктуації сигналу. Для аналізу біомедичного сигналу на різних масштабах використовуються деревовидно з'єднані фільтри нижніх і верхніх частот з різними частотами зрізу. Вектори вейвлет-коефіцієнтів отримують за допомогою математичної операції згортки сигналу S, що досліджується, з фільтром нижніх частот для визначення коефіцієнтів апроксимації сА₁ і з фільтром верхніх частот для визначення коефіцієнтів деталізації сD₁. На наступному кроці розкладаються коефіцієнти апроксимації сА₁ на дві частини, з одержанням сА₂ та сD₂ і т.д. до необхідного рівня розкладання N (рис. 9.16).

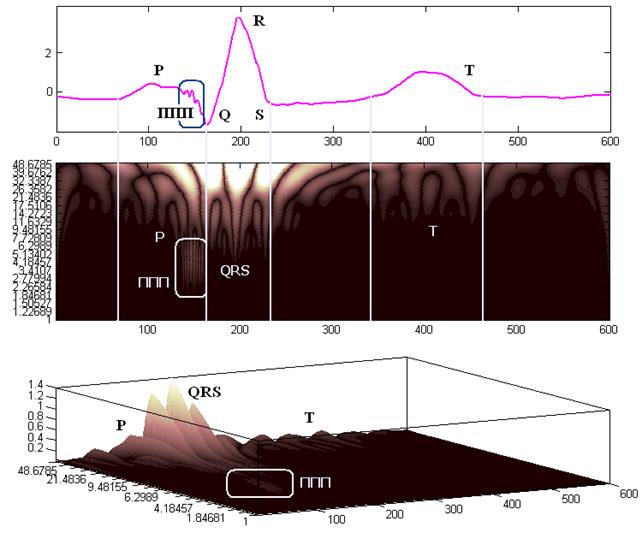
Рис. 9.15. Аналіз ЕКГ за допомогою НВП:

а) кардіоцикл з наявністю змодельованих ППП в термінальній частині Р зубця; б) двовимірна скейлограма НВП; в) тривимірна скейлограма НВП

Рис. 9.16. Дерево дискретного вейвлет-розкладання сигналу S до рівня N

Таким чином, в процесі відновлення сигнал S представляють як суму апроксимуючої складової, яка визначається за коефіцієнтами апроксимації N-го рівня вейвлет-розкладання (a_N) і всіх деталізуючих складових, що визначаються за коефіцієнтами деталізації рівнів ДВР з 1 по N (d_N, d_N-1, ... d₁) (рис. 9.17):

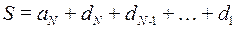. (9.19)

Видалення шуму, компресія і згладжування ЕКГ сигналів за допомогою вейвлет-перетвореннябазуються на тому, щобагаторівневе вейвлет-розкладання кардіосигналу дозволяє відокремити вейвлет-коефіцієнти, що відповідають за шумові складові, і відновити сигнал без завад.

Рис. 9.17. Дискретне вейвлет-розкладання ЕКГ сигналу до 3 рівня

Шумові складові таких біомедичних сигналів, як ЕКГ, відображаються головним чином в деталізуючих коефіцієнтах вейвлет-розкладання, тому при видаленні шуму зазвичай обробляють ці коефіцієнти. Найпростіший спосіб видалення шуму полягає в тому, щоб зробити нульовими значення коефіцієнтів, що менші за деяке порогове значення. Ця процедура називається порогової обробкою (трешолдінгом) коефіцієнтів. Широкого поширення набули такі методи порогової обробки, як жорсткий трешолдінг і м'який трешолдінг.

Під час жорсткої порогової обробки зберігаються незмінними всі коефіцієнти, що більші за значення порога τ або дорівнюють йому за абсолютною величиною, а коефіцієнти менші за значення τ обнуляються. Під час м'якої порогової обробки разом з перетворенням в нуль коефіцієнтів, по модулю менших, ніж τ, відбувається зменшення по модулю решти коефіцієнтів на величину τ.

Для вирішення задачі зниження шумів у ЕКГ сигналі необхідно: оцінити спектральний склад шумової компоненти, вибрати тип порогової обробки (трешолдінга) і критерій розрахунку самого порога. Від вибору порогового рівня фону (оцінки дисперсії шуму) залежить якість зниження шуму у сигналі, що оцінюється у вигляді відношення сигнал/шум. Завдання малих значень порогу τ зберігає шумовий фон в коефіцієнтах деталізації і призводить лише до незначного збільшення відношення сигнал/шум. При великих значеннях порогу τ можна втратити коефіцієнти, які несуть суттєву діагностичну інформацію. Пошук оптимального значення τ₀ означає знаходження такого порогу, який при найменшому спотворенні корисного відновленого сигналу забезпечує найбільше значення відношення сигнал/шум.

Якість зниження шумів у біомедичному сигналі (підвищення відношення сигнал / шум) залежить також від способу застосування трешолдінга. Використовують наступні способи порогової обробки:

• загальний трешолдінг, що здійснюється з використанням фіксованого значення порогу τ, єдиного для всіх рівнів і коефіцієнтів деталізації ЕКГ сигналу;

• багаторівневий трешолдінг, що здійснюється з використанням порогу τ, значення якого змінюються від рівня до рівня;

• локальний трешолдінг, що здійснюється з використанням порогу τ, який відрізняється не тільки на різних рівнях розкладання, але також залежить від позиції коефіцієнтів деталізації на даному рівні.