Постановка транспортної задачі

Транспортні моделі (задачі) – спеціальний клас задач лінійного програмування, які часто описують переміщення певного продукту. Призначення транспортної задачі – визначення обсягів перевезень з пунктів виробництва або зберігання до пунктів споживання з мінімальними сумарними витратами. У транспортній моделі передбачається, що вартість перевезення прямо пропорційна обсягу перевезеного продукту.

У загальному випадку транспортну модель можна застосовувати для опису ситуацій, пов'язаних з управлінням запасами, управлінням рухом капіталів, складанням розкладів, призначенням персоналу і т.д.

Класична модель транспортної задачі формулюється наступним чином: є m відправників А₁, А₂, ..., А_m (постачальники), у яких зосереджено відповідно а₁, а₂, ..., а_m одиниць однорідної продукції. Цю продукцію слід доставити в n пунктів споживання В₁, В₂, ..., В_n (споживачі), попит яких відповідно дорівнює b₁, b₂, ..., b_n одиниць.

Відома вартість перевезення одиниці вантажу c_ij від кожного i-го постачальника j-му споживачеві 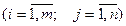. Потрібно скласти план перевезень, тобто вказати такі значення х_ij 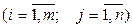- кількість вантажу, що перевозиться від постачальника А_i до споживача B_j, при яких загальна вартість перевезень буде мінімальною.

Передбачається, що споживачам все одно, від яких пунктів виробництва (постачальників) постачається продукція, аби її обсяг був відповідним.

Математичне формулювання поставленого завдання має наступний вигляд.

Цільова функція – загальна вартість всіх перевезень повинна бути мінімальною:

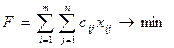(1)

При обмеженнях:

- всі запаси мають бути вивезеними:

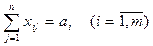; (2)

- всі потреби мають бути задоволеними:

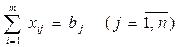; (3)

При граничних умовах:

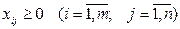(4)

У моделі (1)-(4) обумовлюється, що

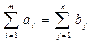, (5)

тобто сума пропозиції і попиту збігається. Така задача називається закритою або збалансованою.

В іншому випадку мають справу з відкритою задачею. При цьому для розв’язання транспортної задачі її зводять до закритого типу наступним чином:

1) якщо пропозиція перевищує попит 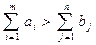, то вводиться «фіктивний споживач» В_ф, якому приписується фіктивна заявка:

.

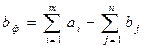Вартість перевезень від усіх постачальників до фіктивного споживача приймається рівною нулю, тобто .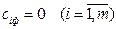

Отримане в результаті рішення задачі значення х_ij буде означати, що у постачальника А_i залишилося не затребуваним х_ij одиниць продукції.

2) якщо пропозиція менше попиту 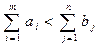, то вводиться «фіктивний постачальник» А_ф, якому приписується фіктивний запас:

.

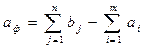Вартість перевезень від фіктивного постачальника до всіх споживачів приймається рівною нулю, тобто 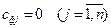. Отримане у результаті рішення задачі значення покаже, що заявка споживача В_j залишається не задоволеною на х_ij одиниць продукції.

До методів розв’язання транспортної задачі відносяться:

а) спеціальні методи розв’язання транспортної задачі;

б) симплексний метод.

Транспортна задача є задачею лінійного програмування, яку можна розв’язати симплексним методом, однак при цьому виходять симплекс-таблиці великих розмірів. Тому для реалізації даного завдання ручним способом (при невеликій кількості постачальників і споживачів) застосовуються спеціальні методи.

Як і при розв’язанні задачі симплексним методом, рішення транспортної задачі спеціальними методами складається із знаходження опорного і оптимального рішення. Для знаходження опорного рішення найбільш часто використовуються методи: (діагональний) північно-західного кута і мінімального елемента. Для знаходження оптимального рішення розроблено розподільний метод, модифікований симплекс-метод (метод МОДІ), метод потенціалів, угорський метод і ряд ін.

Побудова початкового опорного плану

2.1 Метод північно-західного кута

Розглянемо алгоритм побудови початкового опорного плану транспортної задачі методом північно-західного кута:

1. Перевірка транспортної задачі на закритість. Якщо вона відкрита, то приводимо її до задачі закритого типу.

2. Першою заповнюємо верхню ліву клітинку. Заповнення клітинки A_іB_j таблиці здійснюється за правилами:

а) якщо а_і<b_j, тобто запаси менше потреб, то в цю клітину записуємо весь обсяг запасу продукції а_і, перераховуємо потребу споживача B_j, постачальника A_і виключаємо з розгляду (наприклад, проставив у всіх клітинках рядка, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки A_і+1B_j;

б) якщо а_і>b_j, тобто запаси більше потреб, то у цю клітинку записуємо весь обсяг потреби у продукції b_j, перераховуємо запаси постачальника A_і, виключаємо з розгляду споживача B_j (ставимо у всіх клітинках стовпчика, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки A_іB_j+1;

в) якщо а_і=b_j, тобто запаси дорівнюють потребам, то у цю клітинку записуємо весь обсяг потреб або запасів, виключаємо із розгляду постачальника A_і та споживача B_j (ставимо у всіх клітинках стовпчика та рядка, крім заповнених, прочерки) и переходимо до заповнення наступної клітинки A_і+1B_j+1.

3. Серед незаповнених клітинок (без обсягу продукції і прочерків) знову вибираємо верхню ліву клітинку таблиці і заповнюємо її за правилами, описаним у п. 2. Так продовжуємо до тих пір, поки не заповнимо всі клітинки таблиці.

4. З отриманої таблиці виписуємо початковий опорний план транспортної задачі і обчислюємо значення цільової функції при цьому плані.

Приклад 1. Методом північно-західного кута (діагональним) знайти початковий опорний план перевезення однорідної продукції від постачальників А₁, А₂, A₃ із запасами а₁=200, a₂=150, а₃=175 до споживачів В₁, B₂, В₃, В₄ із потребами в цій продукції b₁=140, b₂=125, b₃=90, b₄=170, якщо відома вартість перевезень одиниці продукції від постачальників до споживачів:

.

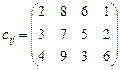Рішення.

Перевіримо, чи являється транспортна задача закритою. Вичислимо:

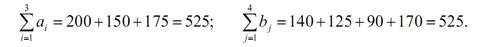
Так як 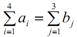, то задача є закритого типу. Отримано таку таблицю:

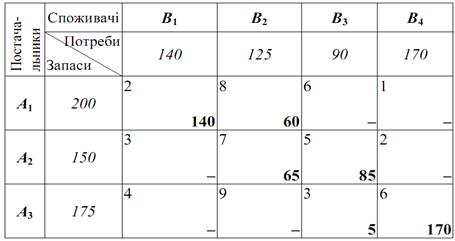
Начальний опорний план має вид:

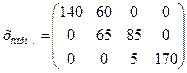Щоб дізнатися, якою буде вартість перевезення продукції за таким планом, потрібно перемножити вартість перевезення одиниці продукції на обсяг, який перевозиться, для всіх заповнених (де немає прочерків) клітинок таблиці і знайти їх суму, а саме:Z = 2·140+8·60+7·65+5·85+3·5+6·170=280+480+455+425+15+1020=2675.

2.2 Метод найменшої вартості

Правила знаходження початкового опорного плану транспортної задачі методом найменшої вартості відрізняються від правил знаходження такого плану діагональним методом тільки послідовністю вибору клітинки, яку потрібно заповнювати. Згідно з методом найменшої вартості, першою вибирається клітинка з найменшою вартістю перевезення одиниці вантажу від постачальника до споживача. Якщо таких клітинок кілька, то вибираємо ту, для якої кількість продукції, яку можна перевезти, найбільша.

Алгоритм методу найменшої вартості побудови початкового опорного плану транспортної задачі розглянемо на попередньому прикладі 1.

Отримана наступна підсумкова таблиця:

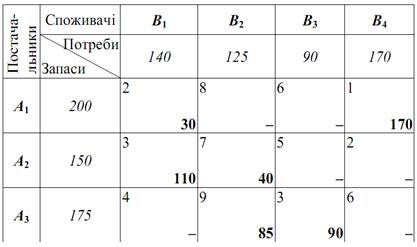
Начальний опорний план має вид:

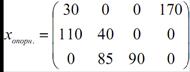
Сумарна вартість перевезень всієї продукції при цьому складе:

Z = 2·30+1·170+3·110+7·40+9·85+3·90=60+170+330+280+765+270=1875.

Після побудови начального опорного плану кожним з методів у таблиці має бути заповнено (m+n-1) клітинок, де m – кількість постачальників, n – кількість споживачів. Заповнені клітинки називаються базисними, а незаповнені – вільними (небазисними).

Для того щоб з’ясувати, який метод знаходження початкового опорного плану транспортної задачі є найбільш ефективним, порівняємо загальну вартість перевезення за опорними планами, знайденими кожним з методів. Бачимо, що найменша вартість отримана за допомогою методу найменшої вартості (Z=1875). Значно більшу вартість перевезень (Z=2675) всієї продукції дає діагональний метод побудови начального опорного плану. Тобто, найбільш ефективним методом побудови начального опорного плану транспортної задачі є метод найменшої вартості.