Элементы дисперсионного анализа

Дисперсионный анализ является одним из методов изучения влияния одного или нескольких факторных признаков на результативный признак. В зависимости от количества факторов дисперсионный анализ подразделяется на однофакторный и многофакторный. Ниже рассмотрено применение дисперсионного анализа для случая однофакторного комплекса.

В основе дисперсионного анализа лежит расчленение общей вариации изучаемого признака по источникам ее происхождения на два вида вариации:

• систематическую вариацию, которая обусловлена изменением признака-фактора;

• остаточную (случайную) вариацию, обусловленную действием прочих, случайных, не связанных с данным фактором обстоятельств.

Для разграничения этих вариаций всю совокупность наблюдавшихся единиц разбивают на группы (классы) по факторному признаку и исчисляют средние результативного признака по группам.

Групповые средние

;

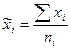общая средняя

.

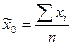где x_i - индивидуальные значения признака в группе;

n_i - число единиц, входящих в группу;

п - общее число наблюдений.

Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием признака-фактора.

Для ответа на поставленный вопрос определяют два показателя дисперсии:

1) показатель 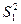, характеризующий колеблемость групповых
средних вокруг общей средней (межгрупповая дисперсия);

2) показатель 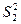, отражающий остаточную, внутригрупповую
дисперсию. Полученные показатели сравнивают, получая фактическое дисперсионное отношение:

.

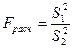При дисперсионном анализе межгрупповую 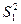и внутригрупповую 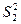дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы:

;

,

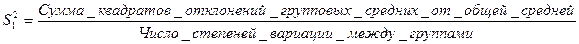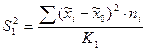где 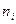— число единиц в группе:

;

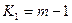т - число групповых средних (число выделенных групп по признаку-фактору);

.

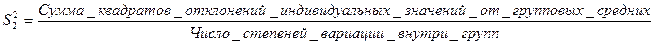
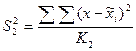По таблице F-распределения Р. Фишера (см. приложение 5) при определенном уровне значимости (или доверительной вероятности)¹ и числе степеней свободы (К₁ и К₂) определяется табличное дисперсионное отношение (F_табл).

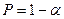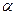¹ Доверительная вероятность , где - уровень значимости.

Если F_расч >Ft_табл , то следует считать, что гипотеза о влиянии признака-фактора не опровергается.