Расслоенная (типическая или районированная) выборка

В составе генеральной совокупности с различным уровнем изучаемого признака желательно обеспечить более равномерное представительство в выборочной совокупности различных типов. Эта цель достигается при применении расслоенной (типической или стратифицированной) выборки. Эту выборку применяют также в целях более равномерного представления в выборке различных районов, и в этом случае ее называют районированной выборкой.

При типической выборке неоднородная генеральная совокупность подразделяется на более однородные в отношении изучаемых признаков группы (типы, районы). По каждой группе определяются ее объем ( 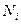) и число подлежащих наблюдению единиц ( 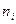). Отбор обследуемых единиц производится в каждой группе при помощи одного из способов случайного отбора - повторного или бесповторного.

Общее число единиц выборочной совокупности распределяется между группами пропорционально численности групп в составе генеральной совокупности. Такой отбор называется пропорциональным.

N — общая численность единиц в генеральной совокупности

,

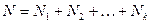где N₁, N₂, ..., N_k - численность отдельных групп генеральной совокупности;

п — общий объем выборочной совокупности.

Объем выборки для каждой группы –

;

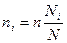где 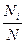- удельный вес данной (i - й) группы в генеральной совокупности;

n = n₁+n₂+…+n_k.

Кроме пропорционального размещения по группам численности единиц выборочной совокупности применяется так называемое оптимальное размещение, при котором число наблюдений в группе определяется по формуле

.

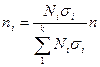Формулы для расчета ошибок типической выборки приведены в табл. 4.3.

В табл. 4.3 приняты следующие условные обозначения:

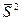- средняя групповая выборочная дисперсия средней;

;

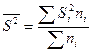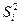— внутригрупповая дисперсия данной (i-и) группы в выборочной совокупности;

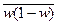- средняя групповая выборочная дисперсия доли;

;

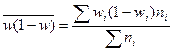Как видно из приведенных формул, величина стандартной ошибки типической выборки зависит только от точности определения групповых средних, т. е. от величины внутригрупповых дисперсий. Согласно правилу сложения дисперсий общая дисперсия слагается из межгрупповой дисперсии и средней из внутригрупповых дисперсий. Отсюда следует, что ошибка типической случайной выборки меньше, чем ошибка простой случайной выборки.

Предельная (максимально возможная) ошибка типической выборки:

;

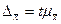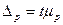
Таблица.3

Формулы ошибок типической выборки

	Способ отбора единиц
повторный	бесповторный
Средняя ошибка ( 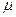): для средней: а) при пропорциональном размещении единиц
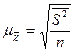
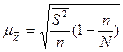
б) при оптимальном размещении единиц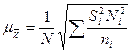
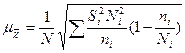
для доли: а) при пропорциональном размещении единиц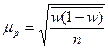
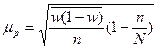
б) при оптимальном размещении единиц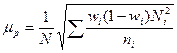

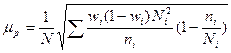
Необходимый объем выборки определяется на основе формулы и величины допустимой ошибки.

Серийная выборка

Сущность серийной выборки заключается в том, что вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение. Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производиться в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.

Стандартная ошибка при равновеликих сериях определяется по формулам, представленным в табл. 4.

Таблица 4

	Способ отбора серий
повторный	бесповторный
Средняя ошибка ( 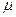): для средней
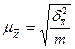
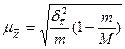
для доли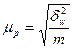

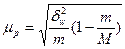
В табл. 4.4 приняты следующие условные обозначения:

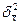— межгрупповая выборочная дисперсия средней;

;

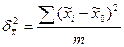где 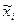- средний уровень признака в серии;

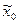- средний уровень признака для всей выборочной совокупности;

т - число равных серий в выборочной совокупности;

М - число равных серий в генеральной совокупности;

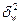- межгрупповая выборочная дисперсия доли;

,

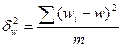где w_i - доля единиц, обладающих данным признаком в серии;

w — доля единиц, обладающих данным признаком во всей выборочной совокупности.

Ошибка серийной выборки больше, чем при любом другом способе отбора. Тем не менее серийный отбор широко применяется на практике, что объясняется его организационными преимуществами.