Отображения и функции

Пусть заданы два множества А и В. Если для каждого элемента 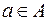указан элемент 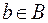, с которым сопоставляется а, то говорят, что между множествами А и В установлено соответствие.

Соответствие называется функциональным, если образом любого элемента из множества А является единственный элемент из множества В. График такого соответствия называется функциональным. Это означает, что в нем нет пар с одинаковыми первыми и различными вторыми компонентами.

Функциональное соответствие называется функцией.

Отображением называют всюду определенную функцию. Отображением множества А в множество В (функцией на А со значениями в В) называется правило, по которому каждому элементу множества А сопоставляется элемент множества В.

Т.к. понятие «функция» шире понятия «отображение», то в дальнейшем употребляется «функция».

Способы задания функций:

1 Аналитический. Аналитическим выражением называется символическое обозначение совокупности математических операций, которые производятся в определенной последовательности. Если 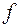обозначает аналитическое выражение, то функция задана аналитически, например 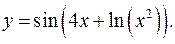Функция может иметь разные аналитические выражения на разных подмножествах множества Х, например: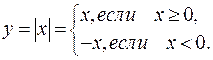

2 Табличный. Функция определена таблицей своих значений или конечными списками пар.

Например:

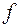
	x
y

В этом случае вычисление значений функции сводится к непосредственному считыванию соответствующих пар. Если необходимо знать значение функции для аргументов, отсутствующих в таблице, то его можно приблизительно вычислить при помощи правил интерполяции или экстраполяции.

3 Графический. Этот способ заключается в графическом изображении пар в выбранной системе координат.

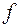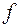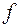4 Алгоритмический, типичным примером которого является рекурсивный способ. Рекурсивные процедуры задают функции следующим образом: заранее определено значение функции для одного или нескольких «начальных» значений аргумента, например (0) или (0) и (1). Значения функции при других аргументах определяются через ее значения в предыдущих точках. Как правило, рекурсивные процедуры задаются на множестве (подмножестве) натуральных чисел N. Например, функция n!: 1!=1; (m+1)!=m!(m+1). По определению 0!=1. Отличительной особенностью такого значения функции является то, что при вычислении значения функции для аргумента x=m, требуется предварительно вычислить значение функции во всех предыдущих точках. Для m! – это значения функции в точках 1, 2, 3, ..., m-1.

Т.к. в функциональной зависимости каждый элемент множества А связан с единственным элементом В, то в графических терминах функция описывается таким графом, у которого из каждой вершины, изображающей элементы множества А, выходит ровно одна стрелка.