Замыкания отношений

Если отношение на множестве M не обладает тем или иным свойством, то его можно попытаться продолжить до отношения R^*, которое будет им обладать. Для этого необходимо присоединить некоторые упорядоченные пары к подмножеству 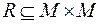. Исходное множество R будет подмножеством в R^*. В случае, если вновь построенное множество R^* будет минимальным среди всех расширений R с выделенным свойством, то оно будет являться замыканием R относительно данного свойства.

Пример 7. Пусть A 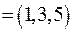. Отношение R на A задано упорядоченными парами: R 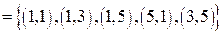. Отношение не рефлексивно, не симметрично и не транзитивно. Найдите соответствующие замыкания.

Замыкание относительно рефлексивности должно содержать все пары вида (a,a). Поэтому искомое замыкание имеет вид: R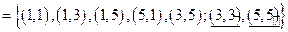^* (добавленные пары отделены подчеркиванием).

В отношение R^* добавлены пары (3,3) и (5,5); пара (1,1) уже была в отношении R. Теперь имеются все пары вида (a,a): (1,1), (3,3), (5,5). Получено рефлексивное замыкание.

Замыкание по симметричности должно содержать все пары, симметричные исходным. Построение замыкания целесообразно свести в таблицу.

Таблица 2

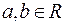
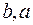
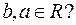
№ п/п				Примечание
	1,3	3,1	нет	Добавить пару (3,1) в отношение R
	1,5	5,1	да	–
	3,5	5,3	нет	Добавить пару (5,3) в отношение R

Как видно из таблице 2 в отношение R следует добавить две пары (3,1) и (5,3).

Замыкание по симметричности будет иметь вид R^* .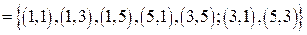

Чтобы выполнить замыкание по транзитивности, необходимо выполнить несколько шагов.

На первом этапе составляется таблица 3.

Таблица 3

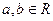
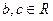
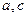
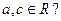
№ п/п					Примечание
	5,1	1,3	5,3	нет	добавить пару (5,3) в отношение R
	3,5	5,1	3,1	нет	добавить пару (3,1) в отношение R
	5,1	1,5	5,5	нет	добавить пару (5,5) в отношение R

Из анализа таблицы видно, что следует добавить пары (5,3), (3,1), (5,5) в отношение R. Полученное замыкание имеет вид: .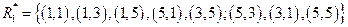

Второй этап. Из анализа 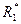видно, что возникло сочетание пар (3,1) и (1,3), поэтому отношение R^* должно содержать пару (3,3). Следовательно, .

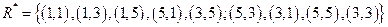Теперь все необходимые пары добавлены. Метод, приведенный выше, достаточно трудоемок и состоит в переборе практически всех пар.

Можно познакомиться с методом построения замыкания по транзитивности по матрице достижимости ориентированного графа. (учебная дисциплина «Теория вероятностей и математическая статистика»).

Замыкание по транзитивности имеет много приложений. Допустим, задан ориентированный граф, отражающий коммуникационную сеть. В этом случае замыкание по транзитивности позволяет определить, существует ли возможность переправить сообщение из одного места в другое.

Отношение эквивалентности и разбиение множества на классы.Бинарное отношение R называется отношением эквивалентности, если оно одновременно обладает тремя свойствами: рефлексивностью, симметричностью и транзитивностью.

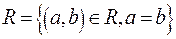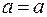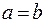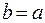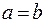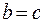Например, отношение равенства является отношением эквивалентности. Действительно, пусть M –произвольное множество. Введем бинарное отношение . Т.к. для всякого a, то R рефлексивно. Так как из равенства следует, что для всех a и b, то R симметрично. Так как из того, что и следует, что 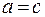для любых a, b, c, то R транзитивно.

Без доказательства приводятся еще некоторые примеры отношения эквивалентности: отношение «имеет тот же возраст» на множестве всех людей; «имеет один и тот же остаток при делении на 3» на множестве натуральных чисел. Можно привести и другие примеры. Все они наводят на мысль, что если на множестве задано отношение эквивалентности, то все его элементы можно разбить на непересекающиеся подмножества. Все элементы в любом из таких подмножеств эквивалентны друг другу.

Разбиением множества Aназывается совокупность непустых подмножеств A₁, A₂, …, A_n множества A, удовлетворяющая следующим требованиям:

1)

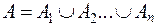
2)

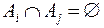
Таким образом, отношение эквивалентности разбивает множество на непересекающиеся подмножества, которые называются классами эквивалентности.

Диаграмма Венна разбиения множества A на пять блоков (подмножеств) показана на рис.9.

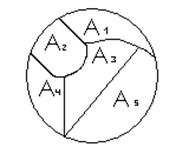
Рис.9

Подмножества изображены не заходящими одно на другое, т.к. они не могут иметь общих элементов. Множество классов эквивалентности множества A называется фактор - множеством.