Пример 8.
Рис.10
Пример 9. Определите, какие из следующих отношений между множествами
A={a, b, c}и B={1, 2,3}являются функциями из множества А в В.
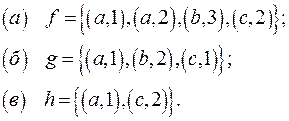
Решение:
(а) Отношение 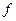 – не функция, поскольку элементу а соответствуют два разных элемента множества В: 1 и 2.
– не функция, поскольку элементу а соответствуют два разных элемента множества В: 1 и 2.
(б) Отношение g является функцией.
(в) Последнее отношение функцией не является, поскольку элементу b не соответствует ни одного элемента.
Пример 10. Какие из отношений являются функциями?
(а) «х – брат или сестра у» на множестве всех людей;
(б) отношение на множестве Z, задано парами: 
(в) отношение на множестве R, задано парами: 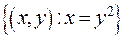
Решение:
(а) Это не функция, поскольку есть люди с несколькими братьями и сестрами, а также бывают семьи с единственным ребенком, т.е. ни брата, ни сестры нет.
(б) Отношение б функция, поскольку по каждому числу х его квадрата х2 определяется однозначно.
(в) Последнее отношение – не функция, так как, например, обе упорядоченные пары: 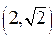 и
и 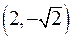 - ему принадлежат. Кроме того, в нем отсутствуют пары (х, у) с отрицанием х.
- ему принадлежат. Кроме того, в нем отсутствуют пары (х, у) с отрицанием х.
Пусть 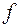 – функция из множества А в множество В. Поскольку для каждого
– функция из множества А в множество В. Поскольку для каждого 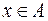 существует единственным образом определенный
существует единственным образом определенный 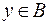 , такой, что
, такой, что 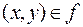 , мы будем писать у =
, мы будем писать у = 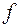 (х), и говорить, что функция
(х), и говорить, что функция 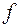 отображает множество А в множество В, а
отображает множество А в множество В, а 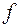 (х) называть образом х при отображении
(х) называть образом х при отображении 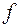 или значением
или значением 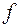 , соответствующим аргументу х.
, соответствующим аргументу х.
Кроме того, можно написать 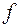 :A→B, чтобы подчеркнуть, что функция
:A→B, чтобы подчеркнуть, что функция 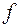 переводит элементы из А в элементы В. Множество А принято называть областью определения, а В – областью значений функции
переводит элементы из А в элементы В. Множество А принято называть областью определения, а В – областью значений функции 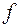 .
.
Типы отображений.Отображение называется ее инъективным или инъекцией, или взаимно однозначным отображением, иначе «в», если 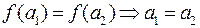 для всех
для всех 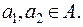 .
.
Это определение логически эквивалентно тому, что 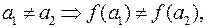
т.е. у инъективной функции нет повторяющихся значений. Иными словами, разные входные данные дают различные выходные данные.
Будем называться функцию 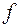 сюръективной или сюръекцией, или функцией «на», если множество ее значений совпадает с областью значений. Это означает, что для каждого
сюръективной или сюръекцией, или функцией «на», если множество ее значений совпадает с областью значений. Это означает, что для каждого 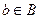 найдется такой
найдется такой 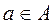 , что b=
, что b= 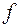 (a). Таким образом, каждый элемент области значений является образом какого – то элемента из области определения
(a). Таким образом, каждый элемент области значений является образом какого – то элемента из области определения 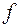 .
.
Мы называем 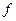 биективной функцией или просто биекцией, если она как инъективна, так и сюръективна.
биективной функцией или просто биекцией, если она как инъективна, так и сюръективна.
Пример 11. Определите, какие из функций, изображенных на рис. 11, инъективны, а какие сюръективны. Перечислите все биекции.
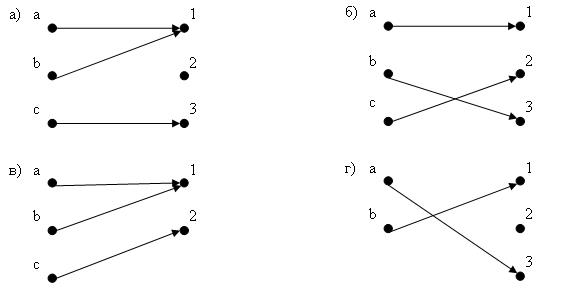
Рис.11
Решение:
(а) Данная функция не инъективна, поскольку значение 1 соответствует как a, так и b. Она не является и сюръекцией, ввиду того, что в элемент 2 ничего не переходит.
(б) Данная функция инъективна, т.к. не имеет повторяющихся значений. Она же и сюръективна, поскольку множество ее значений совпадает со своей областью значений.
(в) Значение 1 эта функция принимает как на а, так и на b. Следовательно, она не инъективна. Однако данная функция сюръективна, поскольку в ее множество значений входят все элементы области значений.
(г) Последняя функция инъективна, но не сюръективна (в элемент 2 ничего не переходит).
Только в случае (б) мы имеем биекцию.
Обратные функции. Пусть  - произвольная функция. Рассмотрим функцию
- произвольная функция. Рассмотрим функцию 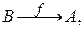 закон которой задан следующим образом:
закон которой задан следующим образом: 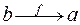 в том и только в том случае, если
в том и только в том случае, если 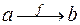 . Построенная таким образом функция называется обратнойк функции
. Построенная таким образом функция называется обратнойк функции 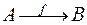 . При графическом представлении обратная функция получается из данной переменной направления стрелок.
. При графическом представлении обратная функция получается из данной переменной направления стрелок.
Если функция задана аналитически, например, у = 5х и требуется найти обратную, то следует:
1) выразить х через у;
2) переименовать переменные.
В соответствии с заданной функцией: 1) 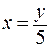
2) 
Таким образом, обратная функция будет 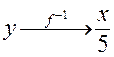 .
.
Если функция задана перечислением пар, например, 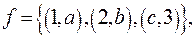 то для задания обратной функции следует пометь местами образы и прообразы, т.е.
то для задания обратной функции следует пометь местами образы и прообразы, т.е. 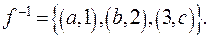
Обратными для тригонометрических функций являются: для sin x - arcsin x,
для cos x – arcos x и т.д.
Для логарифмических функций обратной будет показательная и наоборот. Обратной для х2 будет 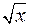 и т.д.
и т.д.
Обратная функция 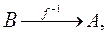 однозначна в том и только в том случае, когда заданная функция
однозначна в том и только в том случае, когда заданная функция 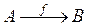 инъективна.
инъективна.
Функция 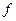 обратима только тогда, когда она биективна.
обратима только тогда, когда она биективна.
Суперпозиция функций.Результатом суперпозиции двух данных функций 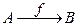 и
и 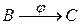 называется функция
называется функция 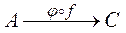 , закон которой
, закон которой  задается следующим образом:
задается следующим образом: 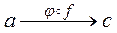 в том и только в том случае, если существует такой элемент
в том и только в том случае, если существует такой элемент 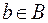 , что
, что 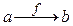 и
и  .
.
Функция 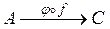 , полученная таким способом из функций
, полученная таким способом из функций 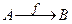 и
и 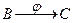 называется их композицией.
называется их композицией.
Пример 12. Даны две функции  и
и  (рис.12).
(рис.12).
 | |||||||||
|
|
| |||||||
|
|
|
|
| |
 |  | ||||||
 |  | ||||||
Рис.12
В функции 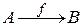
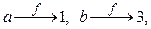
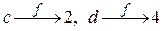 в функции
в функции 
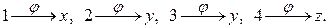
В соответствии с определением получаем, что в новой функции 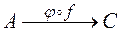
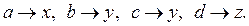
Пример 13. Заданы функции 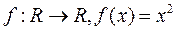 и
и 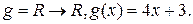 Вычислить
Вычислить 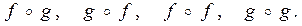
Решение. Все четыре новые функции определены на R со значениями в R.
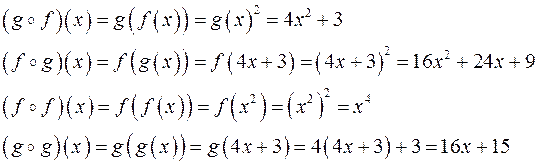
Как видно из вычислений, результат суперпозиции двух данных функций зависит от их порядка, т.е. операция суперпозиции не обладает свойством коммутативности.
В современных языках программирования функции используется очень широко. Они дают нам возможность выделить отдельные вычисления в подпрограммы. В большинстве языков есть специальные библиотеки с наиболее часто применяющимися функциями, такими как sin x, log x, 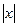 и т.д. Кроме того, в них легко создавать собственные функции.
и т.д. Кроме того, в них легко создавать собственные функции.
В некоторых особенно мощных языках, известных как языки функционального программирования, основные операторы определены в терминах функций. Главная особенность таких языков – возможность построения новых, более сложных, операторов из основных. Чтобы уметь это делать, нам необходимо в совершенстве овладеть композицией функций.
Дата добавления: 2015-08-21; просмотров: 3381;
