Основные определения. Алгоритмом называется точное предписание, определяющее вычислительный процесс, который ведет от варьируемых исходных данных к искомому результату

Алгоритмом называется точное предписание, определяющее вычислительный процесс, который ведет от варьируемых исходных данных к искомому результату, т.е. алгоритм – это совокупность правил, определяющих данный вычислительный процесс.

Для каждого алгоритма существует некоторая совокупность возможных исходных данных — объектов, к которым имеет смысл применять рассматриваемый алгоритм. Для каждого алгоритма выделяется область применимости: если процесс применения алгоритма к какому-либо объекту заканчивается выдачей результатов, то говорят, что он применим к этому объекту.

Алгоритм задает функцию, определенную на его области применимо­сти и ставящую в соответствие каждому элементу этой области результат применения к нему алгоритма.

Не все объекты, встречающиеся в математике, могут служить исходными данными, результатами или промежуточными данными алгоритма.

В алгоритмических процессах могут участвовать лишь конструктив­ные объекты.

Конструктивными объектамибудем называть натуральные и рациональные числа, полиномы с натуральными или рациональными коэффициентами, матрицы с натуральными или рациональными элементами, слова в некотором алфавите и т. д., т. е. такие объекты, которые могут быть построены целиком и представлены для рассмотрения.

Поскольку возможными исходными данными и результатами алгоритма могут быть лишь конструктивные объекты, то лишь конструктивные объекты могут быть аргументами и значениями вычислимой функции.

По классическому определению буква– это графический знак, который сам по себе или в сочетании с другими знаками используется для обозначения на письме звуков, фонем, их основных вариантов и их типичных последовательностей. По А.А. Маркову «буквами называются знаки, которые в данном их применении рассматриваются только как целые. В этом смысле типограф или знаки являются буквами (при чтении книги нас не интересуют части знаков, например Y состоит из 2-х частей u и j, а лишь целые знаки). Буква – понятие условное, его объем зависит от принятых соглашений. Например, нижеприведенные знаки рассматриваются как буквы, т.е. как нерасчленяемые целые: ы, 2, !, =, ≤ . Т.е. буквами можно считать любые заранее оговоренные, имеющие достаточную ясную форму знаки. Такие знаки, как 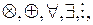|| и т.д. можно считать буквами.

Конечный набор букв можно считать алфавитом. Желательно, чтобы буквы, входящие в алфавит, различались по форме. Практически применяемый алфавит должен содержать не очень большое число букв, т.к. могут появиться похожие знаки.

Настоящий буквенный алфавит впервые появился у древних греков. Всего в мире насчитывается около двухсот алфавитов.

Слово – это ряд написанных друг за другом букв. Слово в данном алфавите – это слово, каждая буква которого принадлежит данному алфавиту. Очень важное требование состоит в единственности разложения слова на буквы данного алфавита – требование невозможности разночтений. Невозможность разночтений может быть достигнута наложением надлежащих ограничений на рассматриваемые алфавиты и на способы написания слов в них.

Можно, например, выставить два следующих требования:

а) всякая буква алфавита должна быть связной, т.е. должна изображаться без отрыва карандаша от бумаги.

б) при написании слов следует оставлять промежуток между всякими двумя соседними буквами

Первое из этих требований налагает ограничение на рассматриваемые алфавиты, а второе – на способ написания слов. Ясно, что при соблюдении этих требований всякое слово в рассматриваемом алфавите будет разлагаться на буквы единственным образом. Перечисленные выше условия являются достаточными, но отнюдь не необходимыми для единственности чтения слов. Так, несмотря на то, что русский печатный алфавит из-за несвязной буквы «ы» не удовлетворяет первому условию, разложение слов в этом алфавите на буквы, однозначно.

Пустым словом называется слово, не содержащее ни одной буквы и обозначаемое символом Λ.

Примеры.

1) 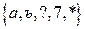- алфавит; 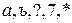- буквы.

2) 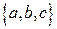- алфавит; 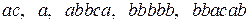- слова этого алфавита.

Основная операция на словах – операция приписывания слова к слову: если дано слово, имеющее вид 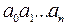, и слово вида 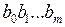, то можно образовать новое слово 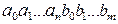, полученное приписыванием или соединением слов.

Если Λ – пустое слово, а 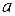- слово, то .

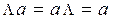Свойства алгоритмов.Анализ известных в математике алгоритмов дал возможность выявить характерные его свойства.

Свойство 1.Дискретность. Алгоритм описывает процесс последова­тельного построения величин, идущий в дискретном времени. Необходимый для вычисления интервал времени разбит на малые отрезки — такты. Система величин в конце каждого такта получается в результате осуществления элементарного шага алгоритма (определенной програм­мы преобразования) из системы величин, имеющейся к началу такта.

Свойство 2.Детерминированность (определенность ) требуется, чтобы метод действия (вычисления) был настолько точен и общепонятен, чтобы не оставалось места произволу. Этот метод можно сообщить другому лицу в виде конечного числа указаний, т.е. программа преобразований в каждом такте однозначно определена.

Свойство 3.Результативность. Это свойство, называемое иногда еще направленностью алгоритма, требует, чтобы алгоритмическая процедура, примененная к любой задаче данного типа, через конечное число шагов останавливалась и после остановки можно было бы прочесть искомый результат.

Свойство 4.Массовость. Алгоритм служит не для решения какой – либо одной конкретной задачи, а для решения целого класса задач. Процедуру для решения одной индивидуальной задачи не называют алгоритмом.

Свойство 5.Элементарность шагов алгоритма. Закон получения последующей системы величин из предшествующей должен быть простым.

Литература

1. Акимов О.Е. Дискретная математика. Логика, группы, графы. – М.: Лаборатория базовых знаний, 2003г.

2. Андерсон, Джеймс А. Дискретная математика и комбинаторика. – М.: Вильямс, 2004г.

3. Аматова Г.Е., Аматов М.А. Математика. – М.: Академия педагогических и социальных наук, 2008г.

4. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика.- Харьков.: Торсинг, 2003г.

5. Бочкарева О.В. Учебное пособие по математике (специальные главы) М.: Радио и связь, 2001г.

6. Болтянский В.Г., Славин А.П. Беседы о математике. Книга1. Дискретные объекты. – М.: ФИМА, МЦНМО, 2002г.

7. Воронов М.В., Мещерякова Г.П. – Математика. Ростов н/Д.: Феникс, 2002г.

8. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: Физматлит, 2005г

9. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. – М.: ФОРУМ – ИНФРА – М.: 2007г.

10. Ерусалимский Я.М. Дискретная математика. М.: Вузовская книга, 2003г.

11. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. – М.: Лаборатория базовых знаний, 2001г.

12. Лавров И.А., Максимов Л.Л. Задачи по теории множеств, математической логики и теории алгоритмов. – М.: Физматлит, 2001г.

13. Лексаченко В.А. Логика, множества, вероятность. – М.: Вузовская книга, 2001г.

14. Малаховский В.С. Числа знакомые и незнакомые. - Калининград.: ФГУИПП. Янтарный сказ, 2004г.

15. Москинова Г.И. Дискретная математика. – М.: Колос, 2000г.

16. Новиков Ф.А. Дискретная математика для программистов. – СПБ.: Питер, 2001г.

17. Романовский И.В. Дискретный анализ. – М.: Физматлит, СПБ: Невский диалект, 2001г.

18. Спирина М.С., Спирин П.А. Дискретная математика. – М.: Академия. 2004г.

19. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА – М, Новосибирск: НГТУ, 2002г.

20. Хаггарти Р. Дискретная математика для программистов. – М.: Техносфера, 2003г.

21. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПБ: БХВ – Петербург, 2005г.

22. Шиханович Ю.А. Введение в математику. – М.: Научный мир, 2005г.

23. Яблонский С.В. Введение в дискретную математику. М.: Высшая школа. 2003г.