Кванторы
Функциональная природа предиката влечет за собой введение ещё одного понятия – квантора. (quantum – от лат. «сколько») Кванторные операции можно рассматривать как обобщение операций конъюнкции и дизъюнкции в случае конечных и бесконечных областей.
Квантор общности 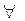 (все, всякий, каждый, любой (all – «всякий»)). Соответствующие ему словесное выражение звучит так:
(все, всякий, каждый, любой (all – «всякий»)). Соответствующие ему словесное выражение звучит так:
«Для всякого x Р(x) истинно». Вхождение переменной в формулу может быть связанным, если переменная расположена либо непосредственно после знака квантора, либо в области действия квантора, после которого стоит переменная. Все прочие вхождения – свободные, переход от P(x) к 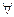 x(Px) или
x(Px) или 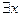 (Px) называется связыванием переменной x или навешиванием квантора на переменную x (или на предикат P) или квантификацией переменной х. Переменная, на которую навешивается квантор, называется связанной, несвязанная квантования переменная называется свободной.
(Px) называется связыванием переменной x или навешиванием квантора на переменную x (или на предикат P) или квантификацией переменной х. Переменная, на которую навешивается квантор, называется связанной, несвязанная квантования переменная называется свободной.
Например, переменная x в предикате Р(x) называется свободной ( x – любое из М), в высказывании 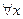 Р(x) переменную x называют связанной переменной.
Р(x) переменную x называют связанной переменной.
Справедлива равносильность 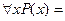 P(x1)
P(x1) 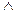 P(x2)
P(x2) 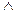 …
… 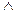 P(xn),
P(xn),
P(x) – предикат, определенный на множестве М={х1,х2...х4}
Квантор существования 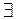 (exist – «существовать»). Словесное выражение, соответствующее ему, звучит так: “Существует x, при котором Р(x) истинно”. Высказывание
(exist – «существовать»). Словесное выражение, соответствующее ему, звучит так: “Существует x, при котором Р(x) истинно”. Высказывание 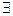 xР(x) уже не зависит от x, переменная x связана квантором
xР(x) уже не зависит от x, переменная x связана квантором 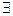 .
.
Справедлива равносильность:
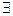 xP(x) = P(x1)
xP(x) = P(x1) 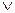 P(x2)
P(x2) 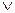 …
… 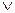 P(xn), где
P(xn), где
P(x) - предикат, определенный на множестве М={x1,x2…xn}.
Квантор общности и квантор существования называют двойственными, иногда используется обозначение квантора 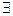 ! – «существует, и притом, только один».
! – «существует, и притом, только один».
Ясно, что высказывание 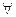 xP(x) истинно только в том единственном случае, когда Р(x) - тождественно истинный предикат, а высказывание
xP(x) истинно только в том единственном случае, когда Р(x) - тождественно истинный предикат, а высказывание 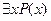 ложно только тогда, когда Р(x) - тождественно ложный предикат.
ложно только тогда, когда Р(x) - тождественно ложный предикат.
Кванторные операции применяются и к многоместным предикатам. Применение кванторной операции к предикату P(x,y) по переменной x ставит в соответствие двухместному предикату P(x,y) одноместный предикат 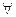 xP(x,y) или
xP(x,y) или 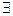 xP(x,y), зависящий от у и не зависящий от х.
xP(x,y), зависящий от у и не зависящий от х.
К двухместному предикату можно применить кванторные операции по обеим переменным. Тогда получим восемь высказываний:
1. 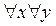 P(x,y); 2.
P(x,y); 2. 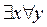 P(x,y);
P(x,y);
3. 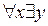 P(x,y); 4.
P(x,y); 4. 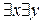 P(x,y);
P(x,y);
5. 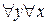 P(x,y); 6.
P(x,y); 6. 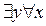 P(x,y);
P(x,y);
7. 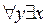 P(x,y); 8.
P(x,y); 8. 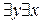 P(x,y)
P(x,y)
Пример 3. Рассмотреть возможные варианты навешивания кванторов на предикат P(x,y) – “x делится на y”, определенный на множестве натуральных чисел (без нуля) N. Дать словесные формулировки полученных высказываний и определить их истинность.
Операция навешивания кванторов приводит к следующим формулам:
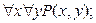
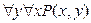 - высказывания “для любых двух натуральных чисел имеет место делимость одного на другое” (или 1) все натуральные числа делятся на любое натуральное число; 2) любое натуральное число является делителем для любого натурального числа) ложные;
- высказывания “для любых двух натуральных чисел имеет место делимость одного на другое” (или 1) все натуральные числа делятся на любое натуральное число; 2) любое натуральное число является делителем для любого натурального числа) ложные;
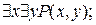
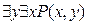 - высказывания “существуют такие два натуральных числа, что первое делится на второе” (1. «существует такое натуральное число x, которое делится на какое-то число y»; 2. «существует такое натуральное число y, которое является делителем какого-то натурального числа x») истинны;
- высказывания “существуют такие два натуральных числа, что первое делится на второе” (1. «существует такое натуральное число x, которое делится на какое-то число y»; 2. «существует такое натуральное число y, которое является делителем какого-то натурального числа x») истинны;
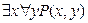 - высказывание “существует натуральное число, которое делится на любое натуральное”, ложное;
- высказывание “существует натуральное число, которое делится на любое натуральное”, ложное;
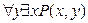 - высказывание “для всякого натурального числа найдется такое натуральное, которое делится на первое” (или для всякого натурального числа найдется свое делимое), истинное;
- высказывание “для всякого натурального числа найдется такое натуральное, которое делится на первое” (или для всякого натурального числа найдется свое делимое), истинное;
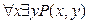 - высказывание “для всякого натурального x существует такое натуральное число y, на которое оно делится” (или «для всякого натурального числа найдется свой делитель»), истинное;
- высказывание “для всякого натурального x существует такое натуральное число y, на которое оно делится” (или «для всякого натурального числа найдется свой делитель»), истинное;
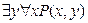 - высказывание “существует натуральное число, которое является делителем всякого натурального числа”, истинное (таким делителем является единица).
- высказывание “существует натуральное число, которое является делителем всякого натурального числа”, истинное (таким делителем является единица).
В общем случае изменение порядка следования кванторов изменяет смысл высказывания и его логическое значение, т.е. например, высказывания 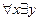 P(x,y) и
P(x,y) и 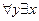 P(x,y) различны.
P(x,y) различны.
Пусть предикат P(x,y) означает, что x является матерью для y, тогда 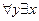 P(x,y) означает, что у каждого человека есть мать – истинное утверждение.
P(x,y) означает, что у каждого человека есть мать – истинное утверждение. 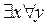 P(x,y) означает, что существует мать всех людей. Истинность этого утверждения зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, в противном случае оно ложно. Таким образом, перестановка кванторов всеобщности и существования может изменить сам смысл и значение выражения.
P(x,y) означает, что существует мать всех людей. Истинность этого утверждения зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, в противном случае оно ложно. Таким образом, перестановка кванторов всеобщности и существования может изменить сам смысл и значение выражения.
Квантор существования 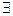 можно выразить через квантор всеобщности применительно к предикату P(x),
можно выразить через квантор всеобщности применительно к предикату P(x), 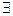 xP(x) =
xP(x) = 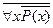
Квантор общности можно выразить с помощью квантора существования.
Пусть F1(x)= 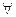 yP(x,y), тогда
yP(x,y), тогда 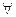 yP(x,y)=
yP(x,y)= 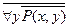 .
.
Операции над предикатами.Все формулы логики высказываний являются частным случаем логики предикатов. Все операции логики высказываний переносятся в логику предикатов.
Отрицание предиката. Чтобы образовать отрицание предиката, начинающегося одним из знаков 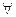 или
или 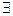 , можно:
, можно:
1) либо поставить знак  перед всем высказыванием
перед всем высказыванием
2) либо
а) заменить начальный знак ( 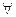 или
или 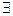 ) на противоположный
) на противоположный
б) поставить знак  перед остальной частью предиката
перед остальной частью предиката
Дата добавления: 2015-08-21; просмотров: 4819;
