Пример 4.
а) x – кошка, P(x) – у x есть усы. Усы есть у всех кошек 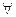 xP(x).
xP(x).
Найдется кошка без усов 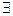 x
x 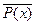 .
.
Не бывает кошек с усами; 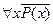 или
или 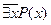 ;
;
б) x – человек, P(x) – x высокий, Q(x) – x толстый
Любой человек высокий и толстый 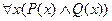
Найдется некто короткий и толстый 
Нет никого высокого и худого 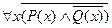 ,
, 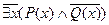
Найдется некто короткий и худой 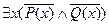 ,
, 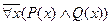
Таким образом, отрицаниемпредиката P(x) называется новый предикат 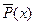 , который принимает значение “истина” при всех значениях
, который принимает значение “истина” при всех значениях 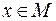 , при которых P(x) принимает значения “ложь” и наоборот. Здесь очевидно, I
, при которых P(x) принимает значения “ложь” и наоборот. Здесь очевидно, I 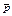 =M\Ip.
=M\Ip.
Конъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x) 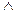 Q(x), который принимает значения “истина“ только при тех значениях x
Q(x), который принимает значения “истина“ только при тех значениях x 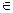 М, при которых каждый из предикатов принимает значения “истина“, и “ложь“ во всех остальных случаях. Область определения истинности предиката P(x)
М, при которых каждый из предикатов принимает значения “истина“, и “ложь“ во всех остальных случаях. Область определения истинности предиката P(x) 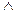 Q(x) – это Jp
Q(x) – это Jp 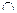 JQ.
JQ.
Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x) 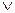 Q(x), который принимает значения “ложь” при тех и только тех значениях
Q(x), который принимает значения “ложь” при тех и только тех значениях 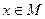 , при которых каждый из предикатов принимает значения “ложь”, и принимает значение “истина” во всех остальных случаях. Ясно, что IQ
, при которых каждый из предикатов принимает значения “ложь”, и принимает значение “истина” во всех остальных случаях. Ясно, что IQ  IP.
IP.
ИмпликациейP(x) и Q(x) называется новый предикат 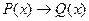 , который является ложным при тех и только тех значениях
, который является ложным при тех и только тех значениях 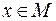 , при которых одновременно P(x) принимает значения “истина”, а Q(x) – значение ложь, и принимает истинное значение во всех остальных случаях.
, при которых одновременно P(x) принимает значения “истина”, а Q(x) – значение ложь, и принимает истинное значение во всех остальных случаях.
Эквиваленцией предикатов P(x) и Q(x) будет предикат  , который принимает значение «истина» только тогда, когда P(x) и Q(x) принимают одинаковые значения. Эти же правила справедливы и в случае, если рассматриваются не только одноместные предикаты.
, который принимает значение «истина» только тогда, когда P(x) и Q(x) принимают одинаковые значения. Эти же правила справедливы и в случае, если рассматриваются не только одноместные предикаты.
Пример 5. На множестве М={3,4,5,6,7,8} заданы два предиката P(x): “x – простое число“, Q(x): “x – нечетное число“. Составить их таблицы истинности. Равносильны ли предикаты P(x) и Q(x) на множествах L={2,3,4,5,6,7,8}, К={3,4,5,6,7,8,9}?
Таблица 2
| М | ||||||
| P(x) | ||||||
| Q(x) |
Очевидно, что Ip={3,5,7}, Iq={3,5,7}. Таким образом, на множестве М P(x)=Q(x) . На L и K предикаты не равносильны, ибо на множестве L, например, 2- число простое и четное, а на множестве К - число 9 – нечетное, но составное число.
Дата добавления: 2015-08-21; просмотров: 1730;
