Условная вероятность. Независимые и зависимые события. Теорема о вероятности произведения событий.

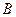Пусть и – события, которые могут наступить в результате стохастического эксперимента. Осуществим этот эксперимент n раз. Пусть 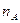– число опытов, в которых появилось событие , 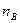– число опытов, в которых появилось событие 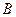, 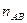– число опытов, в которых появились события и 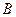одновременно. Условной частотой события при условии, что событие 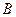произошло, называется частота события , вычисленная не по всем испытаниям, а только по совокупности тех испытаний, в которых событие 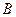произошло, т.е. .

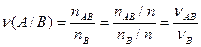Пусть задано вероятностное пространство 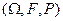, события 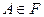, и .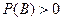

Тогда условная вероятность события при условии, что событие 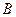произошло, равна

, (1)

где .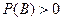

Аналогично определяется условная вероятность события 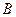при условии, что событие произошло

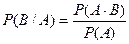, (2)

где .

Из формул (1) и (2) следует формулировка

теоремы о вероятности произведения событий (теоремы умножения вероятностей)

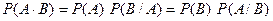
Эту формулу можно обобщить на случай произведения событий.

Пусть случайные события, для которых 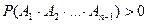. Учитывая, что 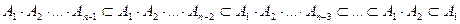, из условия 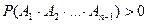получим 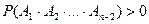, , 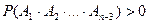…, , 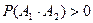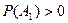. Следовательно, определены условные вероятности

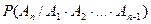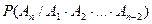, ,…, . Тогда

(3)

Эта формула доказывается методом математической индукции.

База индукции: при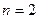

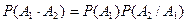. (4)

Предположим, что формула (3) справедлива для событий, т.е.

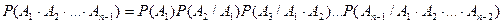
(5)

Обозначая 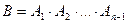, получим на основании (4)

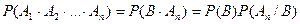(6)

Подставляя в (6) выражение для 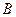и учитывая (5), получим (3).

Например, для трех событий формула (3) имеет вид

События и 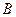называются независимыми, если наступление события не изменяет вероятности события 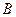, т.е.

.

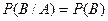Отсюда следует, что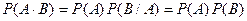

С другой стороны, 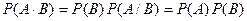. Следовательно,

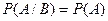, т.е. свойство независимости событий является взаимным.

Понятие независимости событий нельзя смешивать с понятием несовместности событий. Если и 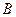- независимые события с положительными вероятностями, то они совместны.

Вероятность произведения независимых событий равна произведению вероятностей событий

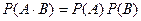
События называются независимыми в совокупности, если для любых 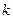из них ( 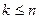) выполняется соотношение

, (7)

В частности

.

Если соотношение (7) выполняется для 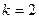, то события называются попарно независимыми.

Попарная независимость нескольких событий ещё не означает их независимость в совокупности.