Пример 3. Три стрелка независимо друг от друга стреляют по мишени
Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания для первого стрелка 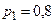 , для второго
, для второго  , для третьего
, для третьего 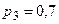 .
.
Найти вероятности событий
 – все трое попали в цель,
– все трое попали в цель,
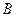 – хотя бы один из стрелков промахнулся,
– хотя бы один из стрелков промахнулся,
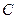 – попали два стрелка, один допустил промах,
– попали два стрелка, один допустил промах,
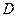 – хотя бы один стрелок попал в цель.
– хотя бы один стрелок попал в цель.
Решение .
Введём обозначения:
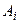 –
– 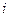 -ый стрелок попал в цель,
-ый стрелок попал в цель,  ;
;
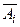 –
– 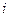 -ый стрелок не попал в цель,
-ый стрелок не попал в цель, 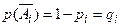 .
.
 можно представить в виде
можно представить в виде 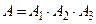 и по теореме о произведении вероятностей
и по теореме о произведении вероятностей 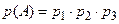 .
.
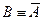 и по теореме о вероятности противоположного события
и по теореме о вероятности противоположного события 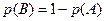 .
.
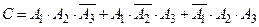 , т.е. является суммой несовместных слагаемых, и по теоремам о вероятностях суммы и произведения
, т.е. является суммой несовместных слагаемых, и по теоремам о вероятностях суммы и произведения

Вероятность события 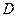 найдём двумя способами.
найдём двумя способами.
1). 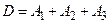 и
и
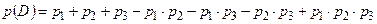 .
.
2).  и
и 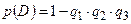 .
.
Ответ
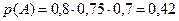
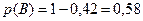
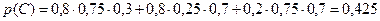
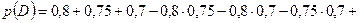
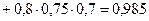 или
или
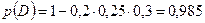 .
.
Дата добавления: 2015-08-21; просмотров: 1373;
