Свойства вероятностей событий

Из аксиом вероятностей

1)

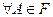
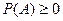
2) ,

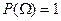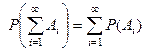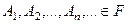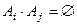3) , если . и при 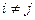для любых ,

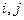можно вывести несколько свойств вероятностей, иногда называемых теоремами:

4) 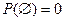, т.е вероятность невозможного события равна нулю.

Доказательство. 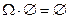, следовательно, события 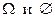несовместны, тогда , учитывая, что 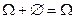, в соответствии с аксиомой 3) получим 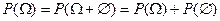. Следовательно, 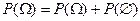, а значит вероятность невозможного события равна нулю: .

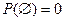5) Теорема о вероятности противоположного события

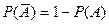
Доказательство. 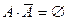, т.е. события и 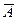несовместны. Тогда, учитывая, что 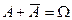, в соответствии с аксиомой 3) получим 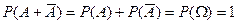, отсюда .

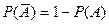6). Теорема о вероятности разности событий

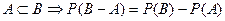
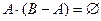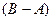Доказательство. , следовательно, и – несовместные события. Тогда, учитывая, что 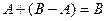, в соответствии с аксиомой 3) получим .

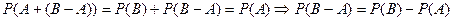7). .

Доказательство. и 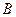– события. Следовательно, 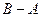– событие. В соответствии с аксиомой 1) 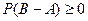. Тогда из свойства 6) следует 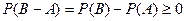. Отсюда .

8) . Для любого события справедливо неравенство .

Доказательство. 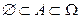. Тогда в соответствии со свойством 7) 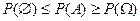. Учитывая, что 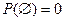, , 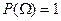получим .

9. Теорема о вероятности суммы совместных событий ( теорема сложения вероятностей).

Пусть 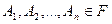. Тогда

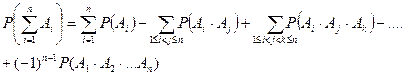(1)

Эту формулу можно записать иначе

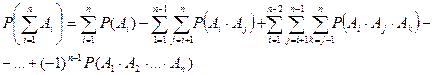
В частности, утверждение теоремы сложения вероятностей имеет следующий вид

для двух событий

;

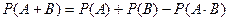для трех событий

.

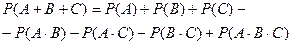Доказательство формулы (1) проводится методом математической индукции.

База индукции: пусть 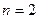. Докажем, что .

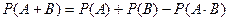События и 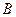несовместны. Действительно,

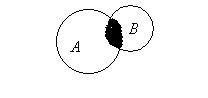
Тогда

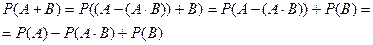
Отсюда

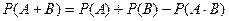(2)

Далее делается индукционное предположение, что формула (1) верна для произвольных событий 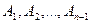. Обозначив 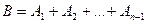, получим

.

Подставляя сюда известные выражения 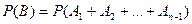и получим формулу (1).