Вероятностное пространство эксперимента с несчетным числом исходов

Для стохастических экспериментов с конечным и счетным числом исходов вводятся дискретные вероятностные пространства. Однако существует большое число стохастических экспериментов с несчетным числом исходов.

Например, 1)попадание в круг при стрельбе , множество исходов–точки круга (несчетное множество); 2) бросание точки на отрезок 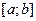, исходом является координата брошенной точки. Тогда множество исходов эксперимента несчётно. В этих случаях нельзя построить вероятностную модель эксперимента, приписав вероятности отдельным элементарным событиям. Действительно, если по аналогии с дискретным случаем задать для каждого исхода 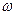вероятность 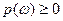, то сумма вероятностей по всем исходам 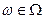, если число исходов несчетно, будет равна 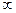, а, следовательно, не будет выполняться аксиома нормировки 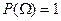. В этой ситуации вероятности приписывают не отдельным исходам, а множествам исходов, которые образуют события.

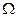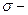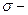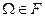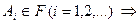
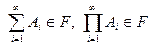Пусть имеется пространство элементарных событий эксперимента. Для этого пространства построим алгебру его подмножеств, которая как алгебра обладает свойствами 1) , 2) ; 3) .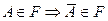

Множества, входящие в 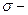алгебру называются событиями, а не входящие в нее, событиями не являются.

Вероятность события определим как числовую функцию 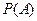, заданную на 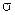-алгебре подмножеств пространства элементарных событий 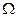и удовлетворяющую аксиомам вероятностей:

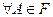
1) 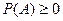(неотрицательности).

2) 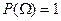, (нормированности) .

3) Если события 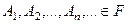и попарно несовместны, т.е. 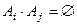при 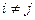для любых 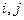, то

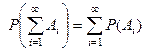-– свойство счетной аддитивности

Тройка 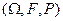называется вероятностным пространством иливероятностной моделью эксперимента.

Такая аксиоматика теории вероятностей была сформулирована А.Н. Колмогоровым в 1933 году. Она является универсальной, т.е. может быть использована для эксперимента с любым числом исходов.