Вероятностное пространство стохастического эксперимента со счетным числом исходов
Если множество элементарных исходов эксперимента счётно, то это множество исходов является пространством элементарных событий ,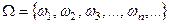 
, а любое его подмножество называется событиием. Из всех подмножеств множества 
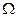строится 
– алгебра 
, на которой определяются операции суммы, произведения, разности и перехода к противоположному событию. Система всех подмножеств множества 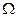обладает следующими свойствами:
1)) 
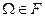, т.е. достоверное событие входит в .
2) замкнуто относительно счетного числа операций сложения и умножения событий, т.е.
если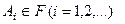 
, то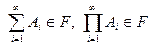 
3) 
.
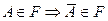Отсюда следует, что
4) 
, так как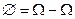 
;
5) 
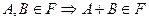
6) 
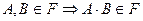
7) 
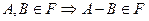
Каждому элементарному событию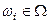 
(исходу эксперимента) аксиоматически приписывают число 
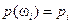, называемое вероятностью этого исхода, т.е. на 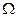задается числовая функция 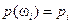, которая должна удовлетворять условиям:
1. 
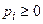для любого 
– аксиома неотрицательности;
2. 
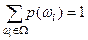(или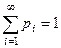 
) .– аксиома нормированности.
|
| 
| 
| … | 
| … |
| 
| 
| … | 
| … |
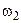
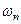
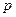
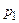
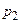
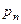
где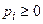 
; 
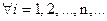Вероятность произвольного события 
определяется равенством
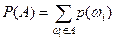
Функция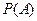 
определена на – алгебре и обладает свойствами, которые иногда называются аксиомами теории вероятностей
1) 
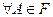
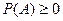(свойство неотрицательности).
2) 
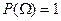, ( свойство нормированности)
3) Если события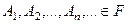 
и попарно несовместны, т.е. 
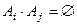при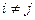 
для любых 
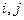, то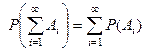 
-– свойство счетной аддитивности.
Следовательно, вероятность – неотрицательная, нормированная , счетно-аддитивная числовая функция, заданная на множестве .
Тройка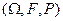 
определяет вероятностное пространство, соответствующее данному эксперименту.
Пример. Пусть симметричная монета бросается до тех пор, пока не появится герб. Найти вероятность того, что будет произведено не более трех бросаний.
Решение.
Пространство элементарных событий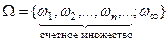 
, 
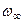означает, что герб не появится никогда. 
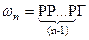. Припишем 
,
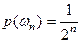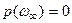(условие неотрицательности выполнено). Тогда 
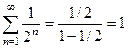, т.е. условие нормировки выполнено. Герб может появиться либо при первом, либо при втором, либо при третьем бросании. Поэтому 
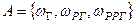и 
.
Дата добавления: 2015-08-21; просмотров: 1570;