Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена

Ищем приближающую функцию в виде:

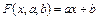. (7.11)

Находим частные производные

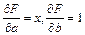. (7.12)

Составляем систему вида (7.8)

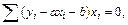
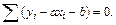
(Здесь и далее сумма ведется по переменной .)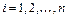

Далее имеем

,

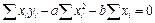(7.13)

Разделив каждое уравнение (7.13) на n, получаем

,

.

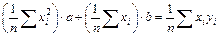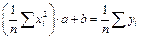Введем обозначения

.

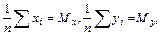
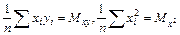Тогда последняя система будет иметь вид

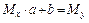
или в матричной форме

.

Откуда

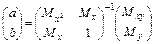. (7.14)

Вычислив значения параметров a, b в соответствие с (7.14), получаем конкретные значения и, следовательно, конкретный вид линейной функции (7.11).

В случае нахождения приближающей функции в форме квадратного трехчлена имеем:

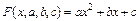. (7.15)

Находим частные производные:

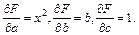
Составляем систему вида (7.8)

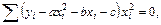
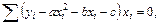
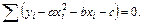
Далее имеем

,

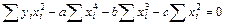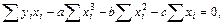
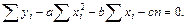
Разделив каждое уравнение на n и перенеся члены, не содержащие неизвестные параметры в правую часть получаем:

,

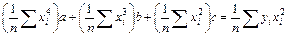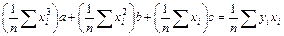, (7.16)

.

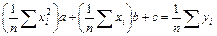Решив систему (7.16) относительно неизвестных a, b, c, находим значения параметров приближающей функции.

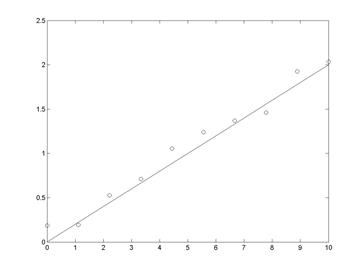
Рис. 7.2

Для нахождения решения задачи о нахождении линейного и квадратичного трехчленов в пакете MATLAB необходимо выполнить следующую последовательность команд:

% задание исходных данных

>> N=10;

>> i=1:N;

>> Xmin=0;

>> Xmax=10;

>> x(i)=Xmin+(Xmax-Xmin)/(N-1)*(i-1);

>> y(i)=0.2*x(i);% точные значения функции

% задание шума с равномерным законом распределения на

% отрезке [b,a]

>> a=0.2

>> b=-0.1;

>> Yrnd=b+(a-b)*rand(N,1);

>> y1=y+Yrnd'; % создание зашумленных данных

>> plot(x,y,x,y1,'o'); % визуализация точной и зашумленной

% последовательностей (рис. 7.2)

% вычисление элементов матрицы M в (7.14)

>> tmp=x(i).^2;

>> M(1,1)=1/N*sum(tmp);

>> M(1,2)=1/N*sum(x);

>> M(2,1)=M(1,2);

>> M(2,2)=1;

% вычисление элементов вектора d

>> d(1,1)=1/N*dot(x,y1);

>> d(2,1)=1/N*sum(y1);

% решение системы линейных уравнений (7.14)

>> Coeff=A^-1*d;

Coeff =

0.1941

0.0993

>> F=inline('a*x+b','a','b','x'); % задание аппроксимирующей

% функции

>> tmp1(i)=feval(F,Coeff(1,1),Coeff(2,1),x(i));% вычисление

% значений

% аппроксимирующей

% функции

% вычисление суммы квадратов отклонений

% при линейной аппроксимации

>> tmp=tmp1-y1;

>> dot(tmp,tmp)

ans =

0.0685

% аппроксимация исходных данных полиномом второй степени

% задание матрицы системы линейных уравнений в (7.16)

>> A(1,1)=1/N*sum(x.^4);

>> A(1,2)=1/N*sum(x.^3);

>> A(1,3)=1/N*sum(x.^2);

>> A(2,1)=A(1,2);

>> A(2,2)=A(1,3);

>> A(2,3)=1/N*sum(x);

>> A(3,1)=A(2,2);

>> A(3,2)=A(2,3);

>> A(3,3)=1;

% задание вектора столбца свободных членов

>> d(1,1)=1/N*dot(x.^2,y1);

>> d(2,1)=1/N*dot(x,y1);

>> d(3,1)=1/N*sum(y1);

% решение системы линейных уравнений (7.16)

>> Coeff=A^-1*d

Coeff =

0.0004

0.1904

0.1049

>> F=inline('a*x.^2+b*x+c','a','b','c','x'); % задание

% аппроксимирующей

% функции

% вычисление суммы квадратов отклонений при квадратичной

% интерполяции

>> tmp2(i)=feval(F,Coeff(1,1),Coeff(2,1),Coeff(3,1),x(i));

>> tmp=tmp2-y1;