Метод наименьших квадратов

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости (табл. 7.1).

Таблица 7.1

x			…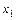
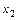
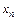
f(x)			…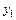

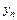
Требуется найти формулу, выражающую данную зависимость аналитически.

Один из подходов к решению данной задачи состоит в построении интерполяционного многочлена, значения которого будут в точках 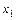, ,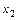…, 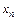совпадать с соответствующими значениями из табл. 7.1. Однако совпадение значений в узлах может вовсе не означать совпадения характеров исходной и интерполирующей функций. Требование неукоснительного совпадения значений, тем более неоправданно, если значения функций известны с некоторой погрешностью (рис. 7.1).

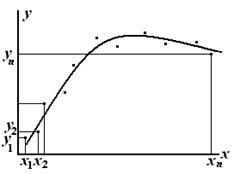
Рис. 7.1

Поставим задачу так, чтобы с самого начала обязательно учитывался характер исходной функции: найти функцию заданного вида

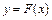,(7.1)

которая в точках 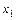, ,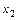…, 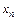принимает значения как можно более близкие к табличным значениям , ,…, .

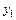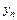Следует отметить, что строгая функциональная зависимость для табл. 7.1. наблюдается редко, т. к. каждая из входящих в нее величин может зависеть от многих случайных факторов, поэтому обычно используют простые по виду аналитические функции.

Рассмотрим один из наиболее распространенных способов нахождения функции 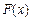. Предположим, что приближающая функция 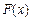в точках 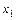, ,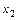…, 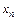имеет значения

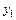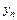, ,…, .(7.2)

Требование близости табличных значений 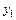, ,…, 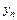и значений (7.2) можно истолковать следующим образом. Будем рассматривать совокупность значений функции из табл. 7.1 и совокупность значений (7.2) как координаты двух точек n-мерного пространства. С учетом этого задача приближения функции может быть переформулирована следующим образом: найти такую функцию 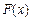заданного вида, чтобы расстояние между точкам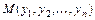и и 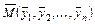было наименьшим. Воспользовавшись метрикой Евклидова пространства, приходим к требованию, чтобы величина

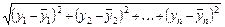, (7.3)

была наименьшей. Это равносильно следующему: сумма квадратов

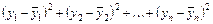(7.4)

должна быть наименьшей.

Таблица 7.2

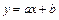
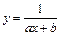
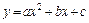
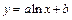
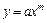
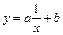
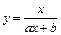
Окончательно задача приближения функции теперь формулируется следующим образом: для функции , заданной табл. 7.1, найти функцию 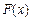определенного вида так, чтобы сумма квадратов (7.4) была наименьшей. Эта задача называется приближением функции методом наименьших квадратов. В качестве приближающих функций в зависимости от характера точечного графика функции часто используют функции, представленные в табл. 7.2. (Здесь a, b, m - неизвестные параметры)

Когда вид приближающей функции установлен, задача сводится к отысканию значений параметров.

Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции, зависящей от трех параметров:

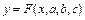.(7.5)

Имеем

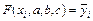, (7.6)

Сумма квадратов разностей соответствующих значений функций и 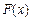имеет вид:

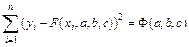. (7.7)

Сумма является функцией 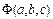трех переменных. Используя необходимое условие экстремума:

,

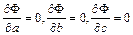получаем систему уравнений

,

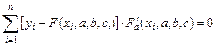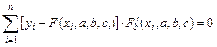, (7.8)

.

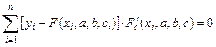Решив систему (7.8) относительно параметров a, b, c, получаем конкретный вид функции 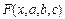. Изменение количества параметров не приведет к изменению сути самого подхода, а выразится в изменении количества уравнений в системе (7.8).