Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
С геометрической точки зрения определенный интеграл
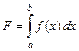 , (6.11)
, (6.11)
есть площадь фигуры, ограниченная графиком функции  и прямыми
и прямыми 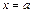 ,
, 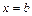 (рис. 6.3).
(рис. 6.3).

Рис. 6.3
Разделим отрезок 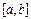 на N равных отрезков длиной
на N равных отрезков длиной  , где
, где
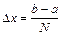 . (6.12)
. (6.12)
Тогда координата правого конца i-го отрезка определяется по формуле
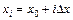 , (6.13)
, (6.13)
где 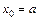 ,
, 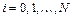 .
.
| 
|
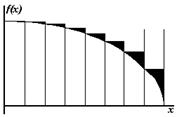
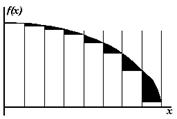
| Рис. 6.4. Метод левых прямоугольников | Рис. 6.5. Метод правых прямоугольников |
Простейшая оценка площади под кривой  может быть получена, как сумма площадей прямоугольников, одна из сторон которого совпадает с
может быть получена, как сумма площадей прямоугольников, одна из сторон которого совпадает с 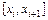 отрезком, а высота равна значению функции в точке
отрезком, а высота равна значению функции в точке 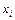 (метод левых прямоугольников) (рис. 6.4) или в точке
(метод левых прямоугольников) (рис. 6.4) или в точке 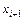 (метод правых прямоугольников) (рис. 6.5). (Погрешность вычисления значения интеграла на каждом шаге показана закрашенными фигурами.)
(метод правых прямоугольников) (рис. 6.5). (Погрешность вычисления значения интеграла на каждом шаге показана закрашенными фигурами.)
Значение определенного интеграла вычисляется по формулам
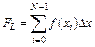 , (6.14)
, (6.14)
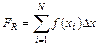 (6.15)
(6.15)
для методов левых и правых прямоугольников, соответственно.
Можно повысить точность вычисления определенного интеграла, если заменять реальную функцию на каждом интервале  ,
, 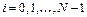 , отрезком прямой, проходящей через точки с координатами
, отрезком прямой, проходящей через точки с координатами 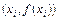 ,
, 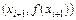 (линейная интерполяция).
(линейная интерполяция).
В этом случае фигура, ограниченная графиком функции и прямыми 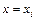 ,
, 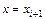 , является трапецией. Искомый определенный интеграл определяется как сумма площадей всех трапеций:
, является трапецией. Искомый определенный интеграл определяется как сумма площадей всех трапеций:
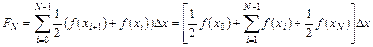 . (6.16)
. (6.16)
Более высокая точность вычисления интегралов обеспечивается при использовании параболической интерполяции (полиномом второй степени) по трем соседним точкам:
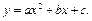 (6.17)
(6.17)
Более высокая точность вычисления интегралов обеспечивается при использовании параболической интерполяции (полиномом второй степени) по трем соседним точкам:
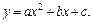 (6.17)
(6.17)
Для нахождения коэффициентов a, b, c полинома, проходящего через точки 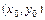 ,
, 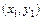 ,
,  , нужно найти решение следующей системы линейных уравнений:
, нужно найти решение следующей системы линейных уравнений:
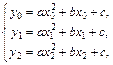 (6.18)
(6.18)
относительно неизвестных a, b, c.
Решив систему (6.18) относительно неизвестных a, b, c любым известным методом (например, Крамера), подставив найденные выражения в (6.17) и выполнив элементарные преобразования, получаем 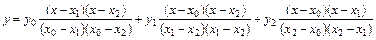 . (6.19)
. (6.19)
Площадь под параболой 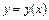 на интервале
на интервале 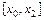 находится посредством элементарного интегрирования (6.19):
находится посредством элементарного интегрирования (6.19):
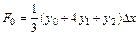 , (6.20)
, (6.20)
где 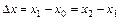 . Искомый определенный интеграл находится как площадь всех параболических сегментов (формула Симпсона):
. Искомый определенный интеграл находится как площадь всех параболических сегментов (формула Симпсона):
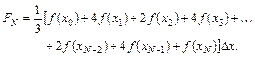 (6.21)
(6.21)
Обратите внимание на то обстоятельство, что в формуле Симпсона N должно быть четным числом.
Пример 6.2. Вычисление интеграла 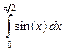 методом прямоугольников в пакете MATLAB:
методом прямоугольников в пакете MATLAB:
>> f=inline('sin(x)');% задание подынтегральной функции
>> Xmin=0;
>> Xmax=pi/2;
>> N=2001;
>> i=1:N;
>> dx=(Xmax-Xmin)/(N-1);% шаг интегрирования
>> x=Xmin:dx:Xmax; % вычисление координат узлов сетки
>> y=feval(f,x);% вычисление значений функции в узлах сетки
% вычисление интеграла по формуле правых прямоугольников
>> m=2:N;
>> y1(m-1)=y(m);
>> Fr=sum(y1)*dx
Fr =
1.0004
>> Fr-1
ans =
E-004
% вычисление интеграла по формуле левых прямоугольников
>> m=1:N-1;
>> y1(m)=y(m);
>> Fl=sum(y1)*dx
Fl =
0.9996
>> Fl-1
ans =
-3.9295e-004
% вычисление интеграла методом трапеций
>> s=0;
for i=2:N-1
s=s+y(i);
End;
Ft=(0.5*y(1)+s+0.5*y(N))*dx
Ft =
1.0000
>> Ft-1
ans =
-5.1456e-008
% вычисление интеграла методом Симпсона
>> s=0;
for i=2:N-1
if i-2*ceil(i/2)==0
k=4;
Else
k=2;
End;
s=s+k*y(i);
End;
Fs=(y(1)+s+y(N))*dx/3
Fs =
1.0000
>> Fs-1
ans =
E-015
Для вычисления значений определенных интегралов в пакете MATLAB имеются следующие функции quad( ), quadl( ), trapz( ), cumtrapz( ), которые имеют следующий синтаксис.
>> q = quad(fun,a,b)% возвращает значение интеграла от функции
% fun на интервале [a,b], при вычислении
% используется адаптивный метод Симпсона.
>> q = quad(fun,a,b,tol)% возвращает значение интеграла от
% функции fun с заданной относительной
% погрешностью tol (по умолчанию tol=10-3)
>> q = quad(fun,a,b,tol,trace)% возвращает значение интеграла от
% функции fun на интервале [a,b] на
% каждом шаге итерационного
% процесса
>> q = quad(fun,a,b,tol,trace,p1,p2,...)% возвращает значение
% интеграла от функции fun
% на на интервале [a,b] на
% каждом шаге
% итерационного процесса,
% p1, p2, … - параметры,
% передаваемые в функцию
% fun
>> [q,fcnt] = quadl(fun,a,b,...)% возвращает в переменную fcnt
% дополнительно к значению
% интеграла число выполненных
% итераций
Функция quadl( )возвращает значения интеграла, используя для вычислений метод Лоббато (Lobbato). Синтаксис функции аналогичен синтаксису функции quad( ).
q = quadl(fun,a,b)
q = quadl(fun,a,b,tol)
q = quadl(fun,a,b,tol, 'trace ')
q = quadl(fun,a,b,tol, 'trace ',p1,p2,...)
[q,fcnt] = quadl(fun,a,b,...)
Пример 6.3. Вычисление интеграла 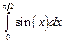 с использованием функций quad.
с использованием функций quad.
>> q=quad('sin',0,pi/2,10^-4)
q =
1.0000
>> q-1
ans =
-3.7216e-008
>> q=quad('sin',0,pi/2,10^-6,'trace');
E-001 0.0896208493
E-001 0.4966040522
E-001 0.2032723690
E-001 0.2933317183
E-001 0.4137750613
>> q-1
ans =
-2.1269e-009
>> [q,fnct]=quad('sin',0,pi/2,10^-6,'trace');
E-001 0.0896208493
E-001 0.4966040522
E-001 0.2032723690
E-001 0.2933317183
E-001 0.4137750613
>> 17
Функция trapz( ) вычисляет интеграл, используя метод трапеций. Синтаксис функции trapz( ):
Z = trapz(Y)% возвращает значение определенного интеграла, в
% предположении, что X=1:length(Y)
Z = trapz(X,Y)% возвращает значение интеграла
% на интервале [X(1),X(N)]
Z = trapz(...,dim)% интегрирует вектор Y, формируемый из чисел,
% расположенных в размерности dim
% многомерного массива
Функция cumtrapz( ) вычисляет интеграл, как функцию с переменным верхним пределом. Синтаксис функции cumtrapz( ) аналогичен синтаксису функции trapz( ).
Z = cumtrapz(Y)
Z = cumtrapz(X,Y)
Z = cumtrapz(... dim)
Пример 6.4. Вычисление определенного интеграла 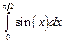 с использованием встроенной функции пакета MATLAB.
с использованием встроенной функции пакета MATLAB.
>> x=0:0.01:pi/2;% задание координат узловых точек
>> y=sin(x);% вычисление значений подынтегральной функции в
% узловых точках
>> trapz(y)% вычисление значения интеграла, в предположении о
% том, что шаг интегрирования равен единице
ans =
99.9195
>> trapz(x,y)% вычисление значения интеграла на отрезке 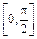 с
с
% шагом интегрирования 0.01
ans =
0.9992
Пример 6.5. Вычисление интеграла с переменным верхним пределом
>> x=0:0.01:3*pi/2;% задание координат узловых точек
>> y=sin(x);% вычисление значений подынтегральной функции в
% узловых точках
>> z=cumtrapz(x,y);% вычисление значений интеграла с
% переменным верхним пределом в узловых
% точках
>> plot(x,y,x,z)% построение графиков подынтегральной функции и
% интеграла с переменным верхним пределом
% (рис. 6.6)
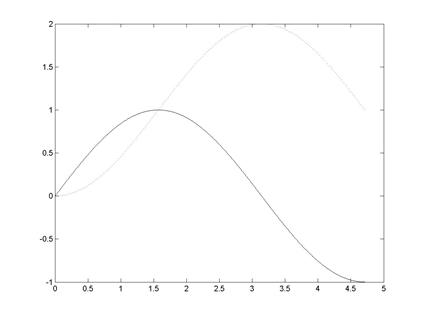
Рис. 6.6
Дата добавления: 2015-08-21; просмотров: 2677;
