Аналитически

По определению производная функции

. (6.1)

Переходя в (6.1) от бесконечно малых к конечным разностям, получаем приближенную формулу численного дифференцирования

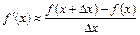. (6.2)

Формула (6.2) позволяет построить простой вычислительный алгоритм:

1) Задать значение точки, в которой вычисляется производная.

2) Задать значение приращение .

3) Вычислить производную в соответствие с формулой (6.2).

Замена бесконечно-малых приращений конечными является причиной возникновения ошибки. Для оценки ее величины разложим функцию в точке в ряд Тэйлора

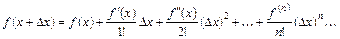(6.3)

Подставив (6.3) в (6.4) и приведя подобные члены, получим

. (6.4)

Из (6.4) видно, что все члены начиная с со второго, определяют отличие численного значения производной от ее точного значения. Основной член погрешности равен , т.к. данный член ~ , говорят, что формула (6.2) имеет первый порядок точности по .

Можно вычислять производную, используя симметричную разностную схему:

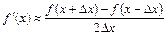. (6.5)

Для оценки точности данной формулы необходимо удержать в разложении в ряд Тэйлора первые четыре члена:

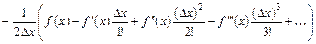. (6.6)

Раскрыв в (6.6) скобки и приведя подобные, получаем:

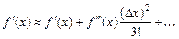. (6.7)

Из (6.7) видно, что основной член погрешности равен , т.к. данный член ~ , говорят, что формула (6.5) имеет второй порядок точности по .

Пример 6.1. Численное дифференцирование функции 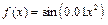в пакете MATLAB:

>> f=inline('sin(0.01*x.^2)');% задание дифференцируемой

% функции

>> dx=0.01; % шаг изменения координатной сетки

>> x=0:dx:10*pi; % вычисление координат узлов

>> yf=feval(f,x);% вычисление значений функции в узлах

% выполнение процедуры численного дифференцирования

>> N=length(x);

>> m=1:N-1;

>> df(m)=yf(m+1)-yf(m)

>> plot(df)% визуализация производной функции (рис. 6.1)

>> f1=inline('0.02*x.*cos(0.01*x.^2)');% задание функции,

% описывающей первую

% производную

>> ya=feval(f1,x);% вычисление значений первой производной по

% аналитической формуле

>> plot(x(m),abs(yf(m)-ya(m));% визуализация разности между

% численными и аналитическими

% значениями производной (рис. 6.2)

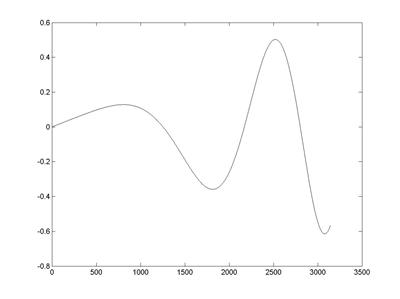
Рис. 6.1

Рис. 6.2

Аналогичным образом поступают при вычислении производных высших порядков.

Отметим, что для аппроксимации производных конечными разностями в пакете MATLAB имеется функция diff( ).

Синтаксис функции:

>> diff(X)% возвращает конечные разности, вычисленные по

% смежным элементам вектора Х длина вектора,

% возвращаемого функцией diff(X) на единицу

% меньше длины вектора Х, если X - матрица

%, то возвращает матрицу, содержащую

% конечные разности, вычисленные по каждому столбцу

>> diff(X,n) % возвращает конечные разности n-го порядка

>> diff(X,n,dim)% возвращает конечные разности n-го порядка по

% столбцам (dim=1) или строкам матрицы