Аналитические методы

Аналитические методы основаны на классических методах математического анализа.

Задача оптимизации формулируется следующим образом. Существует процесс, известна его математическая модель и установлен критерий оптимизации R в виде функции:

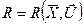(7.3)

Либо функционала:

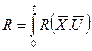(7.4), где: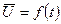

Заданы ограничения: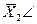

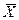
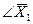
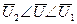
Необходимо при заданных ограничениях найти такие значения 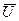, при которых Rдостигает экстремума. В случае функционала Кнеобходимо найти вид функции 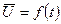, при которой Rдостигает экстремума.

Аналитические методы поиска экстремума критерия оптимальности применяются к задачам, у которых оптимизируемая функция имеет аналитическое выражение, а число переменных невелико.

В качестве примера рассмотрим определение оптимального времени пребывания смеси в РИВ.

W₁ W₂

Для двух последовательных реакций А -----> В------>Dнеобходимо определить оптимальное время пребывания t_опт, при котором выход целевого продукта В будет достигать максимума.

Пусть а– начальная концентрация компонента А.В начальный момент времени концентрации компонентов В и D равны нулю:

приt=0: C_В = С_D=0;

Критерий оптимизации: выход целевого продукта R=C_B/a.Управляющее воздействие – время пребывания t.

Характер изменения концентраций компонентов во времени приведен на рис. 7.2.

Пусть обе реакции протекают по первому порядку.

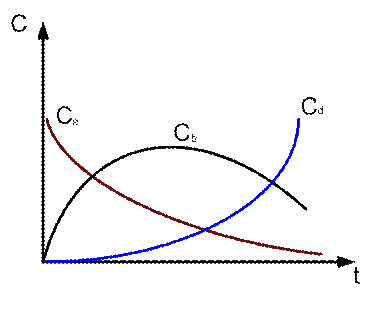
Рис. 7.2

W(1)=R(1)*WC(A) (7.5)

W(2)=K(2)*WC(B) (7.6)

dc(b)/dt=W1-W2 (7.7)

Из (7.5) найдем выражение для текущей концентрации С_А.

Преобразуем (7.5):

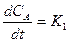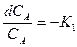- С_А; dt

Проинтегрировав, получим:

In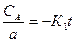(7.8)

Подставим (7.8) и (7.6) в (7.7):

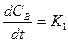ae^-K₁^t –K₂C_B

Или

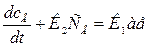
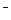
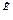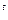₁(7.9)

Решив полученное уравнение, найдем выражение для определения текущей концентрации компонента В:

С_B=a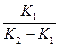(e^-^K₁^t - e^-^K₂^t)(7.10)

Выход целевого продукта:

R=C_B/a= 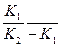(e^-K₁^t-e^-K₂^t)(7.11)

Исследуем экстремум полученной целевой функции (7.11). Условия существования максимума dR/dt=0; d²R/dt²<0; Найдем первую производную и приравняем ее нулю:

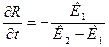(-K₁e^-^K₁^t-K₂e^-^K₂^t)=0 (7.12)

Решив полученное уравнение, определим оптимальное время пребывания:

t_opt=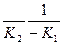In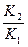(7.13)

Для проверки выполнения достаточного условия существования максимума вычисляем вторую производную:

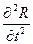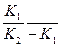=(K₁²e^-^K₁^t-K²₂e^-^K₂^t)<0

Так как вторая производная меньше 0, то в данной точке существует максимум целевой функции R. Подставив (7.13) в (7.10), получим выражение для определения максимальной концентрации компонента В:

C_B _opt= a²(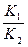) (7.14)

<12 131415 16 17 18 >

Дата добавления: 2015-08-26; просмотров: 1024;