Оптимизация химико-технологических процессов с использованием уравнения регрессии
Часто математической моделью процесса называют полученное эмпирическим путем уравнение, которое отражает количественную зависимость между параметрами процесса и имеет следующий вид:
Y=f(x1, x2, …xk), (7.20)
Уравнению (7.20), т.е. функции отклика, соответствует некоторая гиперповерхность в многомерном пространстве, называемом поверхностью отклика, пространство, в котором существует указанная поверхность, - факторным пространством. В простейшем случае, когда исследуется зависимость отклика от одного фактора поверхность отклика представляет собой линию на плоскости в двухмерном пространстве. В общем случае, когда рассматривается К факторов, уравнение (7.20) описывает поверхность отклика в (К+1)-мерном пространстве.
При весьма ограниченных знаниях о механизме процесса функцию отклика представляют в виде полинома ( уравнения регрессии)
Y=b0+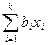 
+ 
+ 
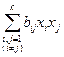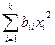+…(7.21)
где b0, bi, bij, bii - выборочные коэффициенты регрессии.
Так как степень полинома заранее предсказать нельзя, то сначала пытаются описать исследуемое явление самой простой линейной моделью. Далее проводят оценку ее качества - проверку модели на адекватность. Если результат оказался неудовлетворительным, повышают степень полинома, увеличивают число его членов и так до тех пор, пока не будет получена модель, адекватно описывающая результаты эксперимента. Проверка адекватности - статистическая процедура, выполняемая обычно с помощью F-критерия Фишера.
Математические модели, полученные при исследовании технологических объектов, позволяют решать ряд задач, например, осуществлять поиск оптимальных составов композиций, оптимальных условий работы исследуемого объекта (экстремальный эксперимент), проводимый с целью интенсификации производства, улучшения качества продукции.
Для получения математической модели объекта эксперименты обычно ставятся по заранее составленному алгоритму. Эта процедура называется планированием эксперимента.
По способу организации различают пассивное и активное экспериментирование. В первом случае объекты исследования наблюдают, результаты регистрируют и обрабатывают. Оценка свойств объекта в этом случае затруднена и осуществляется только по результатам многократных наблюдений. Более эффективным является целенаправленное изменение процесса и регистрации результатов, т.е. активное экспериментирование. Планировать можно только активный эксперимент.
Чтобы получить математическую модель, используют факторный эксперимент, суть которого заключается в варьировании всех факторов объекта исследования по определенному плану.
При планировании эксперимента необходимо учитывать требования к факторам и параметрам оптимизации. Важнейшими требованиями к факторам при постановке факторного эксперимента являются совместимость и некоррелированность. Совместимостьозначает, что внутри заданной области исследования практически осуществимы любые сочетания значений всех рассматриваемых факторов. Если же происходит нарушение режима работы изучаемого процесса, то такое сочетание факторов следует считать несовместимым, что требует изменения области определения уровней варьирования одного из факторов.
Требование некоррелированности (независимости) выдвигается для того, чтобы имелась возможность изменять значение каждого из факторов независимо друг от друга.
Поэтому перед осуществлением факторного эксперимента определяются: области существования факторов; число факторов и их взаимодействий, включаемых в план основного эксперимента; интервалы варьирования факторов; число параллельных опытов.
При планировании эксперимента предъявляются определенные требования и к параметрам оптимизации, выполнение которых необходимо для успешного решения задачи. Желательно, чтобы система во всей полноте характеризовалась небольшим числом параметров оптимизации, имеющих ясный физический смысл, что защищает экспериментатора от ошибок и упрощает технологическую интерпретацию полученных результатов.
Проверка соответствия входных и выходных параметров перечисленным требованиям осуществляется в ходе так называемого предварительного эксперимента.
Планирование эксперимента
1. Полный факторный эксперимент (ПФЭ).
При планировании по схеме ПФЭ реализуют все возможные комбинации факторов на всех выбранных для исследования уровнях.
Уровнем фактора называется определенное значение фактора, которое будет фиксироваться при проведении эксперимента.
Необходимое количество опытов при ПФЭ определяется по формуле:
N=Qk , (7.22)
где Q – количество уровней; к- количество факторов.
Как правило, ПФЭ организуется только на двух уровнях, которые представляют собой границы исследуемой области по данному технологическому параметру. При этом N=2k, а постановка опытов по такому плану называется полным факторным экспериментом типа 2к.
С увеличением количества факторов резко возрастает число опытов. В этом случае можно уменьшить объем экспериментальных работ, воспользовавшись дробным факторным экспериментом ДФЭ.
Этапы планирования, проведения и обработки результатов ПФЭ: кодирование факторов; составление план-матрицы эксперимента; рандомизация опытов; реализация плана-эксперимента; проверка воспроизводимости опытов; расчет коэффициента регрессии; оценка значимости коэффициента регрессии; проверка адекватности математической модели.
Кодирование факторов . Для облегчения статистической обработки математической модели уравнение регрессии (7.20) должно содержать безразмерные (кодовые) величины факторов. Переход от натуральных значений факторов (хi) к кодированным (хi) осуществляется по формуле
Xi=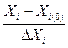 
(7.23)
где Хi – натуральное значение i-го фактора; Xi(0) – значение фактора на нулевом (среднем) уровне;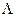 
Xi – интервал варьирования i-го фактора (разность между данным и средним значением фактора).
Например, при варьировании температуры в интервале 45÷55оС нижний (Хн) и верхний (Хв) уровни переменной равны
Хн=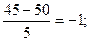 
Хв= 
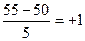
Удачный выбор интервала варьирования факторов гарантирует получение достоверной математической модели объекта.
Составление матрицы планирования эксперимента. План, содержащий запись всех комбинаций факторов (или их части для ДФЭ) в кодированной форме, называется матрицей планирования.
В табл. 7.1 и 7.2. представлены матрицы ПФЭ типа 22 и 23 и экспериментальные значения функций отклика; количество опытов рассчитывалось по формуле (7.22).
Таблица 7.1. Полный двухфакторный эксперимент
| Номер опыта | Факторы | Функция отклика | |
| Х1 | Х2 | ||
| +1 | +1 | У1 | |
| -1 | +1 | У2 | |
| +1 | -1 | У3 | |
| -1 | -1 | У4 |
Таблица 7.2. Полный трехфакторный эксперимент
| Номер опыта | Факторы | Функция отклика | ||
| Х1 | Х2 | Х3 | ||
| +1 | +1 | +1 | У1 | |
| -1 | +1 | +1 | У2 | |
| +1 | -1 | +1 | У3 | |
| +1 | +1 | -1 | У4 | |
| -1 | -1 | +1 | У5 | |
| -1 | +1 | -1 | У6 | |
| +1 | -1 | -1 | У7 | |
| -1 | -1 | -1 | У8 |
На практике необходимо учитывать парные взаимодействия факторов, для чего составляют расширенные матрицы (см.табл.7.3).
Чтобы искомая математическая модель в виде уравнения регрессии содержала наилучшие коэффициенты и точность предсказания значений функции отклика была одинакова по всем направлениям факторного пространства, матрица планирования ПФЭ должна удовлетворять условиям ортогональности и ротатабельности.
Условие ортогональности предполагает равенство нулю суммы произведений любых столбцов матрицы.
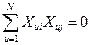(7.24)
где u – номер опыта; i, j – номера различных факторов (i≠ j).
Свойство ортогональности позволяет вычислять коэффициенты регрессии по простым формулам независимо друг от друга.
Ортогональные планы ПФЭ для линейных моделей имеют и свойство ротатабельности, которое предполагает равенство и минимальность дисперсий (отклонений), предсказанных значений функций отклика для всех точек факторного пространства.
Реализация плана эксперимента
После построения матрицы планирования приступают непосредственно к эксперименту. Чтобы матрица планирования имела вид, удобный для реализации, в ней представляют натуральные и кодированные значения факторов. Такую матрицу называют рабочей. Поскольку на изменение выходной переменной влияют помехи, план обычно реализуют несколько раз, получая несколько параллельных значений функции отклика.
Так как на систему могут оказывать влияние и другие факторы, не включенные в матрицу, необходимо внести элемент случайности влияния этих факторов на результат эксперимента, для чего устанавливается случайный порядок постановки опытов во времени. Эта процедура называется рандомизацией. Например, при реализации ПФЭ типа 23 опыты могут производиться в следующем порядке: 5,2,3,7,6,1,8,4.
Дата добавления: 2015-08-26; просмотров: 1564;