Постановка задачи оптимизации
Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация– целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно. Особенно большие трудности возникали при решении задач оптимизации процессов в химической технологии из-за большого числа параметров и их сложной взаимосвязи между собой. При наличии ЭВМ задача заметно упрощается.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
- количество продукции – расход сырья;
- количество продукции – качество продукции.
Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противостоящих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности.
В первом случае критерий оптимизации – производительность, а во втором –себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизирующего объекта. Объект должен обладать определенными степенями свободы – управляющими воздействиями.
3. Возможность количественной оценки оптимизирующей величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Как правило, формулировка задачи оптимизации включает:
1) выбор критерия оптимальности;
2) установление ограничений;
3) выбор оптимизирующих факторов;
4) запись целевой функции.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой – критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность). Однако в частых задачах оптимизации, когда объект является частью технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура). Например, устанавливается оптимальный температурный профиль, длительность цикла –«реакция-регенерация». Но в любом случае любой критерий оптимальности имеет экономическую природу.
Рассмотрим более подробно требования, которые должны предъявляться к критерию оптимальности.
1. Критерий оптимальности должен выражаться количественно.
2. Критерий оптимальности должен быть единственным.
3. Критерий оптимальности должен отражать наиболее существенные стороны процесса.
4. Желательно, чтобы критерий оптимальности имел ясный физический смысл и легко рассчитывался.
Любой оптимизируемый объект схематично можно представить следующим образом (рис. 7.1).
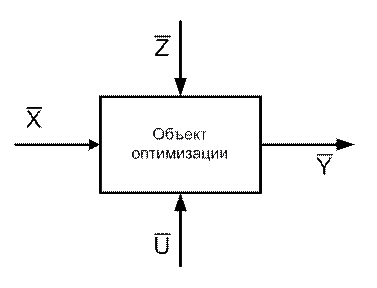
Рис. 7.1
| На рис. 7.1обозначено: |
| Y –выходы объекта; |
| X -контролируемые входные параметры; |
| U –регулируемые входные параметры, управляющие параметры; |
| Z –неконтролируемые воздействия. |
При постановке конкретных задач оптимизации критерий оптимальности должен быть записан в виде аналитического выражения. В том случае, когда случайные возмущения невелики, и их воздействие на объект можно не учитывать, критерий оптимальности может быть представлен как функция входных, выходных и управляющих параметров:
R=R(X1,X2…XN, Y1, Y2, …YN, U1, U2,…UN)(7.1)
Так как Y=f(U), то при фиксированных Х можно записать:
R=R(Ui)(7.2)
При этом всякое изменение значений управляющих параметров двояко сказывается на величине R:
- прямо, т.к. управляющие параметры непосредственно входят в выражение критерия оптимизации;
- косвенно– через изменение выходных параметров процесса, которые зависят от управляющих.
В принципе, для оптимизации вместо математической модели можно использовать и сам объект, однако оптимизация опытным путем имеет ряд существенных недостатков:
а) необходим реальный объект;
б) необходимо изменять технологический режим в значительных пределах, что не всегда возможно;
в) длительность испытаний и сложность обработки данных.
Наличие математической модели (при условии, что она достаточно надежно описывает процесс) позволяет значительно проще решить задачу оптимизации аналитическим либо численным методами.
В задачах оптимизации различают простые и сложные критерии оптимизации. Критерий оптимальности называется простым, если требуется определить экстремум целевой функции без задания условий на какие-либо другие величины. Такие критерии обычно используются при решении частных задач оптимизации (например, определение максимальной концентрации целевого продукта, оптимального времени пребывания реакционной смеси в аппарате и т.п.). Критерий оптимальности называется сложным, если необходимо установить экстремум целевой функции при некоторых условиях, которые накладываются на ряд других величин (например, определение максимальной производительности при заданной себестоимости, определение оптимальной температуры при ограничениях по термостойкости катализатора и др.).
Процедура решения задачи оптимизации обязательно включает, помимо выбора управляющих параметров, еще и установление ограничений на эти параметры (термостойкость, взрывобезопасность, мощность перекачивающих устройств). Ограничения могут накладываться как по технологическим, так и по экономическим соображениям.
Итак, для решения задачи оптимизации необходимо:
а) составить математическую модель объекта оптимизации:
Y=f(X,U)
б) выбрать критерий оптимальности и составить целевую функцию:
R=φ(Y)=F(X,U)
Целевая функция – это то же самое, что критерий оптимальности, но это критерий, рассматриваемый как функция входных факторов.
в) установить возможные ограничения, которые должны накладываться на переменные:
φi (X, U) = 0
Дата добавления: 2015-08-26; просмотров: 1554;
