Решение задачи одномерной интерполяции средствами пакете MATLAB

Для решения задачи одномерной сплайн-интерполяции в пакете MATLAB используется функция interp1( ), имеющая следующий синтаксис:

yi = interp1(x,y,xi)% линейная интерполяция табличных значений

% x,y в точках, абсциссы которых находятся

% в векторе xi

yi = interp1(y,xi)% линейная интерполяция табличных значений y

% в точках, абсциссы которых находятся

% в векторе xi,

% в предположении, что x=1:length(y)

yi = interp1(x,y,xi,method)% интерполяция линейных значений с

% использованием выбранного метода

% интерполяции

Возможные значения переменной method:

'nearest' % интерполяция с использованием ближайших узлов

'linear'% линейная интерполяция (по умолчанию)

'spline'% интерполяция кубическим сплайном

'pchip'% интерполяция полиномами Эрмита третьей степени

'cubic' % аналогично pchip

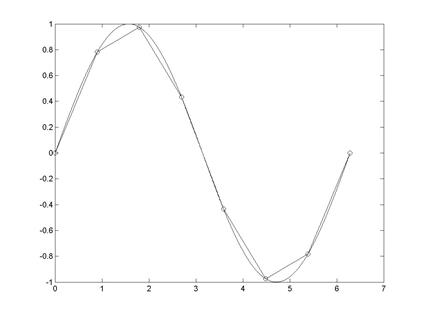
Рис. 5.10

Пример 5.1. Решение задачи интерполяции функции, заданной таблично средствами пакета MATLAB

1. Задание табличных значений интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Задание значения абсцисс точек, в которых вычисляется значение интерполяционного полинома

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X); % вычисление точных значений интерполируемой

% функции

4. Вычисление интерполируемых значений функции в узлах координатной сетки и визуализация точного исходных данных, точных и интерполированных значений % рис. 5.10

>> yi=interp1(x,y,X);

>> plot(x,y,'o',X,Y,X,yi)