Первая интерполяционная формула Ньютона

Будем искать интерполяционный полином в виде:

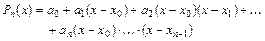. (5.15)

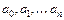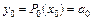Значения коэффициентов найдем из условия совпадения значений исходной функции и многочлена в узлах. Полагая , из (5.15) найдем , откуда 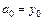. Далее последовательно придавая х значения 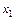и 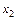, получаем:

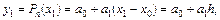
откуда ;

,

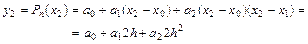т. е.

,

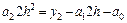или

,

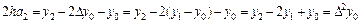откуда

.

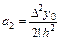Затем, проведя аналогичные выкладки, можно получить

.

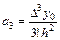В общем случае выражение для 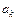будет иметь вид

. (5.16)

Подставляя (5.16) в выражение для многочлена (5.15), получаем

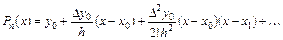
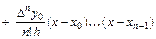(5.17)

Решение задачи о нахождении значений интерполяционного полинома находится в пакете MATLAB выполнением следующей последовательности действий.

1. Создать файл Newton1.m, содержащий описание функции, возвращаю­щей локальное значение интерполяционного полинома Ньютона

% листинг файла Newton1.m

function z=Newton1(t,x,y)

% t - абсцисса точки, в которой вычисляется значение интерполяционного

% полинома

% x, y - координаты точек, заданных таблично

N=length(x);

for i=1:N

f(i,1)=y(i);

End;

for k=2:N

for i=1:N-k+1

f(i,k)=(f(i+1,k-1)-f(i,k-1))/(x(i+k-1)-x(i));

End;

End;

s=y(1);

for k=2:N

r=1;

for i=1:k-1

r=r.*(t-x(i));

End;

s=f(1,k)*r+s;

End;

z=s;

2. Задать табличные значения интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

3. Задать значения абсцисс точек, в которых вычисляется значение интерполяционного полинома

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X); % вычисление точных значений интерполируемой функции

4. Вычислить значения полинома Ньютона в узлах заданной координатной сетки

>> for k=1:M

Z(j)=Newton1(X(j),x,y);

End;

5. Построение разности между точным и интерполированными значениями функции (рис. 5.4)

>> plot(X,Y-Z)

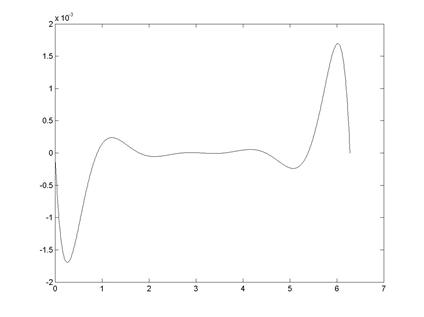
Рис. 5.4. Разность между точным и интерполированными значениями функции с помощью первого полинома Ньютона

Отдавая дань традициям преподавания численных методов, применявшимся в прошлом веке, приведем описание модификации формулы (5.17), применявшуюся при ручных вычислениях. Положим , т.е. 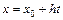, тогда:

,

,

…

.

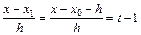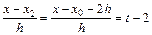Подставляя данные выражения в (5.17), окончательно получаем

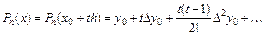
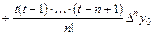. (5.18)

Формула (5.18) называется первой интерполяционной формулой Ньютона. Данная формула применяется для интегрирования в начале отрезка, когда t мало по абсолютной величине.