Постановка задачи. Пусть известные значения некоторой функции f(x)образуют следующую таблицу:

Пусть известные значения некоторой функции f(x)образуют следующую таблицу:

Таблица 5.1

Требуется получить значение функции f(x) для значения аргумента xÎ[x₀,x_n], несовпадающего ни с одним из значений х_i (i = 0, 1,.., n).

Решение задачи находится отысканием некоторой приближающей функции F(x), близкой в некотором смысле к функции f(x), для которой известно аналитическое выражение/

Классический подход к решению задачи построения приближающей функции основан на требовании строгого совпадения значений функций f(x)и F(x) в точках

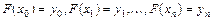. (5.1)

В данном случае нахождение приближенной функции называется интерполированием, а точки 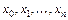называются узлами интерполяции.

Будем искать интерполирующую функцию F(x) в виде многочлена степени n:

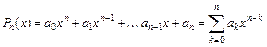. (5.2)

Условия (5.1), наложенные на многочлен, позволяют однозначно определить его коэффициенты. Действительно, требуя для 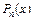выполнения условий (5.1), получаем линейную систему, состоящую из 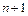уравнения:

. (5.3)

Решив систему (5.3) относительно неизвестных 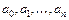, находим значения этих неизвестных и, подставив в (5.2), находим аналитическое выражение аппроксимирующей функции.

Система (5.3) всегда имеет единственное решение, т. к. ее определитель

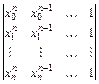, (5.4)

известный в алгебре как определитель Вандермонда, отличен от нуля.

Следовательно, интерполяционный многочлен 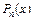существует и единственен.

Решение задачи интерполяции в пакете MATLAB с помощью полинома n-ой степени находится выполнением следующей последовательности команд:

1. Задать табличные значения интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Выполнить визуализацию табличной зависимости и истинных значений функции (рис. 5.1)

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X);

>> plot(x,y,'o');

>> hold on

>> plot(X,Y)

Рис. 5.1

3. Создать файл Pol.m, содержащего описание функции, возвращающей значения полинома (5.2)

% листинг файла Pol.m

function z=Pol(x,a)

N=length(a);

M=length(x);

for j=1:M

s=0;

for i=1:N

s=s+a(i)*x(j).^(N-i);

End;

z(j)=s;

End;

4. Создать файл Vandermod.m, содержащий описание функции, возвращающей значения элементов матрицы Вандермонда

% листинг файла Vandermond.m

function z=Vandermond(x)

N=length(x);

z=ones(N,N);

for i=1:N

for j=1:N

z(i,j)=x(i).^(N-j);

End;

End;

5. Вычислить значения элементов матрицы Вандермонда

>> M=Vandermond(x);

6. Вычислить значения коэффициентов полинома

>> a=M^-1*y';

7. Вычислить значения полинома в заданных промежуточных точках

>> Y1=Pol(X,a);

8. Построить разность между точным и интерполированными значениями функции (рис. 5.2)

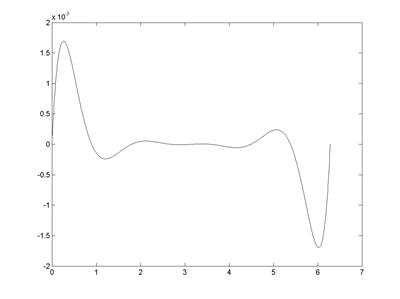
Рис. 5.2. Погрешность аппроксимации функции sin(x) полиномом 8-й степени