Relative function value changing by less than OPTIONS.TolFun. Рассмотрим реализацию метода спуска средствами пакета MATLAB на примере рассмотренной выше в настоящем разделе системе нелинейных уравнений

Рассмотрим реализацию метода спуска средствами пакета MATLAB на примере рассмотренной выше в настоящем разделе системе нелинейных уравнений. Напомним, что для этого, следуя подходу, описанному в разделе 4.3, нужно из уравнений исходной системы создать новую положительно определенную функцию, минимум которой и будет искомым решением системы нелинейных уравнений. Следовательно, для нахождения решения рассматриваемой системы нелинейных уравнений необходимо выполнить следующую последовательность действий:

1. Создать файл F_sq.m, содержащий описание функции, возвращающей значения суммы квадратов функций 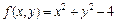и

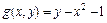
% листинг файла F_sq.m[2]

function z=F_sq(x)

s=fm(x);

z=s(1,1).^2+s(2,1).^2;

2. Задать начальное приближение, в окрестности которого будет находиться минимум функции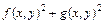

>> x=[1;1];

3. Обратиться к встроенной функции fminsearch( )

>> fminsearch('F_sq',x)

ans =

0.8896

1.7913

Отметим, что способы обращения к функции fminsearch( )и список ее формальных параметров аналогичны способам обращения к функции Fsolve( ) и списку ее формальных параметров.

ЛЕКЦИЯ № 5. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

План

5.1. Постановка задачи

5.2. Интерполяционный полином Лагранжа

5.3. Интерполяционный полином Ньютона для равноотстоящих узлов

5.3.1. Конечные разности

5.3.2. Первый интерполяционный полином Ньютона

5.3.3. Второй интерполяционный полином Ньютона

5.4. Погрешность метода многочленной интерполяции

5.5. Сплайн-интерполяция

5.6. Решение задачи одномерной интерполяции средствами пакете MATLAB