Function
z=g2_xx(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=12*Kx*x(i).^2+6*Lx*x(i)+2*Ox...
+12*Kxy*x(i).^2*y(j).^4+6*Lxy*x(i).*y(j).^3+2*Oxy*y(j).^2;
End;
End;
% листинг файла g2_xy.m
Function
z=g2_xy(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=16*Kxy*x(i).^3*y(j).^3+9*Lxy*x(i).^2*y(j).^2+…
4*Oxy*x(i).*y(j)+Pxy;
End;
End;
% листинг файла g2_yy.m
Function
z=g2_yy(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=12*Ky*y(j).^2+6*Ly*y(j)+2*Oy+...
12*Kxy*x(i).^4*y(j).^2+6*Lxy*x(i).^3*y(j)+2*Oxy*x(i).^2;
End;
End;
7. Создание файла Lambda2.m, содержащего описание функции, возвращающей значения коэффициента l
% листинг файлам Lambda2.m
Function
z=Lambda2(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
a1=g2_x(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).*...
S2_x(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);
a2=g2_y(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).*...
S2_y(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);
b1=g2_xx(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).*...
S2_x(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).^2;
b2=2*g2_xy(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)*…
S2_x(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).*...
S2_y(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);
g3=g2_yy(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).*...
S2_y(x(i),y(j),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy).^2;
z(i,j)=-(a1+a2)./(b1+b2+b3);
End;
End;
8. Создание файла MG2.m, содержащего описание функции, возвращающей значения переменных x,y и соответствующее значение функции f(x,y,m) на каждом шаге итерационного процесса
% листинг файла MG2.m
function [X,Y,ff]=MG(x0,y0,nu,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)
X(1)=x0;
Y(1)=y0;
ff(1)=F2_L4(x0,y0,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);
for i=2:nu
X(i)=X(i-1)+Lambda2(X(i-1),Y(i-1),Lx,Ly,Ox,Px,Lxy,Oxy,Q,…
Kx,Ky,Oy,Py,Kxy,Pxy)*s2_x(X(i-1),Y(i-1),Lx,Ly,Ox,Px,Lxy,Oxy,… Q,Kx,Ky,Oy,Py,Kxy,Pxy);
Y(i)=Y(i-1)+Lambda2(X(i-1),Y(i-1),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,… Ky,Oy,Py,Kxy,Pxy)*s2_y(X(i-1),Y(i-1),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,… Oy,Py,Kxy,Pxy);
ff(i)=F2_L4(X(i),Y(i),Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);
End;
9. Нахождение минимума функции f(x,y) и визуализация итерационного процесса
>> x0=1;y0=0.5;% начальное приближение
>> nu=10;% число шагов итерационного процесса
>>[X Y ff]=MG2(x0,y0,nu,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,… Kxy,Pxy);
>> plot(X); hold on; plot(Y); hold off% рис. 4.11
>> plot(ff);% рис. 4.12
>> stairs(X,Y);% рис. 4.13
>> plot3(X,Y,ff);% рис. 4.14
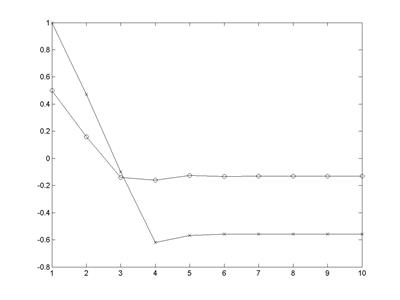
Рис. 4.11. Зависимость координат точки решения от номера итерации
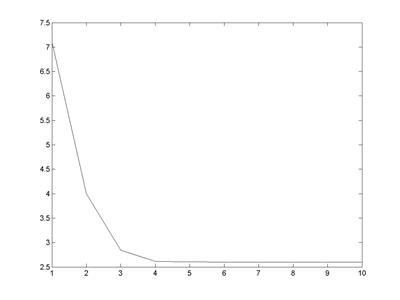
Рис. 4.12. Зависимость значения исследуемой функции от номера итерации
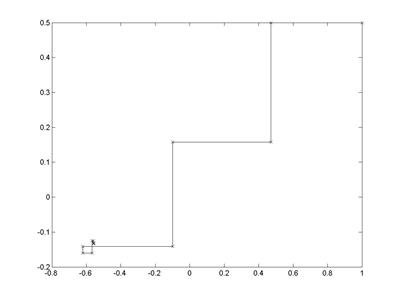
Рис. 4.13. Траектория итерационного процесса в плоскости XoY
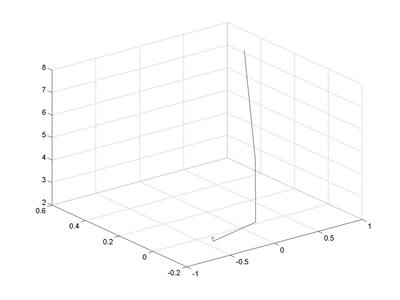
Рис. 4.14. Траектория итерационного процесса в пространстве
Обратите внимание на чрезвычайно быструю сходимость и на отсутствие колебаний решения. Это достигается за счет того, что формула для шага строится с учетом формы минимизируемой функции.
Из графика, представленного на рис. 4.10, видно, что функция имеет очень пологое «дно», поэтому для алгоритмов с шагом, не зависящим от формы функции, это было бы причиной очень плохой сходимости.
Метод Ньютона основан на квадратической аппроксимации минимизируемой функции в окрестности точки x(k). Минимум квадратической функции легко найти, приравнивая ее градиент нулю. Можно сразу же вычислить положение экстремума и выбрать его в качестве следующего приближения к точке минимума.
Вычисляя точку нового приближения по формуле: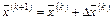 
и разлагая 
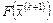в ряд Тейлора, получим формулу квадратической аппроксимации 
:
,
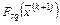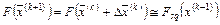где
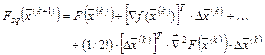, (4.21)
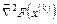– матрица вторых производных
.
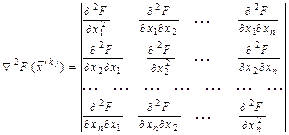Условие минимума 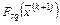по 
: 
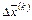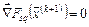. Вычислим градиент 
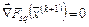из (4.22) и найдем значение :
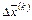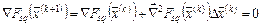. (4.22)
Для учета фактических особенностей минимизируемой функции будем использовать в (4.22) значения градиента и матрицы вторых производных, вычисленных не по аппроксимирующей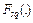 
, а непосредственно по минимизируемой функции 
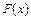. Заменяя 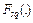в (4.22), найдем длину шага :
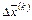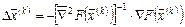. (4.23)
Метод Ньютона реализуется следующей последовательностью действий:
1. Задать (произвольно) точку начального приближения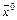 
.
2. Вычислять в цикле по номеру итерации k=0,1,…:
a) значение вектора градиента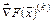 
в точке 
;
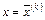b) значение матрицы вторых производных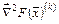 
;
c) значение матрицы обратной матрице вторых производных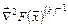 
;
d) значение шага 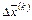по формуле (4.23);
e) новое значение приближения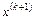 
по формуле (4.19).
3. Закончить итерационный процесс, используя одно из условий, описанных в п 1.5.
Достоинства метода Ньютона:
1. Для квадратической функции метод позволяет найти минимум за один шаг.
2. Для функций, относящихся к классу поверхностей вращения (т.е. обладающих симметрией), метод также обеспечивает сходимость за один шаг (поскольку в точке минимума аргументы минимизируемой функции и ее квадратической аппроксимации совпадают).
3. Для несимметричных функций метод обеспечивает более высокую скорость сходимости, чем при использовании других модификаций метода наискорейшего спуска.
К недостаткам метода Ньютона следует отнести необходимость вычислений и (главное!) обращения матриц вторых производных. При этом не только расходуется машинное время, но, что более важно, могут появиться значительные вычислительные погрешности, если матрица 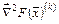окажется плохо обусловленной (т.е. значение определителя этой матрицы будет близко к нулю).
Пример 4.3. Поиск минимума функции Розенброка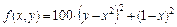 
методом, в котором шаг, зависит от свойств минимизируемой функции (метод Ньютона).
1. Создание файла Rozenbrok.m, содержащего описание функции, возвращающей значения функции Розенброка
% листинг файла Rozenbrok.m
function z=Rozenbrok(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=100*(y(j)-x(i).^2).^2+(1-x(i)).^2;
End;
end;
2. Задание координатной сетки
N=23; % число узлов сетки
i=1:N; j=1:N;
Xmin=-0.2; Xmax=1.2;
Ymin=-0.2; Ymax=1.2;
x(i)=Xmin+(Xmax-Xmin)/(N-1)*(i-1);
y(j)=Ymin+(Ymax-Ymin)/(N-1)*(j-1);
3. Вычисление значений функции в узлах координатной сетки
>> z=Rozenbrok(x,y);
4. Визуализация функции Розенброка и карты линий уровня
>> [X Y]=meshgrid(x,y);
>> surf(X,Y,z);% рис. 4.15
>> contour(X,Y,z,53) % рис. 4.16
5. Создание файла R_x.m, содержащего описание функции, возвращающей значение первой производной по переменной x
% листинг файла R_x.m
function z=R_x(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=-400*(y(j)-x(i).^2).*x(i)-2*(1-x(i));
End;
End;
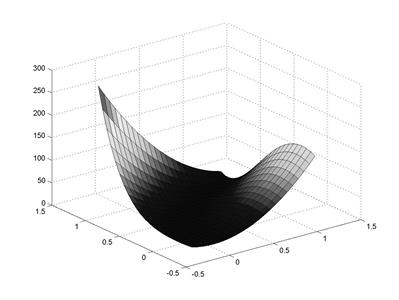
Рис. 4.15
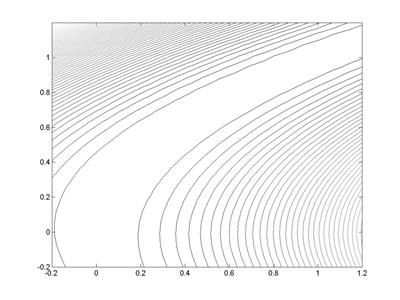
Рис. 4.16
6. Создание файла R_y.m, содержащего описание функции, возвращающей значение первой производной по переменной y
% листинг файла R_y.m
function z=R_y(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=200*(y(j)-x(i).^2);
End;
End;
7. Создание файла R_xx.m, содержащего описание функции, возвращающей значение второй производной по переменной x
% листинг файла R_xx.m
function z=R_xx(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=1200*x(i).^2-400*y(j)+2;
End;
End;
8. Создание файла R_yy.m, содержащего описание функции, возвращающей значение второй производной по переменной y
% листинг файла R_yy.m
function z=R_yy(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=200;
End;
End;
9. Создание файла R_xy.m, содержащего описание функции, возвращающей значение смешанной производной по переменным x, y
% листинг файла R_xy.m
function z=R_xy(x,y)
N=length(x);
z=zeros(N);
for i=1:N
for j=1:N
z(i,j)=-400*x(i);
End;
End;
10. Создание файла Rg.m, содержащего описание функции, возвращающей значения обратной матрицы вторых производных на вектор-градиент
% листинг файла Rg.m
function z=Rg(x,y)
A(1,1)=R_xx(x,y);
A(1,2)=R_xy(x,y);
A(2,1)=R_xy(x,y);
A(2,2)=R_yy(x,y);
B(1,1)=R_x(x,y);
B(2,1)=R_y(x,y);
z=A^-1*B;
11. Создание файла Rn0.m, содержащего описание функции, возвращающей значения переменных и соответствующих значений функции Розенброка
% Листинг файла Rn0.m
function z=Rg(x,y)
A(1,1)=R_xx(x,y);
A(1,2)=R_xy(x,y);
A(2,1)=R_xy(x,y);
A(2,2)=R_yy(x,y);
B(1,1)=R_x(x,y);
B(2,1)=R_y(x,y);
z=A^-1*B;
12.Визуализация итерационного процесса (рис. 4.17-4.19)
>> plot(x,'-x');
>> hold on
>> plot(y,'-o');
>> hold off
>> plot(z,'-o')
>> plot3(x,y,z,'-o'); grid on
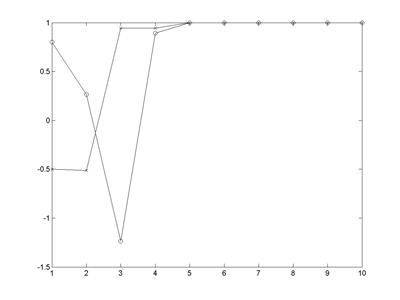
Рис. 4.16. Зависимость значений координат решения уравнения от номера итерации
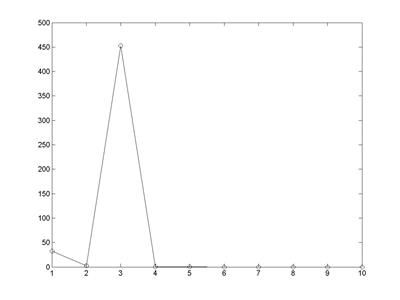
Рис. 4.17. Зависимость значения исследуемой функции в от номера итерации
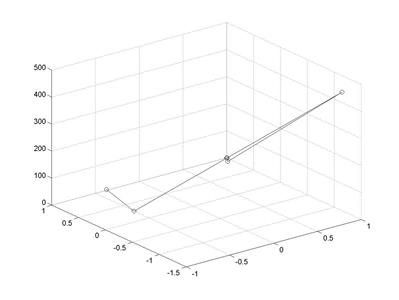
Рис. 4.18. Траектория итерационного процесса в пространстве
Дата добавления: 2015-08-21; просмотров: 839;